• 广度优先遍历解决迷宫问题

     前言:

            我们之前使用深度优先遍历的方法是 , 只派一个人去探索迷宫,记录其路线 和每个节点走过的方向 , 一条道走到黑 , 当路不通时候,回溯到上一个节点 的下一个方向 , 直到这个节点全部方向都遍历完,我们就放弃路线上的这个节点 ,接着回溯到这个节点的上一个节点的另一个方向 , 我们一定可以成功 ,因为我们就算不成功,早晚也可以回溯到起点 ,从起点的下一个方向出发 ,当把所有节点所有方向都遍历完,如果有解, 我们则可以找到出口 , 无解则输出无解 . 

    这种方法 ,有两个弊端,一个好处 ,好处就是 ,不耗费存储空间 ,我们一直都是在一个栈里进行反复的弹压元素 ,

    弊端就是我们反复回溯,耗费时间 , 并且我们所寻找的路线不一定是最佳路线,不是最短路线 ,我们可能一开始就不在最佳路线上,然后通过回溯,后续到了最佳路线中一个节点 , 然后到达终点 ,尽管我们成功了,但是我们第一时间没有在最佳路线上. 

           广撒网 ,团结就是力量  (深度优先遍历)

    看了前面的单人冒险 ,的确让我们捉急 , 我们现在增大我们的团队实力 ,变成孙悟空 ,拔一根猴毛 ,即可变出猴子 , 前往分岔路口的不同方向 , 只要人够多 ,我们就可以到达终点 ,并且最优路线是最短的 ,我们的探索人数够多 ,只要有解 ,就一定能够在最短的时间, 去到达最优路线 .一旦到达终点 ,我们即可吹一口仙气 ,把孩儿们收回来,探索成功. 

    我们现在用人脑来模拟一遍, 团队探索的过程:

    第一步: 我们从(1,1)出发 ,  标号① ,孙悟空真身到达现场

     注意: 标号行列 ,(行 , 列)

    第二步:  从①(1,1) 出发 , 我们遇到了两个方向 , 拔下猴毛,变成两个猴子,分别到(2,1) , (1,2) ,标号② (记作 标号记作第二次变身)

     第三步: 我们让二号变身猴开始走迷宫 ,我们现在又发现一个问题 ,两个②号猴同时走的话 ,会在(2,2)  相遇 ,我们怎么判断是哪一个路线上的猴子呢? 

    我们此时仿佛遇到了瓶颈, 当两个路线的猴子,都在 (2,2)相遇的时候 ,我们需要判断是哪个路线上的猴子吗? 或者存储他们的信息吗? 方便后续寻找路线? 

    引论:

    我们现在要找的是 长度最短 ,寻找用时最少的 最优路线 ,就像我们"黄河之水天上来,奔流到海不复回" , 两个路线汇合 ,这个说明两个路线都可以到达此(2,2)处

    我们看一下最终的图解路线:

    (2,1)和(1,2)处的分身② ,进行第三次分身 到了(3,1),(2,2) ,标号为③

    假如此时的目标地点是(3,2) ,我们两个路线都可以访问得到 ,所以两个路线交汇 ,不必记录是哪两个路线交汇此处,反正都是同一个级别的分身 所能访问到的地方 ,

    当一条路堵死时候,我们就自动放弃, 寻找同一层次的分身进行下一个级别分身 

    第四步 :三级分身③ (3,1)分身成(4,1),(3,2),标号为④,  同一级别的猴子③ (2,2),也交汇分身到(3,2),都为④

     第五步: 四级分身④ (4,1)分身成⑤(5,1) , 另一同级分身④(3,2) 分身成 ⑤(3,3)

    第六步:五级分身 ⑤(5,1)分身成 ⑥(6,1) ,⑥(5,2) , 另一五级分身⑤ (3,3)分身成 ⑥(3,4)

     第七步 : 六级分身 ⑥(6,1) 分身成 ⑦(7,1) , 另一同级分身⑥(5,2) 分身成⑦(5,3) , 第三个同级分身 ⑥(3,4) 分身成 ⑦(2,4)

    第八步 : 七级分身 ⑦ (7,1) ,无路可走,放弃   

    另一分身 ⑦(5,3) 分身成八级分身 ⑧(6,3) , 

    最后一个同级分身 ⑦(2,4) 分身成 ⑧(1,4)  , ⑧(2,5)

    第九步:  第八级分身 ⑧(6,3)分身成 (6,4) ,

    ⑧(1,4)分身成 ⑨(1,5) 

    ⑧(2,5)分身交汇到 ⑨(1,5) 和 ⑨(2,6)

    第十步 : 九级分身 ⑨(6,4) 分身成 ⑩(6,5) 

    ⑨(1,5) 分身成 ⑩(1,6) 

    ⑨(2,6) 分身交汇到 ⑩(1,6)

    第十一步 : 十级分身 ⑩(6,5) 分身成 ⑪(5,5)  和 ⑪(7,5)

    ⑩(1,6) 遇到无解路线 ,放弃

    第十二步 : 十一级分身 ⑪(5,5) 分身成 ⑫(4,5) 和 ⑫(5,6)

    ⑪(7,5) 分身成⑫(8,5)

    第十三步: 十二级分身 ⑫(8,5) 分身成 ⑬(8,4) 和 ⑬(8,6) 

    ⑫(4,5) 分身成 ⑬(4,6) 

    ⑫(5,6) 分身交汇到 ⑬(4,6)

    第十四步 : 十三级分身 ⑬(4,6) 分身成 ⑭(4,7)

    ⑬(8,6) 分身成 ⑭(8,7)

     第十五步 : 十四级分身 ⑭(8,7) 分身成⑮(8,8) 

    已经达到终点 ,触发奖励 ,达到最优路线 

    我们此时已经到达最优路线 ,线路最短 ,用时最短, 

    能直接宣布胜利吗? 恐怕为时过早 

    我们发现一个问题 ,⑭(4,7) 和 ⑭(5,8) ,如果我们先进行这两个路线的遍历

    ⑭(4,7)分解成 ⑮(3,7)和 ⑮(4,8)

    ⑭(5,8)分解成 ⑮(6,8),交汇⑮(4,8)

    最后才判断 十四级分身 ⑭(8,7) 分身成⑮(8,8) 达到终点 ,

    所以,我们在哪一级分身到达终点 ,需要把那一级的分身都分完 ,再宣布结果也不迟 (如果我们会发现那一级有两条最优路线呢?发现惊喜!)

    那我们如何区分哪条路线是我们要的呢?

    我们就需要从终点进行回溯了, 按照分身级别 

    ⑮(8,8)-->⑭(8,7)-->⑬(8,6)-->⑫(8,5)-->⑪(7,5)-->⑩(6,5)-->⑨(6,4)->⑧(6,3)-->⑦(5,3)------

    ----->⑥(5,2)-->⑤(5,1)-->④(4,1)-->③(3,1)-->②(2,1)-->①(1,1)

    我们可以对路线上进行标记 ,然后我们把其输出即可 ,或者我们在回溯的时候 ,就把路线记下来 ,然后进行对应逆置即可. 

    拓展 :当我们遇到两条最优路线时候 ,可以启用相关的存储,将其存储即可

    我们的人脑模拟已经完成 ,接下来就交给机器了

    下面让我们把思路转化为机器的程序:

    我们回顾我们的过程 , 我们是在迷宫上进行探索的,首先把迷宫表示出来

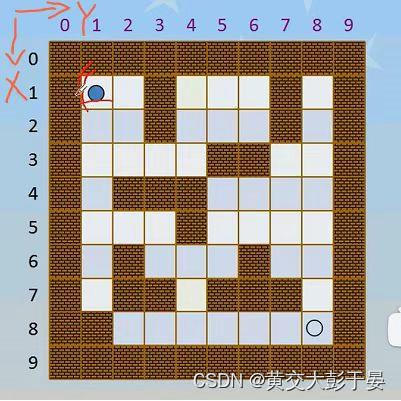
    我们要存储数组 ,就要知道数组的特性 , 涉及到二维数组 ,我们第一个字符代表一行 ,第二个字符代表一行的第几列 ,我们设 x  为行数  ,y 为列数(具体问题具体分析)

    然后 ,我们从(1,1)出发 , 同时前往此节点能够通行的所有节点 ,并前进一步 ,直到成功 ,

    接着进行回溯 ,这时候我们会发现, 如何找到上一个节点,这是个问题 , 我们人脑可以知道 ,逆序的数字 ,就是我们的路线 ,那机器是不知道的 ,所以我们最好在每个节点留下一点线索 ,以方便我们后续的回溯查找 , 

    定义方块结构体

    1. typedef struct
    2. {
    3.     int x,y;//方块的位置
    4.     int pre; //方块在本路径上,上一个方块在队列中的下标
    5. }Box;    //方块类型

    我们接着模拟探索过程 ,我们既然从①开始探索 ,我们其实没有三头六臂 ,孙悟空拔猴毛的时候,也要看一看四周哪些是通路才变分身的

    所以我们定义一个节点的方向 ,以及对应方向所能进行的移动操作

    当我们初始在(1,1)时候 ,方向先设置为 -1 ,然后通过累加, 进行各个方向的模拟通行, 然后如果那个方向是 0 ,则代表通路 ,我们就可以进行对应的分身 ,此分身要表明 自己的坐标 ,从哪一个分身来的 ,以便于后续回溯

    我们先遍历到右方向 , 然后分身 ②(1,2) ,  下方向,分身②(2,1)

    此时我们又遇到一个难题 , 如何进行存储 分身呢?

            我们先看一下此次信息插入和信息检索的特点 , 然后进行对应的数据结构存储

    我们从初始地开始 ,①(1,1) 通过遍历到有通路的点②(1,2) , ② (2,1)

    接着进行分身 ,我们就进行分身存储 ,然后 再接着遍历存储的 二级分身 ,

    二级分身的所有通路遍历完了 ,再将通路存储 

    我们其实是在一端进行探索 ,一端进行存储后续节点 

    这很符合队列的操作

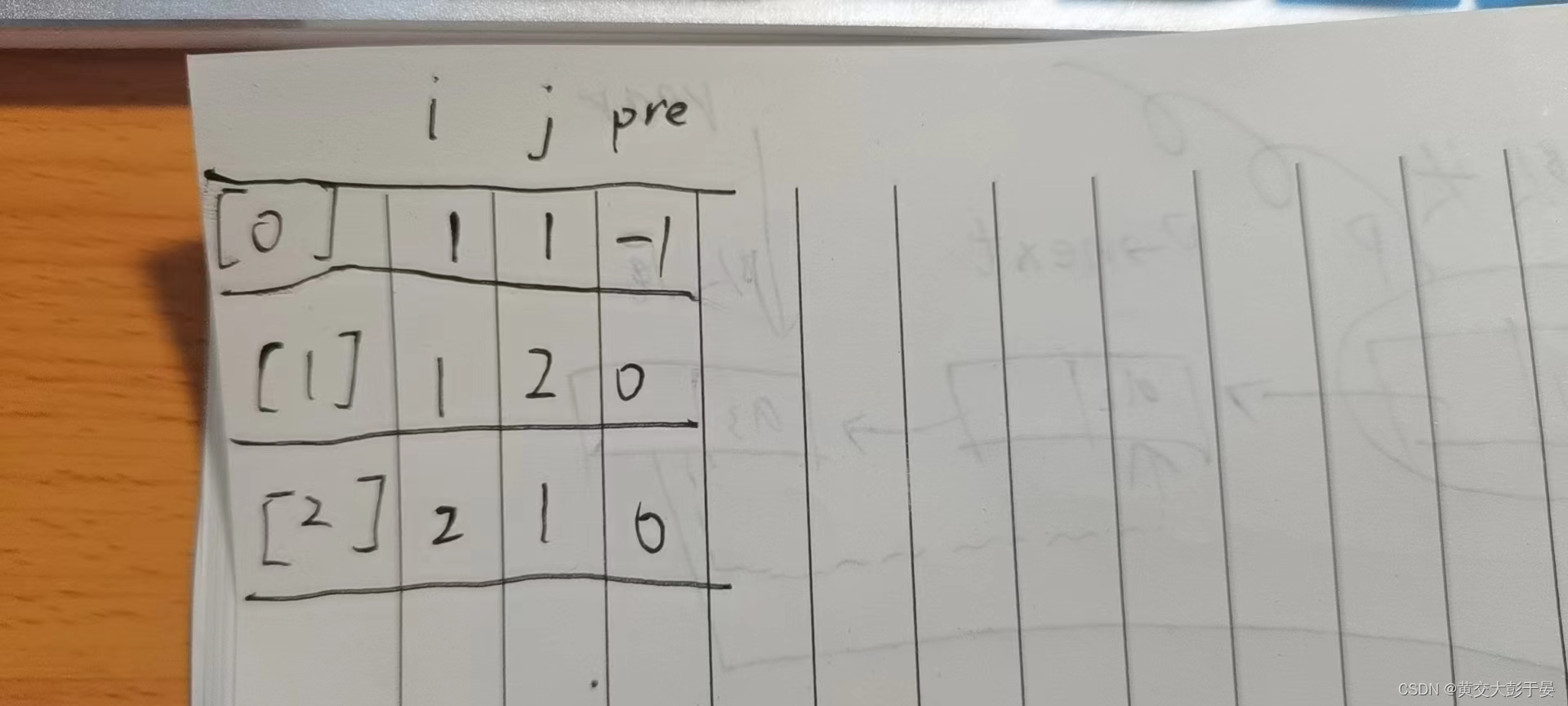
    我们在队首节点进行探索 ,探索到通路之后 ,就可以把通路节点加入到队尾 , 我们因为先来后到的原因 ,我们总是能先把同一级别的分身探索完, 才能探索后面的节点 , 这也保证了 ,我们在平等的探索同一级别的分身 

    但世间哪有绝对的平等 ,同一级别的分身 , 我们在探索一个分身时候 , 另外的分身处于空闲状态 ,这就造成了 上面的交汇的可能 ,其中一个分身把四周都标记分身完了 ,另一个同级分身 ,进行分身的时候 ,看到已经被同级的分身占领 ,只能进行入流 ,或者放弃通路 

    例如, 上面的(3,2) 节点 , 我们可以由(3,1) 或 (2,2) 分身得到 ,但是如果那样的话 ,就需要我们对每一个级别的分身占领的节点 ,进行特殊的标记 ,然后这也会造成回溯的问题 ,这可能需要后续我们使用树形结构来解决了 , 

    由于作者能力有限 ,对于这种同一级别的分身交汇现象 ,由于 队列的局限性 ,我们虽然保证了同一级别的分身 ,优先进行探索,并且在队尾加入后继节点 ,但是 我们在同一级分身,在探索到理论上都可以通过的节点的时候 ,由于同一级别的节点还是有先后顺序 ,这就造成了理论上同一节点都可以占领的节点 ,被其中一个节点占用了 ,另一个同级节点在探索的时候 , 只能选择放弃 ,这也就造成了 ,我们只能选择出一条最优路线 , 而可能的多条最优路线 ,就 因为交汇而不能通过了

    拓展联想:

    如果再在每一个分身层级加一个标记的话 ,如果探索到同类标记就可以进行标记探索 , 而进行回溯的时候 ,如果遇到多个可行路线的话 ,我们可以进行分叉存储 ,这可能使用到后续的树形结构 ,我们现在只能利用队列 ,来求出一条最优路线

    利用队列存储节点 , 队首遍历通路 ,队尾插入分身节点 ,求最优路线的可行性

     我们派大量人力 , 进行分头查找的时候 , 当探索到一条最优路线的时候 , 我们就会停止其他探索 ,

    说明我们是在一个共同的数据路线上进行的探索 , 探索过的节点 ,我们不会再次踏足 ,这也说明了此算法的有穷性 .

    虽然

    我们在探索的时候 , 在同一级别的分身 ,都可以通过一个节点 ,但是被另一个同一级别的节点抢占标记了,回溯的时候 ,也只会回溯那个节点 ,而不会回溯被抢占的节点 , 这也就造成了,无法探索出多条最优路线 ,

    但是

    这不影响我们探索出最优路线,到达终点

    有一句话,叫做"黄河之水天上来 ,奔流到海不复回" ,我们虽然没有对交汇的点进行标记,但是同一级别的分身进行了标记, 当发生交汇的时候 ,只有一种可能 ,就是同一级别的分身,处在对角线 ,而两者都是最优路线 ,因为我们路线长度都一样 ,我们因为队列先后顺序的限制和存储结构的限制 ,不能对两者都进行标记 ,所以也就印证了之前的分析 ,我们利用队列最多只能探索出一条最优路线 .

    但是此队列一定也是最优路线 

    如果 ③(3,1)  抢先对④(3,2) 进行标记 ,说 ④(3,2)来自(3,1) ,那到③(2,2) 对④(3,2)进行探索的时候 ,发现已经被占领了 ,由于队列的局限性 ,我们不能回溯多个路线 ,所以,我们就放弃③(2,2)

    对④(3,2)的交汇标记 , 所以我们就只能探索出一条最优路线了

    我们接下来就对队列存储结构进行定义

    队列存储,我们选用较为简单的数组存储 ,然后用队头和队尾指针指向,

    1. typedef struct
    2. {
    3. 	Box data[MaxSize];
    4. 	int front,rear;
    5. }QuType;

    定义了存储分身的结构, 我们下面就开始队头探索通路

    我们从队头开始模拟

    第一步: 我们在(1,1)出发 ,没有上一个节点pre ,就暂且置为-1

     第二步 : 我们探索队列队首的[0]处节点的通路 ,需要从四个方向,全部探索完 ,然后把通路节点入队

     第三步 : 接着探索队头[2]处通路 ,然后把通路节点入队 ,并且我们入队的坐标信息包括坐标位置和从哪个节点过来的 (为了后续回溯方便,我们在数组队列里面存储上一个节点的信息是,上一个节点的数组坐标序号)

     第 ....步: 我们逐个探索队头的节点 ,如果有通路 ,就把通路节点入队 ,无通路则探索下一个 ,当我们入队的节点到达终点时 ,我们即可跳出遍历

    然后 ,我们就需要把路线输出了 

    我们使用数组存储路线元素 ,一个方便之处就是 ,我们虽然逻辑上出队了元素 ,但是我们的数组里面的节点路线并没有删除 ,只要数组不是循环数组 ,我们就可以根据终点的队尾节点的信息 ,进行回溯 ,通过数组位序 ,就可以找到最优路线上一个节点的信息 ,通过上一个节点的信息又可以探索上上个节点的数组位序 ,从而把相应的坐标都做标记, 通过遍历 ,即可输出最优路线.

    下面把我们的逻辑进行程序化

    探索从(1,1) 到(X,Y)的路径
    (1)首先将(1,1)入队
    (2)在队列qu不为空时循环:
    出队一次(由于不是环形队列 该出队元素仍在队列中),称该出兑的方块为当前方块,
    front为该方块在qu中的下标.
        ①如果当前方块是出口 ,则输出路径并结束
        ②否则按顺时针方向找出当前方块的四个方位中可走的相邻方块(对应的mg数组值为0),
        将这些可走的相邻方块均插入到队列qu中,其pre设置为本搜索路径中上一方块在qu中的下标
        值,也就是当前方块的front值,并将相邻方块对应的mg数组值置为-1 ,以避免回过来重复搜索
    (3)若队列为空仍未找到出口,即不存在路径

    代码实操:

    注意:我们设置了出口,一个是,比较队头元素,如果和目的坐标重合时候,我们就可以输出路径,

    但是大部分时间,我们都是通过队尾元素优先访问到目的地了,我们此时就应该停止探索了,直接调用

     输出路径的函数了,注意传入的参数,是找到目的地后,队列数组的坐标

    1. //头文件
    2. #include 
    3. //定义运算规模
    4. #define MaxSize 100
    5. //定义迷宫规模
    6. #define M 8
    7. #define N 8
    8. //int mgpath(int xi,int yi,int xe,int ye);
    9. //void print(QuType qu,int front);
    10. //用数组来描述迷宫
    11. int mg[M+2][N+2]=
    12. {
    13. 	{1,1,1,1,1,1,1,1,1,1},
    14. 	{1,0,0,1,0,0,0,1,0,1},
    15. 	{1,0,0,1,0,0,0,1,0,1},
    16. 	{1,0,0,0,0,1,1,0,0,1},
    17. 	{1,0,1,1,1,0,0,0,0,1},
    18. 	{1,0,0,0,1,0,0,0,0,1},
    19. 	{1,0,1,0,0,0,1,0,0,1},
    20. 	{1,0,1,1,0,1,1,1,0,1},
    21. 	{1,1,0,0,0,0,0,0,0,1},
    22. 	{1,1,1,1,1,1,1,1,1,1}
    23. };
    24. //定义方块的信息,包括坐标和回溯需要的信息
    25. typedef struct
    26. {
    27. 	int i,j;	//方块在地图的位置
    28. 	int	pre;	//本路径中上一个方块在队列的下标
    29. }Box;
    30. //定义队列的数据结构(包括队首和队尾指针,存储数据节点的数组)
    31. typedef struct
    32. {
    33. 	Box data[MaxSize];
    34. 	int front,rear;	 //队头指针和队尾指针
    35. }QuType;			 //定义顺序队类型
    36.  
    37. //当找到最优路线,制作输出路径的函数
    38. //从队列qu中输出路径, 当front探索到终点时候
    39. //传入路径最后的数组位序front
    40. void print(QuType qu,int front)	  
    41. {
    42. 	//当然是回溯,然后标记路径,然后输出最优路线坐标
    43. 	int k = front;
    44. 	int j;
    45. 	int ns = 0;
    46. 	printf("\n");
    47.     //反向找到最短路径,将该路径上的方块的pre成员设置成-1	
    48. 	do
    49. 	{
    50. 		j=k;
    51. 		k=qu.data[k].pre;
    52. 		qu.data[j].pre = -1;
    53. 	}
    54. 	while(k!=0);	//初始地就是数组位序为0处
    55. 	printf("迷宫路径如下:\n");
    56. 	k=0;
    57. 	//正向搜索pre为-1的方块,即构成正向的路径
    58. 	while(k<=front)
    59. 	{
    60. 		//如果数组元素pre为-1,则将其元素的坐标输出
    61. 		if(qu.data[k].pre == -1)
    62. 		{
    63. 			//这里可以设置换行输出
    64. 			ns++;
    65. 			printf("\t(%d,%d)",qu.data[k].i,qu.data[k].j);
    66. 			if(ns%5==0)
    67. 			{
    68. 				printf("\n");	//没输出5个方块后换行
    69. 			}			
    70. 		}
    71. 		k++;
    72. 	}
    73. 	printf("\n");
    74. }
    75.  
    76. //我们首先传入出发地和终点的坐标
    77. //搜索路径为(xi,yi)-->(xe,ye)
    78. int mgpath(int xi,int yi,int xe,int ye)
    79. {
    80. 	//定义存储坐标的变量
    81. 	int i,j;
    82. 	//然后我们要存储节点数据,所以先把队列定义
    83. 	QuType qu;
    84. 	//初始的时候,队头和队首指针指向-1,方便后续累加使用
    85. 	qu.front = qu.rear = -1;
    86. 	//现在让猴哥落地到出发地,队尾指针加一
    87. 	qu.rear++;
    88. 	//对应队列元素的节点坐标
    89. 	qu.data[qu.rear].i = xi;
    90. 	qu.data[qu.rear].j = yi;//(xi,yi)进队
    91. 	//因为此时是初始节点入队,其未有上个路线节点,我们置为-1
    92. 	qu.data[qu.rear].pre = -1;
    93. 	//相应地图坐标已经占用
    94. 	//将其赋值-1,以避免回过来重复搜索
    95. 	mg[xi][yi] = -1;	
    96. 	//接下来开始探索队首节点的节点,然后将其通路节点入队
    97. 	//队列不为空且未找到路径时循环
    98. 	int find =0; //未找到路径
    99. 	//我们入队元素,就表明我们已经触发寻找机制,直到队首和队尾重合
    100. 	//即使把所有节点都探索完为止
    101. 	int di; //定义方向
    102. //	int k_1=0;  //测试次数
    103. 	while(qu.front!=qu.rear && !find)
    104. 	{
    105. 	 //出队,由于不是环形队列，该出队元素仍在队列中
    106. 		qu.front++;
    107. 		//对比队列对头的元素,是否为出口坐标
    108. 		i = qu.data[qu.front].i;
    109. 		j = qu.data[qu.front].j;
    110. 		if(i == xe && j==ye) 
    111. 		{
    112. //			printf("你是傻逼\n");
    113. //			printf("k的值是:%d\n",k_1);
    114. 			//如果找到重点,则标记find,跳出循环
    115. 			find = 1;
    116. 			//调用print函数输出路径
    117. 			print(qu,qu.front);
    118. 			return (1);
    119. 		}
    120. 		//如果没有找到,我们则
    121. 		//循环扫描每个方位,把每个可走的方块插入队列中
    122. 		for(di = 0;di<4;di++)
    123. 		{
    124. 			switch(di)
    125. 			{
    126.             case 0:
    127.                 i=qu.data[qu.front].i-1;
    128.                 j=qu.data[qu.front].j;
    129.                 break;
    130.             case 1:
    131.                 i=qu.data[qu.front].i;
    132.                 j=qu.data[qu.front].j+1;
    133.                 break;
    134.             case 2:
    135.                 i=qu.data[qu.front].i+1;
    136.                 j=qu.data[qu.front].j;
    137.                 break;
    138.             case 3:
    139.                 i=qu.data[qu.front].i, j=qu.data[qu.front].j-1;
    140.                 break;
    141. 			}
    142. 			//如果对应的方向可走,则进行入队操作
    143. 			if(mg[i][j]==0)
    144. 			{
    145. 				//队指针加一
    146. 				qu.rear++;
    147. 				//队数组元素坐标赋值
    148. 				qu.data[qu.rear].i=i;
    149. 				qu.data[qu.rear].j=j;
    150. 				
    151. 				//队元素回溯数据,指向路径中上一个方块的下标
    152. 				//此时到此节点的数据,就是队首指针指向的元素
    153. 				qu.data[qu.rear].pre = qu.front;
    154. 				//对应地图坐标被占用,记作-1
    155. 				//将其赋值-1,以避免回过来重复搜索
    156. 				mg[i][j]=-1;
    157.  
    158. //				k_1++;
    159. //				printf("k运行次数%d\n",k_1);
    160. 				if(i == xe && j==ye) 
    161. 				{
    162. //					printf("你是傻逼!");
    163. 					//如果找到重点,则标记find,跳出循环
    164. 					find = 1;
    165. //					printf("qu.rear值是%d\n",qu.rear);
    166. //					调用print函数输出路径
    167. 					print(qu,qu.rear);
    168. 					return (1);
    169. 				}
    170. 			}
    171. 		}
    172. 	}
    173. 	//当访问了,所有能到达的所有节点,仍未找到则跳出,返回0	
    174. 	return (0);
    175. }
    176.  
    177. //主函数传入入口和重点
    178. int main()
    179. {
    180. 	int h;
    181. 	h = mgpath(1,1,M,N);
    182. 	if(h==1)
    183. 	{
    184. 		printf("恭喜你,找到出口!\n");
    185. 	}else if(h==0)
    186. 	{
    187. 		printf("很抱歉,未能找到出口!\n");		
    188. 	}
    189. 	return 0;
    190. }

  • 相关阅读:
    Etcd教程 — 第七章 Etcd之事务API
    Sublime Text Mac/Win中文版：代码编辑器的卓越典范
    【EasyExcel】第二篇：导出excel文件，导出多个sheet工作空间
    亚商投资顾问 早餐FM/12022023年开展第五次全国经济普查
    优优嗨聚集团：餐饮发展与房地产的关联：一种强效应的探索
    Linux：理解进程的多种状态
    继承【C++】
    7-171 找出最小值
    在线OJ项目(1)------实现代码编译运行功能
    C—数据的储存（下）
  • 原文地址：https://blog.csdn.net/qq_57484399/article/details/127392294