【笔试刷题训练】day_05

选择题

显然，每一次进入x都从1++到2
但是走到while循环判断的时候又–变成1
所以x永远是1 死循环 选D

strlen遇到\0结束，所以strlen(dog)为4
sizeof()计算\0，数组最后还有一个\0，所以sizeof(dog)为10

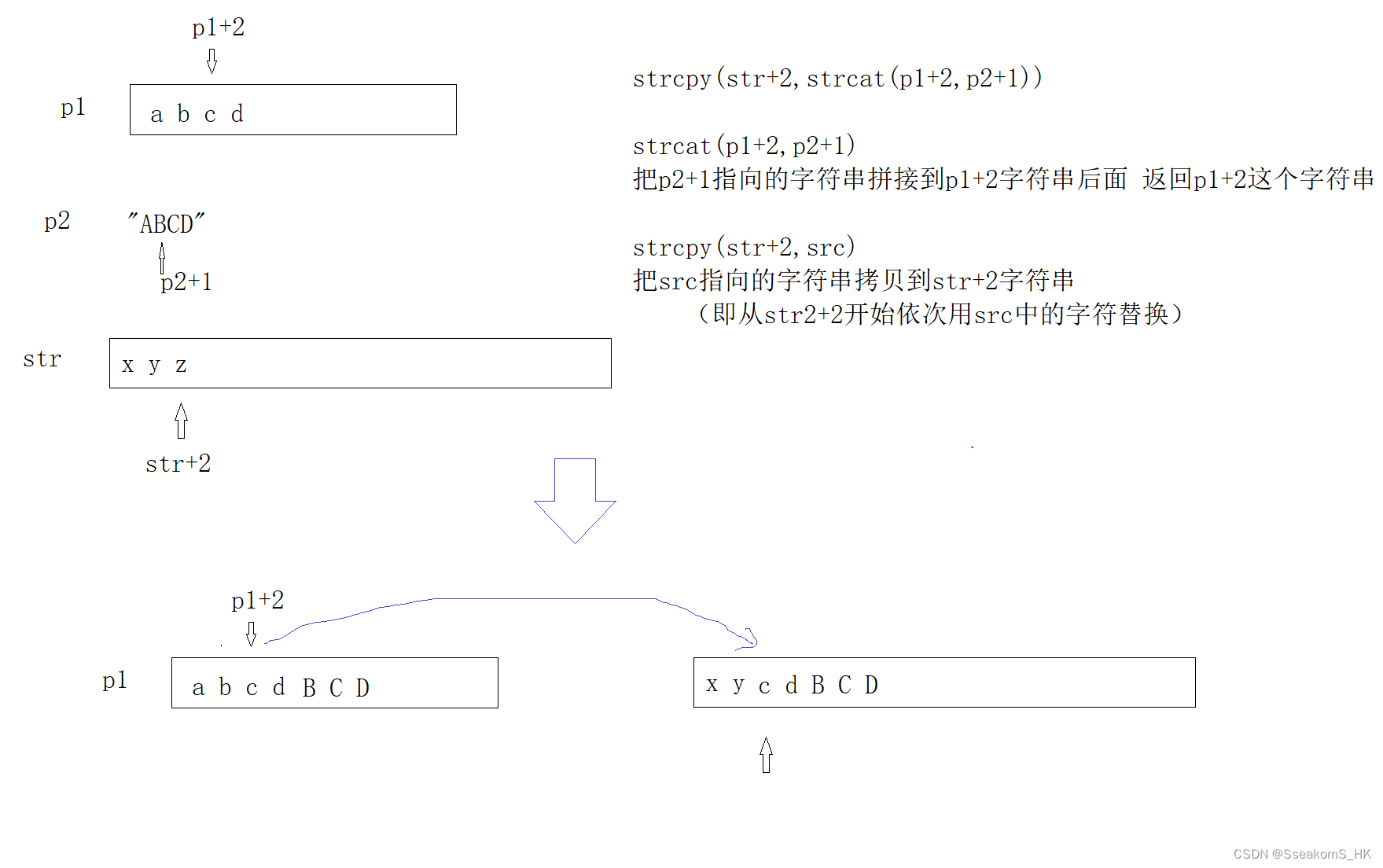
所以最终答案为xycdBCD,选D

在对齐数位4的情况下：

one:
	double:0 1 2 3 4 5 6 7
	char:8
	空 9 10 11
	int:12 13 14 15
共16字节，已对齐
two:
	char:0
	空 1 2 3
	double: 4 5 6 7 8 9 10 11 
	int:12 13 14 15 
共16字节，已对齐
1
2
3
4
5
6
7
8
9
10
11
12

在对齐数位8的情况下：
不同点：double类型需要偏移量为8的情况下才可以存放，因为要取double类型和默认对齐数的较小值，都是8，所以为8

one:
	double:0 1 2 3 4 5 6 7
	char:8
	空 9 10 11
	int:12 13 14 15
共16字节，已对齐
two:
	char:0
	空 1 2 3 4 5 6 7
	double:8 9 10 11 12 13 14 15
	int:16 17 18 19
共20字节，不是8的倍数
对齐后：24字节
1
2
3
4
5
6
7
8
9
10
11
12
13

所以：one在对齐数为4和8的时候都是16字节
two在对齐数为4的时候为16，对齐数为8的时候为24

类比二维数组
如int a[2][3]
那么a[1][2]==*(*(a+1)+2)
所以答案选B

编程题

1. 统计回文

👉 题目链接

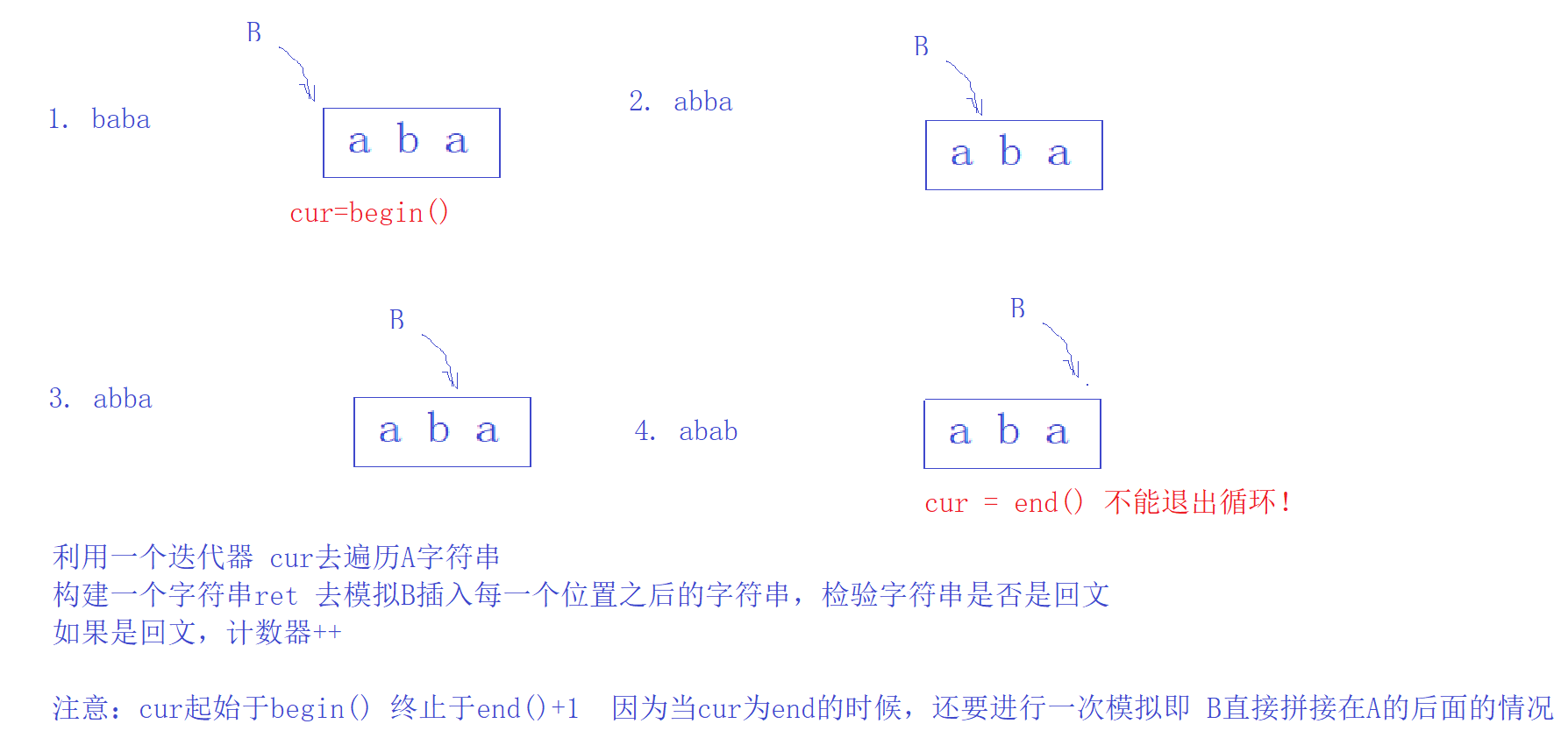
#include
using namespace std;
#include
// abba
bool isPail(const string& str)
{
    auto begin = str.begin();
    auto end = str.end()-1;
    while(begin < end)
    {
        if(*begin != *end)
        {
            return false;
        }
        ++begin;
        --end;
    }
    return true;
    
}
int main()
{
    string A,B;
    cin>> A >> B;

    int count = 0;
    //遍历字符串A，对每一个位置插入字符串B都进行回文检验
    auto cur = A.begin();
    //这里 cur走到end()+1才退出
    while(cur != A.end()+1)
    {
        //   begin    end
        const string ret = string(A.begin(),cur) + B + string(cur,A.end());//构造
        if(isPail(ret))
        {
            ++count;
        }
        ++cur;
    }
    cout << count << endl;
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

2. 连续最大和

👉 题目链接

贪心

定义一个sum记录前面累加的和，Max为最大和

当前面累计和为负数的时候，就从当前位置重新加，重新计算和

因为前面累计的和已经为负数了，加上当前位置的元素之后还不如不加之前的和，会做出负贡献，所以从当前位置开始计算新的和

如果是正数，那么sum直接加上当前位置的元素的值，因为sum可以有正贡献

每加一个数，都比较sum和最大和Max，如果大于最大和，最大和更新。 最后得到的就是最大连续子数组和

#include
#include
#include
#include
using namespace std;
int main()
{
    //贪心
    int n;
    cin >> n ;
    vector<int> v;
    v.resize(n);
    for(size_t i = 0;i < n;++i)
    {
        cin >> v[i];
    }
    long long Max = v[0];
    long long sum = v[0];
    for(size_t i = 1;i < n ;++i)
    {
        if(sum < 0)
        {
            sum = v[i];
        }
        else
        {
            sum += v[i];
        }
        Max = max(sum,Max);
    }
    cout << Max << endl;
     return 0;   
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

动规

#include
#include
#include
using namespace std;
int main()
{
	vector<int> v;
	int n;
	cin >> n;
	v.resize(n);
	for (size_t i = 0; i < n; ++i)
	{
		cin >> v[i];
	}

	int* dp = new int[n];
	dp[0] = v[0];//初始状态
	int Max = v[0];
	for (size_t i = 1; i < n; ++i)
	{
		//状态转移
		dp[i] = max(dp[i - 1] + v[i], v[i]);
		Max = max(dp[i],Max);
	}

	//输出最大值
	cout << Max << endl;
	
	return 0;


}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32