回归-线性回归算法（房价预测项目）

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。

简介

---

线性回归（Linear Regression）是回归任务中最常见的算法，利用回归方程对自变量和因变量进行建模，且因变量和自变量之间是线性关系而得名，从而可以根据已知数据预测未来数据，如房价预测、PM2.5预测等。

其中，只有一个自变量则称为一元线性回归，包含多个自变量则成为多元线性回归。

如下图，根据已知数据点（蓝色），建模得到红色的回归方程，表示自变量和因变量关系，从而可以输入新的自变量，得到预测值（因变量）。

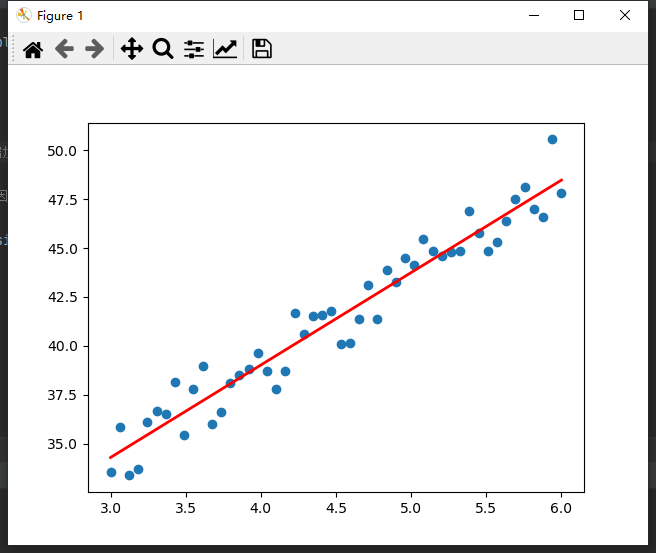
预测函数定义为：
$$h(w)=w_1{x}_1+w_2{x}_2+\cdot \cdot \cdot +w_d{x}_d+b$$

向量形式为：
$$h(w)={\mathbf{w}}^{\mathbf{T}}\mathbf{x}$$
其中 w T = ( b w 1 ⋅ ⋅ ⋅ w d ) , x = ( 1 x 1 ⋅ ⋅ ⋅ x d ) \bold{w^T}=(bw1···wd)

,\bold{x}=(1x1···xd) wT=⎝⎜⎜⎛​bw1​⋅⋅⋅wd​​⎠⎟⎟⎞​​,x=⎝⎜⎜⎛​1x1​⋅⋅⋅xd​​⎠⎟⎟⎞​​

也就是说我们需要确定$\mathbf{w}$和$b$的值，来构建预测函数。

假设随机初始化$\mathbf{w}$和$b$后，我们得到一个预测函数$h_w$，我们的目标就是希望$h_w$尽可能贴近目标函数。那又要如何评价当前构建出来的模型怎么样，评价两个模型的优劣，并如何向目标函数不断靠近呢？

即使用损失函数和优化算法。

损失函数

---

损失函数就是定义当前函数和目标函数之间的差异，并且我们期望这个差异（损失）越小越好。

使用误差平方和SSE来表示损失，即预测值和真实值差的平方求和，该方法也称为最小二乘法，二乘即平方的意思，求最小的损失。

总损失定义为：
$$J(w)=\frac{1}{2}\sum _{i=1}^m(h_w(x_i)-y_i{)}^2=\frac{1}{2}(\mathbf{x}\mathbf{w}-\mathbf{y}{)}^2$$
其中$h_w(x_i)$表示训练样本$i$的预测值，$y_i$是训练样本$i$的真实值。

也就是使下图中黄色长度之和最小。

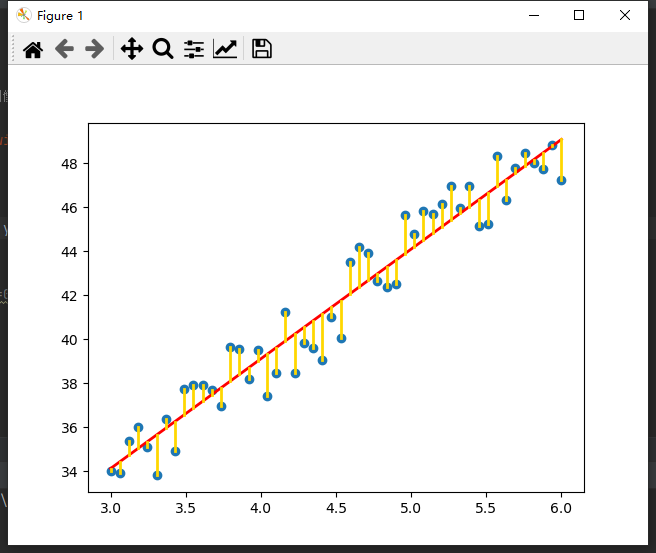
优化算法

正规方程

---

利用高中知识，求一个函数的最小值，我们可以求导，在导数为0处取得最小值。
这也是为什么损失函数乘以$\frac{1}{2}$，为了求导后可以约掉。

对$\mathbf{w}$求导：
$$\begin{gathered} (\frac{1}{2}(\mathbf{x}\mathbf{w}-\mathbf{y}{)}^2{)}^{{}^{\prime }}=0 \\ (\mathbf{x}\mathbf{w}-\mathbf{y})\mathbf{x}=0 \\ (\mathbf{x}\mathbf{w}-\mathbf{y})(\mathbf{x}{\mathbf{x}}^T)=0 \\ (\mathbf{x}\mathbf{w}-\mathbf{y})(\mathbf{x}{\mathbf{x}}^T)(\mathbf{x}{\mathbf{x}}^T{)}^{-1}=0 \\ \mathbf{x}\mathbf{w}-\mathbf{y}=0 \\ \mathbf{x}\mathbf{w}=\mathbf{y} \\ {\mathbf{x}}^T\mathbf{x}\mathbf{w}={\mathbf{x}}^T\mathbf{y} \\ ({\mathbf{x}}^T\mathbf{x}{)}^{-1}({\mathbf{x}}^T\mathbf{x})\mathbf{w}=({\mathbf{x}}^T\mathbf{x}{)}^{-1}{\mathbf{x}}^T\mathbf{y} \\ \mathbf{w}=({\mathbf{x}}^T\mathbf{x}{)}^{-1}{\mathbf{x}}^T\mathbf{y} \end{gathered}$$

一顿操作之后，也就是说如果${\mathbf{x}}^T\mathbf{x}$可逆（是正定矩阵），我们就可以直接求得最小损失对应的$\mathbf{w}$。
但是该方法适合样本特征数比较小的情况，不然矩阵太大了运算也很慢，因为复杂度是O(N³)。

使用numpy和scipy提供的矩阵运算，可以得到代码实现：

def Regres(X, Y):
    x = mat(X)  # 创建矩阵
    y = mat(Y).T  # 处理y为一列
    if linalg.det(x.T * x) == 0.0:  # 不可逆
        return 0
    else:
        return (x.T * x).I * (x.T * y)
1
2
3
4
5
6
7

梯度下降

---

如果可逆，通过正规方程可以一步到位求得最优模型的参数$\mathbf{w}$。但如果不可逆，就不能使用该方法了。

使用梯度下降可以求得最小的损失值，其主要思想是求偏导按照梯度上升最快的方向进行求解，取其梯度反方向，即梯度下降。

比如三维特征中，其平面图可以像是山峰和谷底，那我们就是要从山峰出发，从最陡（梯度最大）的方向进行下山，从而到达谷底取最小值，但往往可能陷入其它谷底，只取到了极小值，可以修改步长（学习率）。

梯度下降算法内容较多，可见另一篇：浅谈梯度下降与模拟退火算法。

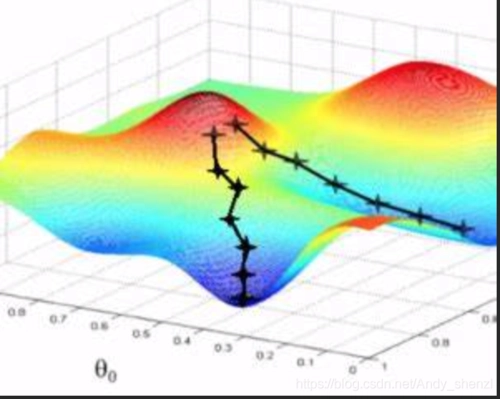
上图摘自网络。

（插播反爬信息 ）博主CSDN地址：https://wzlodq.blog.csdn.net/

项目实战

---

使用波士顿房价数据集，sklearn内置了该数据集，也是Kaggle中的一个入门练习。共506条数据，13个特征。

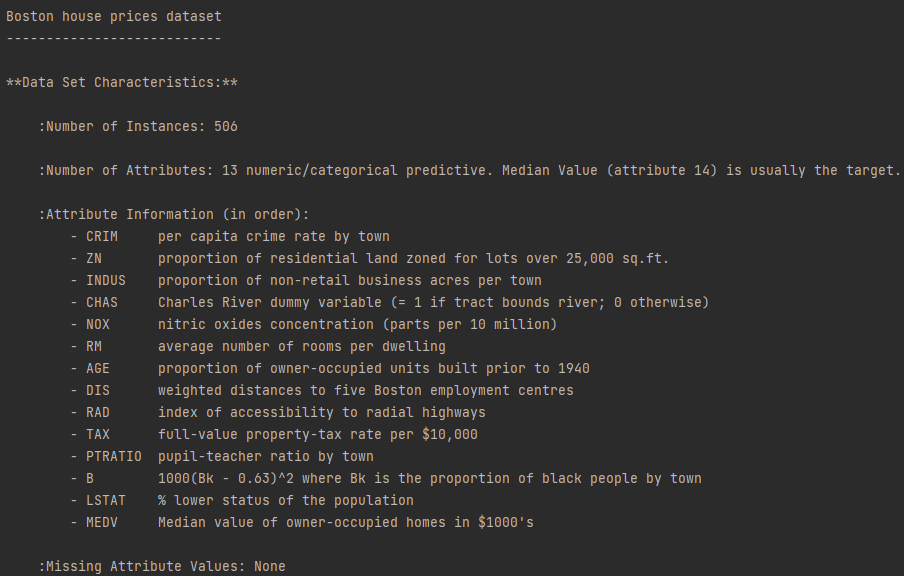
sklearn库提供了两个线性模型API：

1. LinearRegression()正规方程

fit_intercept：默认True，是否计算偏置
normalize：默认False，是否中心化
copy_X：默认True，否则X会被改写
n_jobs：默认为1，表示使用CPU的个数。当-1时，代表使用全部CPU

LinearRegression.coef_：回归系数
LinearRegression.intercept_：偏置

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 正规方程
# 获取数据
boston = load_boston()
# 划分训练集测试集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=20221001)
# 特征工程
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 训练模型
model = LinearRegression()
model.fit(x_train, y_train)
# 测试模型
y_pre = model.predict(x_test)
print("预测值：", y_pre)
# 评估模型
print("准确率：", model.score(x_test, y_test))
print("均方误差：", mean_squared_error(y_test, y_pre))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

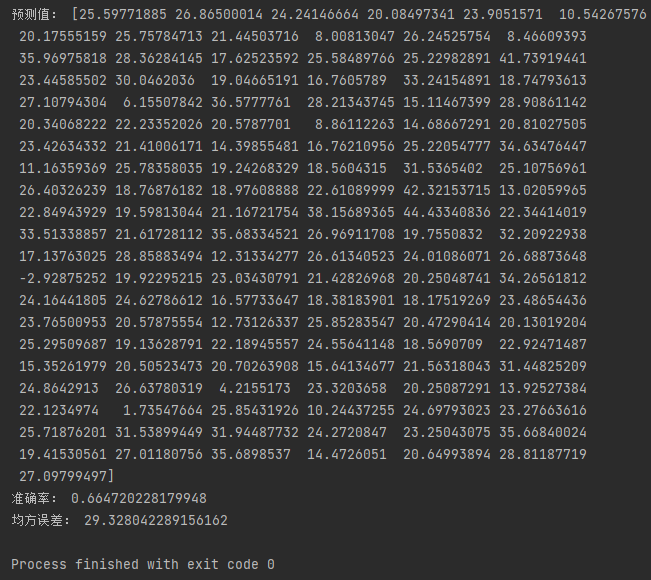
2. SGDRegressor()随机梯度下降

loss：损失函数，squared_loss最小二乘法
fit_intercept：是否计算偏置
learning_rate：学习率，“constant”：eta = eta0；“optimal”：eta = 1.0 / (alpha * (t + t0))；“invscaling”：eta = eta0 / pow(t, power_t)

SGDRegressor.coef_：回归系数
SGDRegressor.intercept_：偏置

from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 随机梯度下降
# 获取数据
boston = load_boston()
# 划分训练集测试集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=20221001)
# 特征工程
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.fit_transform(x_test)
# 训练模型
model = SGDRegressor()
model.fit(x_train, y_train)
# 测试模型
y_pre = model.predict(x_test)
print("预测值：", y_pre)
# 评估模型
print("准确率：", model.score(x_test, y_test))
print("均方误差：", mean_squared_error(y_test, y_pre))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

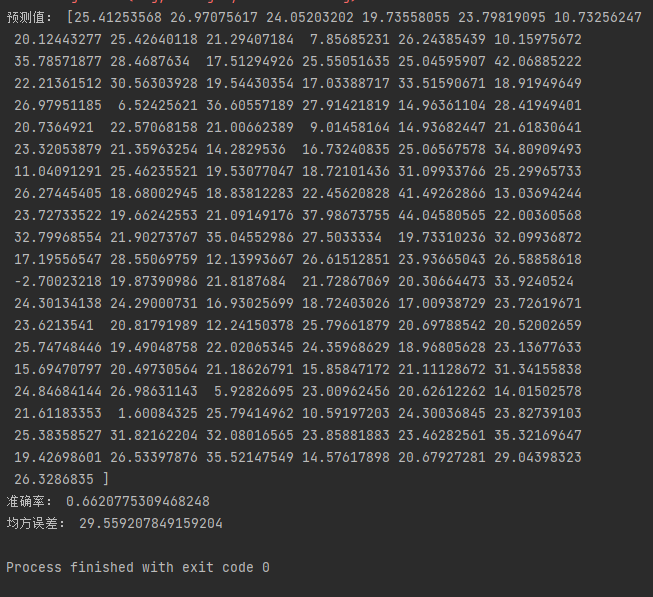
使用深度学习-Pytorch库求解，可查看另一篇博客Pytorch-张量tensor详解（线性回归实战）

原创不易，请勿转载（本不富裕的访问量雪上加霜 ）
博主首页：https://wzlodq.blog.csdn.net/
来都来了，不评论两句吗👀
如果文章对你有帮助，记得一键三连❤