树状数组基本操作

一维树状数组

如果我们想实现求前缀和 和 修改某一个数的操作，用普通数组来做时间复杂度分别是 O(n) 和 O(1),但如果用树状数组来做时间复杂度都为log(n),降低了整体时间复杂度。

 

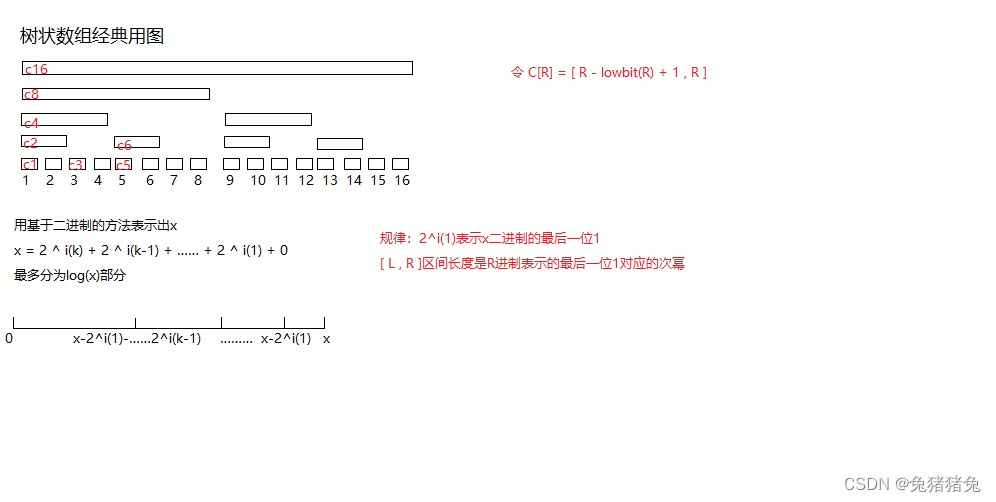
通过上图下方的设计，可以在log(n)时间内求出前缀和。

树状数组有两个核心的操作：

void add(int x, int c)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
 
int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

 第一个操作为单点修改，第二个操作为单点查询

难道树状数组只能支持这两个操作吗？

非也非也，通过一些技巧，树状数组能拓展出很多功能。

1.区间修改与单点查询-----差分

例题：一个简单的整数问题242. 一个简单的整数问题 - AcWing题库

假如需要修改的区间为 [ L , R ] ,则只需要维护一个差分树状数组，在 L 的位置加上需要加的数，在 R+1 的位置减去即可。

2.区间修改与区间求和----二维前缀和、差分

例题：一个简单的整数问题2243. 一个简单的整数问题2 - AcWing题库

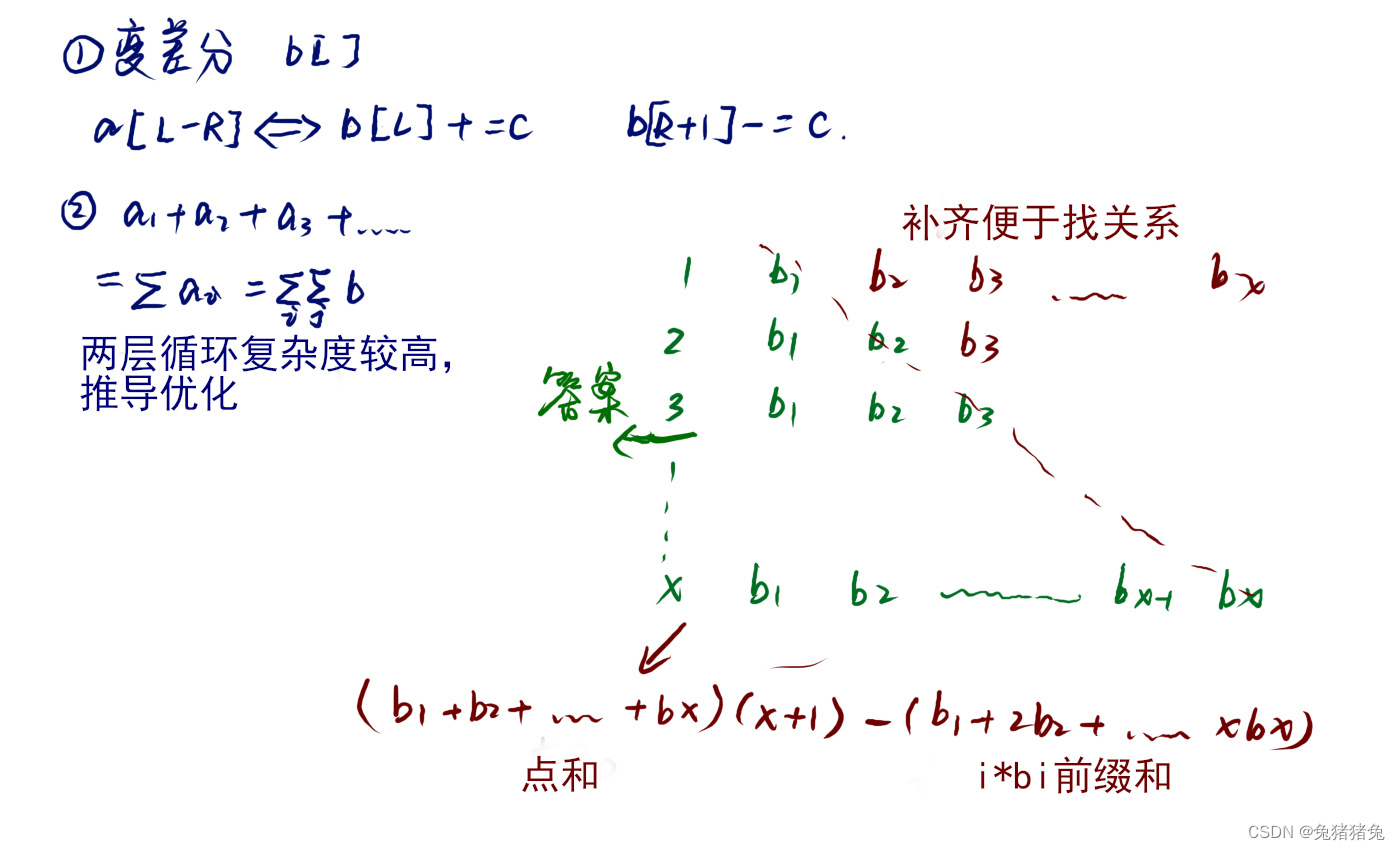
 3.剩余数中第k小的数，删除某一个数----树状数组维护“1”的前缀和+二分

如果一个数存在则记为1，原问题1转化为找出一个最小的数使得 sum [ x ] = k ,二分即可。

删除一个数则赋为0。

例题：谜一样的牛244. 谜一样的牛 - AcWing题库

二维树状数组

因为我也没学过，所以参考了其他博客。

感觉 二维树状数组总结及模板_Lv1_kangdi的博客-CSDN博客_二维树状数组 将操作讲的很透彻，但是没具体说二维树状数组的含义，在数据结构——二维树状数组_星*湖的博客-CSDN博客_二维树状数组 中说，在二维树状数组中，arr[x][y] 记录的是右下角为​(x,y)，高度为 lowbit(x)，宽度为 lowbit(y) 的区间和。