One class learning(SVDD)

常见的分类问题分为二分类和多分类，而多分类可以拆解为多个二分类问题。在二分类问题中，分类器对一个的样本的判断为非正即负，分类结果一定是二者之一。

理想情况下，二分类中的每类样本数据要求巨大且相等。但是在现实世界却往往是相反的，在二分类问题中，正负类样本可能是严重失衡，这种情况也有解决的办法，那就是不平衡性学习。而考虑到极端情况，某一类样本少到几乎没有，但是又及其重要时应该如何分类？这就出现了 one class classification。仅有一类样本用于训练，而其他类别总称为（outlier）信息缺失。

例子：

有一个数据集包含苹果和梨子的样本，每个样本有2个特征：宽度和重量，数据集中的每个样本都可以表示为2维空间的一个点，红色*表示苹果，蓝色的+表示梨，虚线内的样本表示整个训练集。

对于二分类问题来说，图中的黑线正好可以将数据集中的样本分成苹果或者梨，即使新来一个样本，分类的结果也只能苹果或者梨子；

对于one class classification 来说，整个训练集为一类，把苹果+梨作为一个类别，而虚线则是这个类的范围，如果在虚线内则认为是属于苹果+梨类，反之，如图中黑点，则是不属于苹果+梨类，至于到底是属于什么类不清楚，分类器只知道是或者不是属于该类。

当训练集不是二维的时候，图中的虚线也转变成了一个封闭的超球面，把整个训练集包裹，在球面内的则是属于该类，外面则是其他类。

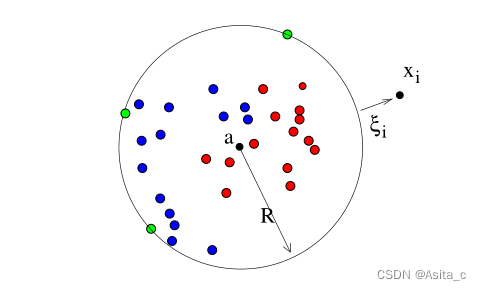
有一个找这个超球面的算法叫做：
支持向量数据描述 support vector data description(SVDD) 是一种单值分类算法，能够实现目标样本和非目标样本的区分，通常应用于异常检测和故障检测等领域。

其原理如下：
对于一组正类训练数据 $\mathbf{x}\in R^{n\times d}$ ，其中 $n$ 是样本个数，$d$ 是特征维度。首先通过非线性变换函数 $\Phi :\mathbf{x}\to \mathbf{F}$ 将数据从原始空间映射到特征空间，然后在特征空间中寻找一个体积最小的超球体，为了构造这样最小的超球体，SVDD需要解决以下优化问题：
min ⁡ ε ( a , R , ξ ) = R 2 + C ∑ i = 1 n ξ i s . t . { ∥ x i − a ∥ 2 ≤ R 2 + ξ i ξ i ≥ 0 ∀ i = 1 , 2 , … , n \min\varepsilon(\mathbf{a},R,\xi)=R^2+C\sum_{i=1}^{n}\xi_i \\ s.t.

\\ minε(a,R,ξ)=R2+Ci=1∑n​ξi​s.t.⎩ ⎨ ⎧​∥xi​−a∥2≤R2+ξi​ξi​≥0∀i=1,2,…,n​
其中，$R$ 是为超球体半径，$\mathbf{a}$ 为球心，$\xi$ 为松弛因子，$C$ 为权衡超球体和误分率的惩罚参数。

该优化问题求解：
1、首先根据拉格朗日乘子法构造拉格朗日函数：
L ( R , a , ξ , α , γ ) = R 2 + C ∑ i = 1 n ξ i − ∑ i = 1 n α i { R 2 + ξ i − ( x i ⋅ x i − 2 a ⋅ x i + a ⋅ a ) } − ∑ i = 1 n γ i ξ i L(R,\mathbf{a},\xi,\alpha,\gamma)=R^2+C\sum_{i=1}^n\xi_i-\sum_{i=1}^n\alpha_i\{R^2+\xi_i-(\mathbf{x}_i\cdot\mathbf{x}_i-2\mathbf{a}\cdot\mathbf{x}_i+\mathbf{a}\cdot\mathbf{a})\}-\sum_{i=1}^n\gamma_i\xi_i L(R,a,ξ,α,γ)=R2+Ci=1∑n​ξi​−i=1∑n​αi​{R2+ξi​−(xi​⋅xi​−2a⋅xi​+a⋅a)}−i=1∑n​γi​ξi​
对于$R、\mathbf{a}$来说$L$必须最小化，而对于$\alpha 、\gamma$来说，$L$ 必须最大化。

分别对每个变量求偏导为0：
$$\frac{\partial L}{\partial R}=2R-2R\sum _{i=1}^n{\alpha }_i=0,即：\sum _{i=1}^n{\alpha }_i=1$$
$$\frac{\partial L}{\partial \mathbf{a}}=2\sum _{i=1}^n{\alpha }_i{\mathbf{x}}_i-2\mathbf{a}=0，即\mathbf{a}=\sum _{i=1}^n{\alpha }_i{\mathbf{x}}_i$$
$$\frac{\partial L}{\partial \xi }=C-{\alpha }_i-{\gamma }_i=0，即0\le {\alpha }_i\le C$$
把结果带入到 $L$ 中得到：
$$\begin{gathered} L={\mathbf{x}}_i\cdot {\mathbf{x}}_i-2\sum _{i=1}^n{\alpha }_i({\mathbf{x}}_j\cdot {\mathbf{x}}_i)-\sum _{i=1,j=1}^n{\alpha }_i{\alpha }_j({\mathbf{x}}_i,{\mathbf{x}}_j) \\ s.t.0\le {\alpha }_i\le C,\sum _{i=1}^n{\alpha }_i=1 \end{gathered}$$

对于在球内的对象 $\mathbf{z}$ 到球心的距离有：
$$\Vert \mathbf{z}-\mathbf{a}{\Vert }^2=(\mathbf{z}\cdot \mathbf{z})-2\sum _i{\alpha }_i(\mathbf{z}\cdot {\mathbf{x}}_i)+\sum _{i,j}{\alpha }_i{\alpha }_j({\mathbf{x}}_i\cdot \mathbf{z})\le R^2$$
若$\mathbf{z}$ 为超球面边界上的点时：
$$R^2=({\mathbf{x}}_k\cdot {\mathbf{x}}_k)-2\sum _i{\alpha }_i({\mathbf{x}}_k\cdot {\mathbf{x}}_i)+\sum _{i,j}{\alpha }_i{\alpha }_j({\mathbf{x}}_i\cdot {\mathbf{x}}_k)$$

因此，对于满足 ${\mathbf{x}}_k\in S{V}^{bnd}$，即处于超平面内，即$0\le {\mathbf{x}}_k\le C$的支持向量集，我们称这种单分类器为支持向量数据描述（SVDD）,记为：
f S V D D ( z ; α , R ) = I ( ∥ z − a ∥ 2 ≤ R 2 ) = I ( ( z ⋅ z − 2 ∑ i α i ( z ⋅ x i ) + ∑ i , j α i α j ( x i ⋅ x j ) ≤ R 2 )

fSVDD(z;α,R)​​=I(∥z−a∥2≤R2)=I((z⋅z−2i∑​αi​(z⋅xi​)+i,j∑​αi​αj​(xi​⋅xj​)≤R2)​

可以得到超球体的球心和半径的计算公式为：
$$\mathbf{a}=\sum _{i=1}^n{\alpha }_i({\mathbf{x}}_i)$$
$$R=\sqrt{(\mathbf{z}\cdot {\mathbf{x}}_i)-2\sum _{i=1}^n{\alpha }_i(\mathbf{z}\cdot {\mathbf{x}}_i)+\sum _{i,j=1}^n{\alpha }_i{\alpha }_j({\mathbf{x}}_i{\mathbf{x}}_j)}$$

---

参考文献：http://homepage.tudelft.nl/n9d04/thesis.pdf