二叉树基础

二叉树中的常用术语：

结点（Node）：包含一个元素和若干指向其子树的分支
结点的度（Degree）：一个结点拥有的子树的个数称为该节点的度
树的度：一棵树的度是指该树中节点的最大度数。
叶子（Leaf）结点：树中度为0的结点称为叶子结点或者终端结点。
分支结点：树中度不为0的结点称为分支结点或非终端结点。一棵树的结点 除叶子结点外，其余的结点都是非终端结点，除根节点外的非终端节点也称为是内部结点。
结点的层次（Level）：结点的层次是从根开始定义，根节点的层次为1，其孩子结点为2。依次类推，任意结点的层次为其双亲的结点层次加1.
树的深度：树中结点的最大层次称为书的深度或高度。

二叉树分类

1、完全二叉树

若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。
一维数组可以作为完全二叉树的存储结构，堆排序使用的数据结构就是完全二叉树。

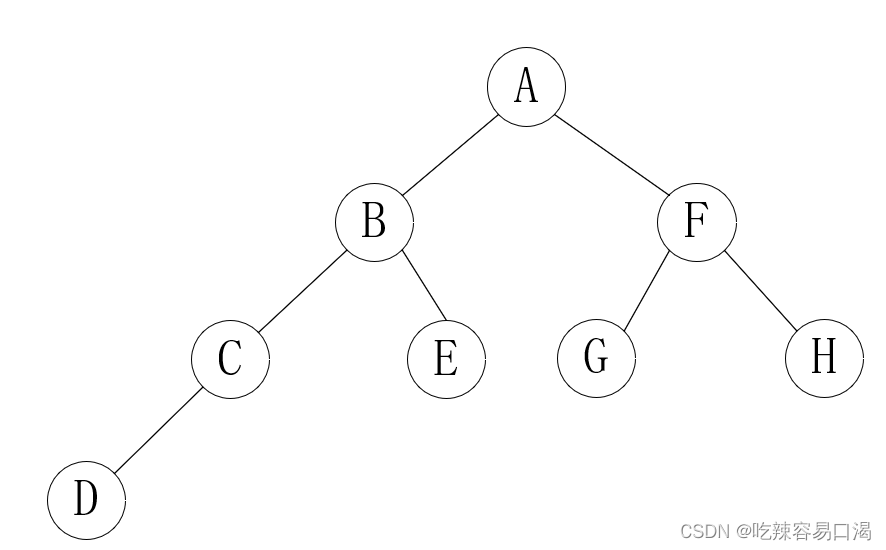
2、满二叉树

国际标准定义：除了叶结点外每一个结点都有左右子结点的二叉树

国内的定义是：除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。很显然，按照这个定义，上面的图示二叉树就不是满二叉树。
注意：满二叉树 一定是完全二叉树，而完全二叉树不一定是满二叉树；

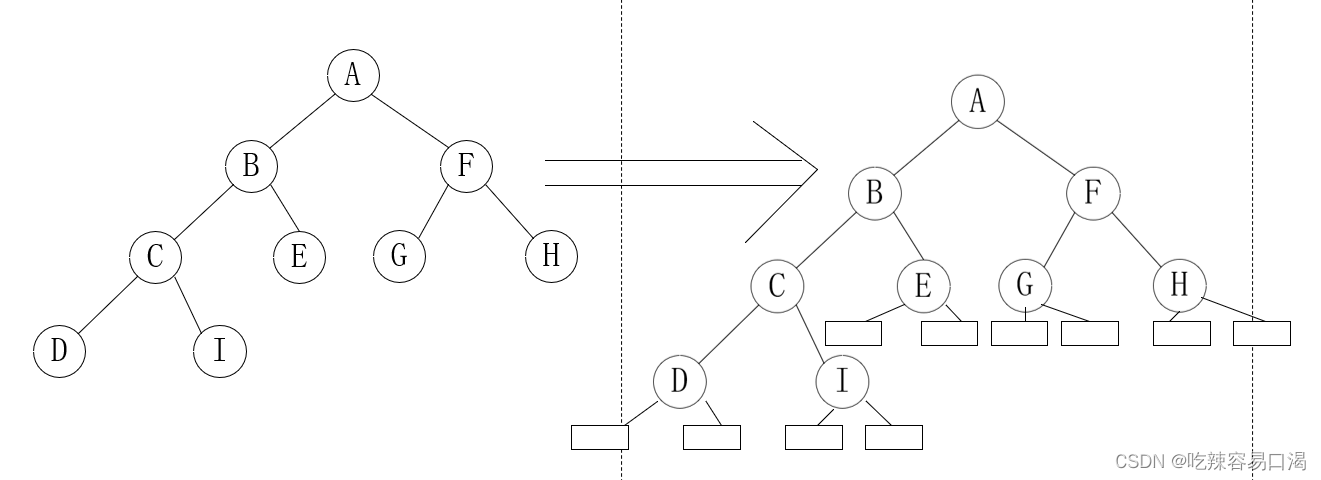
3、扩充二叉树

扩充二叉树是对已有二叉树的扩充，扩充后的二叉树的节点都变为度数为2的分支节点。也就是说，如果原节点的度数为2，则不变，度数为1，则增加一个分支，度数为0的叶子节点则增加两个分支。将二叉树的结点全部都加上结点

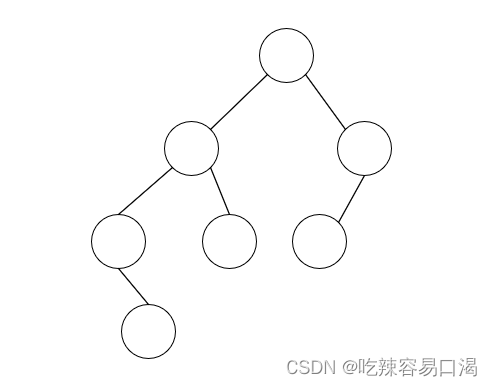
4、平衡二叉树

是一棵空树或它的任意节点的左右两个子树的高度差的绝对值不超过1

二叉树的应用场景

普通的二叉树，很难构成现实的应用场景，但因其简单，常用于学习研究，平衡二叉树则是实际应用比较多的。常见于快速匹配、搜索等方面。
常用的树有：AVL树、红黑树、B+树、Trie（字典）树。
1、AVL树: 最早的平衡二叉树之一。应用相对其他数据结构比较少。windows对进程地址空间的管理用到了AVL树。
2、红黑树: 平衡二叉树，广泛用在C++的STL中。如map和set都是用红黑树实现的。还有Linux文件管理。
3、B/B+树: 用在磁盘文件组织 数据索引和数据库索引。
4、Trie树(字典树): 用在统计和排序大量字符串，如自动机、M数据库索引。

遍历方式

1、先序排列

2、中序遍历

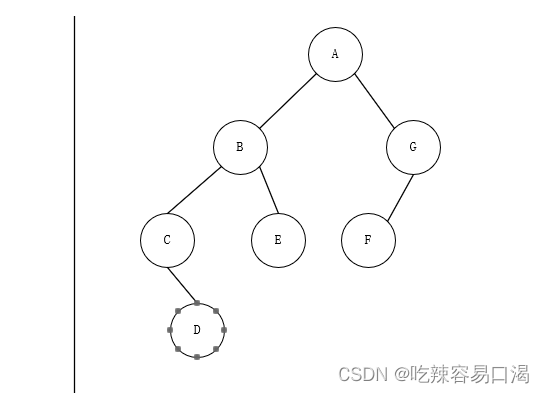
从左往右依次遍历遍历结果为：
CDBEAFG

3、后序遍历

围绕着外圈依次开始遍历（先记录的是最下面的），然后依次记录
DICEBGHFA

4、层次遍历

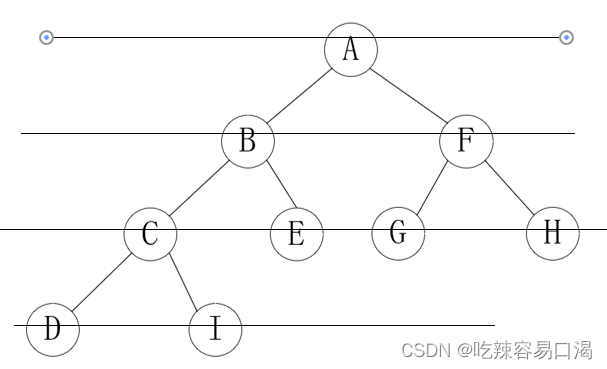
从根节点开始，一层一层，从下往上，每层从左至右。
DICEGHBFA

代码实现

package tree;

import java.util.Stack;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;


public class BianLi {
    static class TreeNode {
        public int val;//数据
        public TreeNode left;//左孩子的引用，常常代表左孩子为根的整棵左子树
        public TreeNode right;// 右孩子的引用，常常代表右孩子为根的整棵右子树

        public TreeNode(int val) {
            this.val = val;
        }
    }
    public static void main(String[] args) {
        //构造树结构测试用
        TreeNode a = new TreeNode(1);
        TreeNode b = new TreeNode(2);
        TreeNode c = new TreeNode(3);
        TreeNode d = new TreeNode(4);
        TreeNode e = new TreeNode(5);
        TreeNode f = new TreeNode(6);
        TreeNode g = new TreeNode(7);
        a.left = b;
        a.right = c;
        b.right = d;
        c.left = e;
        c.right = f;
        f.left = g;
        System.out.print("recursivePreOrder: ");
        recursivePreOrder(a);
        System.out.print('\n' + "recursiveInOrder: ");
        recursiveInOrder(a);
        System.out.print('\n' + "recursivePostOrder: ");
        recursivePostOrder(a);
        System.out.print('\n' + "iterativePreOrder: ");
        iterativePreOrder(a);
        System.out.print('\n' + "iterativePreOrder_2: ");
        iterativePreOrder_2(a);
        System.out.print('\n' + "iterativeInOrder: ");
        iterativeInOrder(a);
        System.out.print('\n' + "iterativePostOrder: ");
        iterativePostOrder(a);
        System.out.print('\n' + "iterativePostOrder_2: ");
        iterativePostOrder_2(a);
        System.out.print('\n' + "iterativePostOrder_3: ");
        iterativePostOrder_3(a);
        System.out.print('\n' + "iterativeLevelOrder: ");
        iterativeLevelOrder(a);
        System.out.print('\n' + "iterativeLevelOrder_2: " + '\n');
        iterativeLevelOrder_2(a);
        System.out.print('\n' + "recursiveLevelOrder: ");
        recurLevelOrder(a);
        System.out.print('\n' + "recursiveLevelOrderBottom: " + '\n');
        List<List<Integer>> lists = recursiveLevelOrderBottom(a);
        for (List<Integer> list : lists) {
            for (int p : list) {
                System.out.print(p + " ");
            }
            System.out.println();
        }
    }


    /**
     * 输出值
     * @param p
     */
    public static void visit(TreeNode p) {
        System.out.print(p.val + " ");
    }

    /**
     *先序遍历
     * @param p
     */
    public static void recursivePreOrder(TreeNode p) {
        if (p == null) return;
        visit(p);
        recursivePreOrder(p.left);
        recursivePreOrder(p.right);
    }

    /**
     * 中序遍历
     * @param p
     */
    public static void recursiveInOrder(TreeNode p) {
        if (p == null) return;
        recursiveInOrder(p.left);
        visit(p);
        recursiveInOrder(p.right);
    }

    /**
     * 后序遍历
     * @param p
     */
    public static void recursivePostOrder(TreeNode p) {
        if (p == null) return;
        recursivePostOrder(p.left);
        recursivePostOrder(p.right);
        visit(p);
    }


    //**********非递归的先序遍历**********
    //手算的思想，先变访问边找，找到最左下方的，然后向上再向访问右边的

    public static void iterativePreOrder(TreeNode p) {
        if (p == null) return;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while (!stack.empty() || p != null) {
            while (p != null) {
                visit(p);
                stack.push(p);
                p = p.left;
            }
            p = stack.pop();
            p = p.right;
        }
    }

    //**********非递归的先序遍历**********
    //栈的思想，按层次倒着进栈，利用后进先出解决顺序问题
    public static void iterativePreOrder_2(TreeNode p) {
        if (p == null) return;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(p);
        while (!stack.empty()) {
            p = stack.pop();
            visit(p);
            if (p.right != null) stack.push(p.right);
            if (p.left != null) stack.push(p.left);
        }
    }


    //**********非递归的中序遍历**********
    public static void iterativeInOrder(TreeNode p) {
        if (p == null) return;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        while (!stack.empty() || p != null) {
            while (p != null) {
                stack.push(p);
                p = p.left;
            }
            p = stack.pop();
            visit(p);
            p = p.right;
        }
    }


    //**********非递归的后序遍历**********
    //注意prev的作用
    public static void iterativePostOrder(TreeNode p) {
        if (p == null) return;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode prev = p;
        while (!stack.empty() || p != null) {
            while (p != null) {
                stack.push(p);
                p = p.left;
            }
            p = stack.peek().right;
            if (p == null || p == prev) {
                //若栈顶节点的右节点为空或者已经visit过，则按顺序应该访问栈顶节点
                p = stack.pop();
                visit(p);
                //prev用来标记已经visit过这个节点
                prev = p;
                p = null;
            }
        }
    }


    //**********非递归的后序遍历**********
    //和上一种方法思想类似
    public static void iterativePostOrder_2(TreeNode p) {
        if (p == null) return;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode prev = p;
        while (p != null) {
            while (p.left != null) {
                stack.push(p);
                p = p.left;
            }
            while (p != null && (p.right == null || p.right == prev)) {
                visit(p);
                prev = p;
                if (stack.empty()) return;
                p = stack.pop();
            }
            stack.push(p);
            p = p.right;
        }
    }


    //**********非递归的后序遍历**********
    //双栈法，易于理解
    public static void iterativePostOrder_3(TreeNode p) {
        if (p == null) return;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        Stack<TreeNode> result = new Stack<TreeNode>();
        while (!stack.empty() || p != null) {
            while (p != null) {
                stack.push(p);
                result.push(p);
                p = p.right;
            }
            if (!stack.empty()) p = stack.pop().left;
        }
        while (!result.empty()) {
            p = result.pop();
            visit(p);
        }
    }


    //**********非递归的层次遍历**********
    public static void iterativeLevelOrder(TreeNode p) {
        if (p == null) return;
        LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(p);
        while (!queue.isEmpty()) {
            p = queue.poll();
            if (p.left != null) queue.offer(p.left);
            if (p.right != null) queue.offer(p.right);
            visit(p);
        }
    }


    //**********非递归的分层输出的层次遍历**********
    public static void iterativeLevelOrder_1(TreeNode p) {
        if (p == null) return;
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(p);
        while (!queue.isEmpty()) {
            int levelNum = queue.size();
            for (int i = 0; i < levelNum; i++) {
                p = queue.poll();
                if (p.left != null) queue.offer(p.left);
                if (p.right != null) queue.offer(p.right);
                visit(p);
            }
            System.out.println();
        }
    }


    //**********非递归的分层输出的层次遍历**********
    //维护两个int，代表上一层和下一层的节点数量，上一层遍历结束之后lineUp = lineDown; lineDown = 0;
    public static void iterativeLevelOrder_2(TreeNode p) {
        if (p == null) return;
        LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
        int lineUp = 1, lineDown = 0;
        queue.offer(p);
        while (!queue.isEmpty()) {
            p = queue.poll();
            visit(p);
            if (p.left != null){
                queue.offer(p.left);
                lineDown++;
            }
            if (p.right != null){
                queue.offer(p.right);
                lineDown++;
            }
            if (--lineUp == 0) {
                lineUp = lineDown;
                lineDown = 0;
                System.out.println();
            }
        }
    }


    //**********递归的层次遍历访问**********
    public static void recurLevelOrder(TreeNode root) {
        if (root == null) return;
        int depth = maxDepth(root);
        //如果要倒序访问只需修改此处顺序
        for (int i = 1; i <= depth; i++) visitNodeAtDepth(root, i);
    }
    //访问特定层的节点
    public static void visitNodeAtDepth(TreeNode p, int depth) {
        if (p == null || depth < 1) return;
        //因为要按顺序访问（打印），所以要规定必须到某一层才能visit
        if (depth == 1) {
            visit(p);
            return;
        }
        //每次都要遍历depth之上的所有层
        visitNodeAtDepth(p.left, depth - 1);
        visitNodeAtDepth(p.right, depth - 1);
    }
    //得到树的层数
    public static int maxDepth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }


    //**********递归的倒序层次遍历并保存结果至list**********
    //LeetCode107
    //之所以用LinkedList是因为有addFirst()方法，可以逆序保存
    public static List<List<Integer>> recursiveLevelOrderBottom(TreeNode root) {
        LinkedList<List<Integer>> lists = new LinkedList<List<Integer>>();
        addToList(lists, root, 1);
        return lists;
    }
    //将depth层的p节点保存至list
    public static void addToList(LinkedList<List<Integer>> lists, TreeNode p, int depth) {
        if (p == null) return;
        if (lists.size() < depth) lists.addFirst(new LinkedList<Integer>());
        //由于不用输出只是保存，可以使用get控制保存在哪一层，所以不用规定层数
        lists.get(lists.size() - depth).add(p.val);
        addToList(lists, p.left, depth + 1);
        addToList(lists, p.right, depth + 1);
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330