【ML01】Linear Regression with One Variable

（一）概述

在机器学习中，主要分为 监督学习(Supervised Learning)、非监督学习(Unsupervised Learning) 以及 强化学习(Reinforcement Learning)。而在监督学习中，主要分为两大类，回归(Regression) 以及 分类(Classification) 模型。

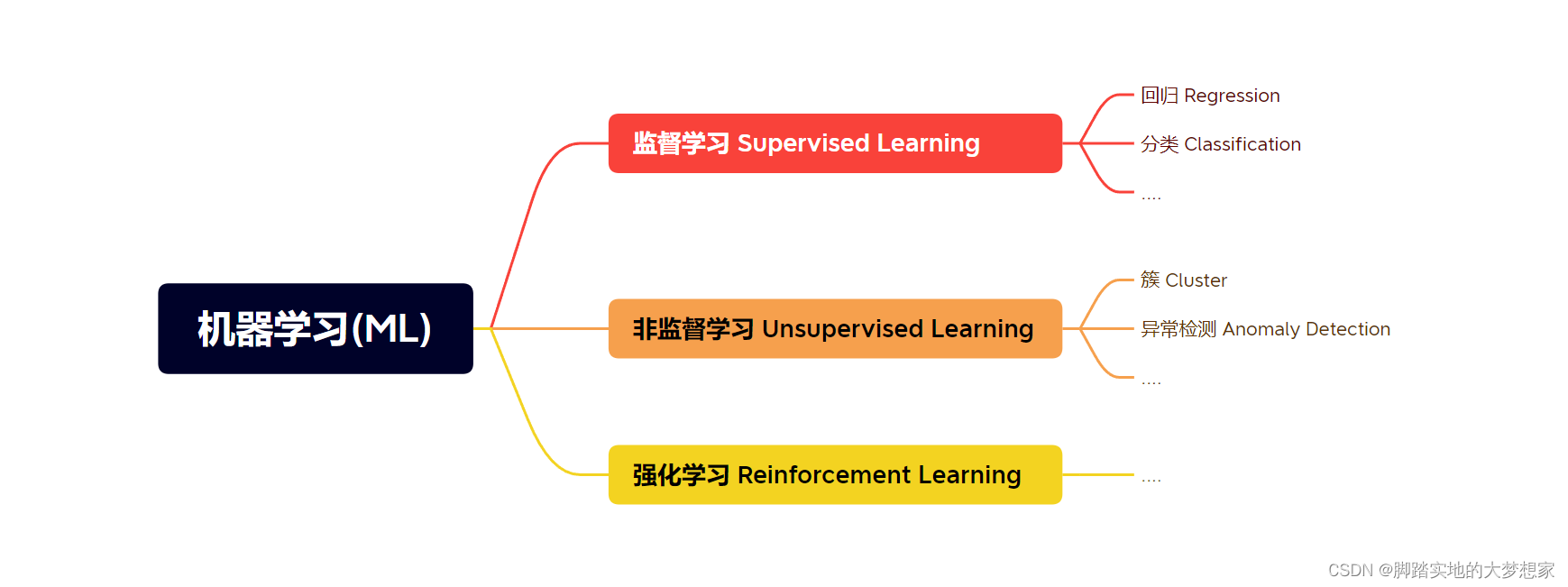
线性回归，当然属于 监督学习-回归模型，且为很多解决当下现实问题用到。
思考来看，线性回归问题与方程式类似，原理都为给定带有权重的自变量，根据函数算法计算其预测值。其中核心在于选择合适的算法，即function。

---

（二）notation

Linear Regression with only one variable:
$$f_{\mathbf{w},\mathbf{b}}(\mathbf{x})=wx+b$$
其中：

---

（三）流程 Process

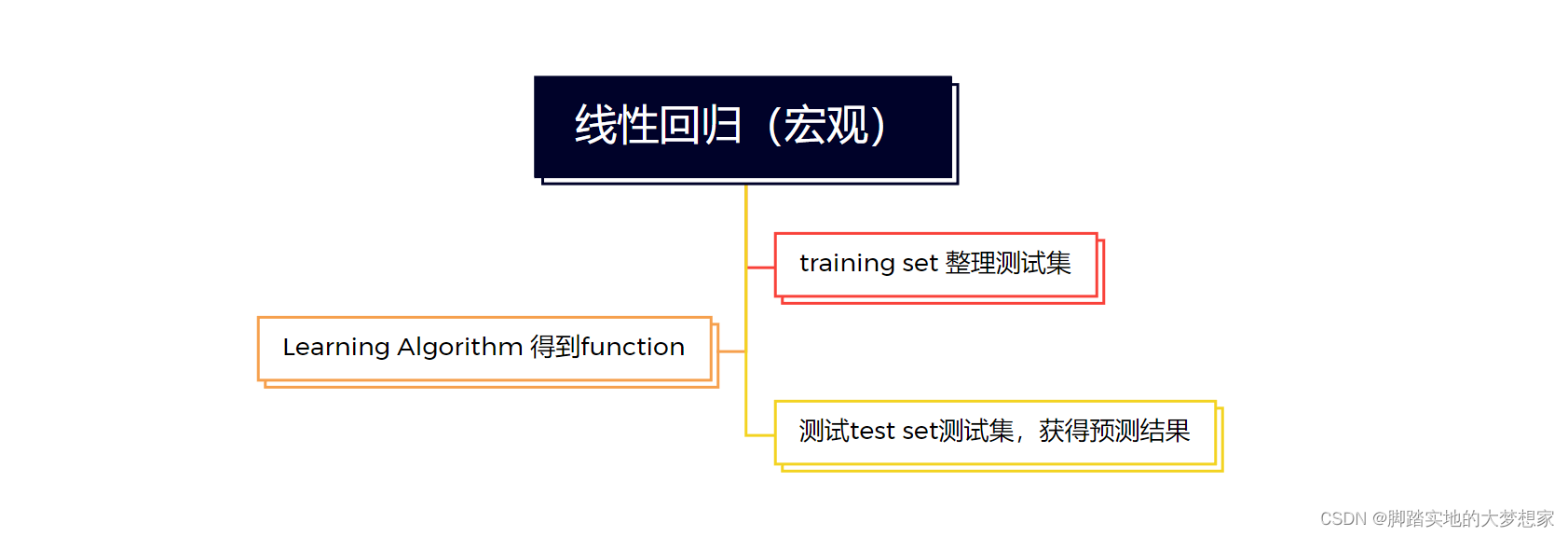
首先，第一步将 数据集(dataset) 分为两个部分，训练集(training set) 以及 测试集(test set)。通常按照 8：2 的方式进行划分，当然训练集占大数；

第二步，将训练集带入到线性回归函数中，得到线性回归函数；

第三步，将训练好的回归函数测试测试集中数据，通过输入自变量得到预测值，通过：[实际值-预测值]² 等方式得到 cost function，从而判断回归函数是否符合要求。

---

（四）python搭建一个最基本的线性回归模型

@@------@@
4.1 问题陈述
@@------@@

通过线性回归函数预测房价，拥有训练集如下：

@@------------------@@
4.2 numpy建立数据集
@@------------------@@

import numpy as np

x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
print(f"x_train = {x_train}")		# 打印训练集中自变量
print(f"y_train = {y_train}")		# 打印训练集中因变量

i = 1								# 打印训练集中第i个自变量因变量 
x_i = x_train[i]
y_i = y_train[i]
print(f"(x^({i}), y^({i})) = ({x_i}, {y_i})")

print(f"x_train.shape: {x_train.shape}")		# 打印训练集中自变量的数量
print(f"Number of training examples is: {m}")	# 打印训练集中因变量的数量

m = len(x_train)
print(f"Number of training examples is: {m}")	# 打印训练集的长度，换一种方法打印训练集的数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

@@---------@@
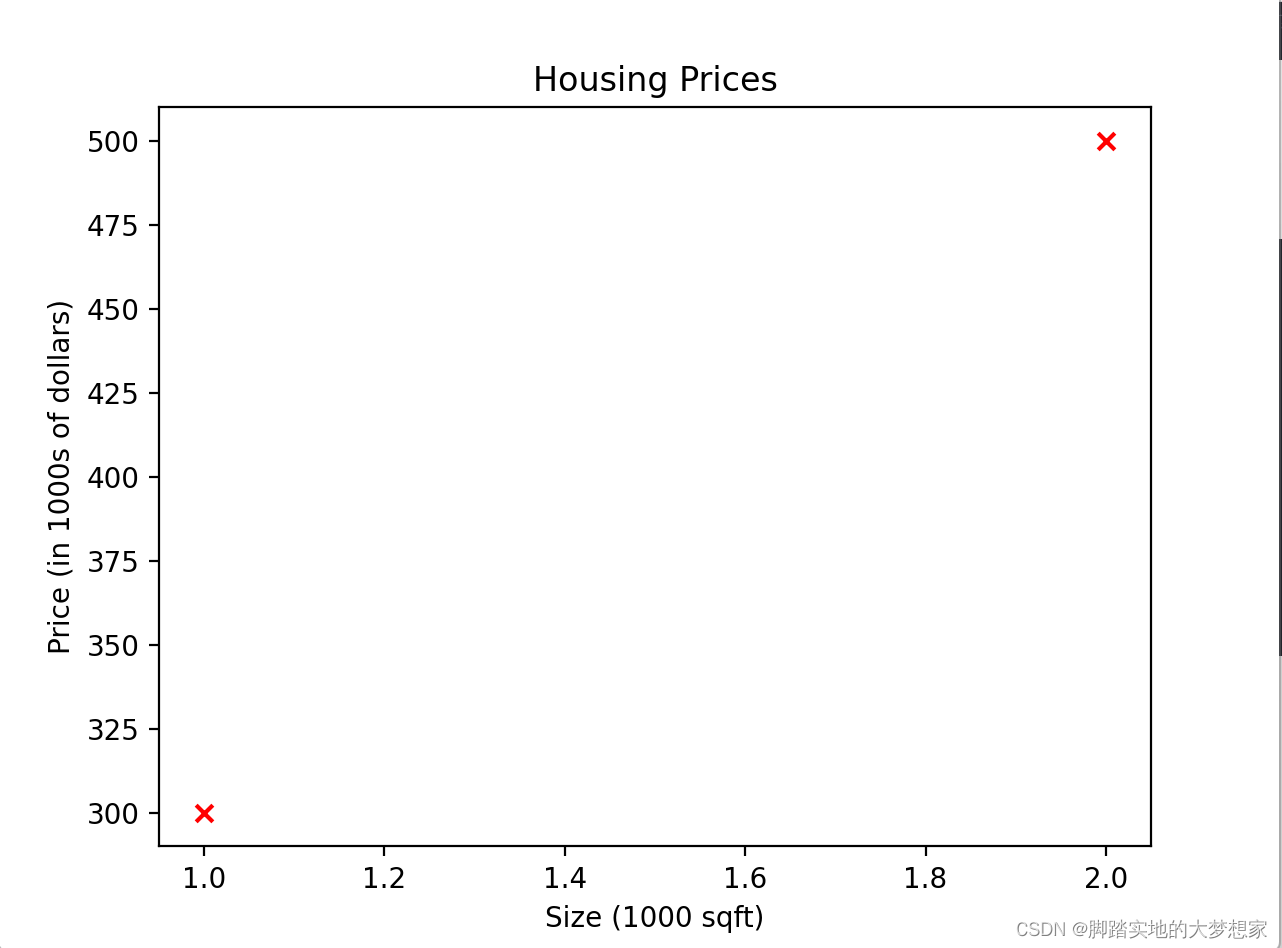
4.3 plt绘制数据
@@---------@@

import numpy as np
import matplotlib.pyplot as plt

x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])

# 字面意思，自行理解。
plt.scatter(x_train, y_train, marker='x', c='r')
plt.title("Housing Prices")
plt.ylabel('Price (in 1000s of dollars)')
plt.xlabel('Size (1000 sqft)')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

@@-------------------@@
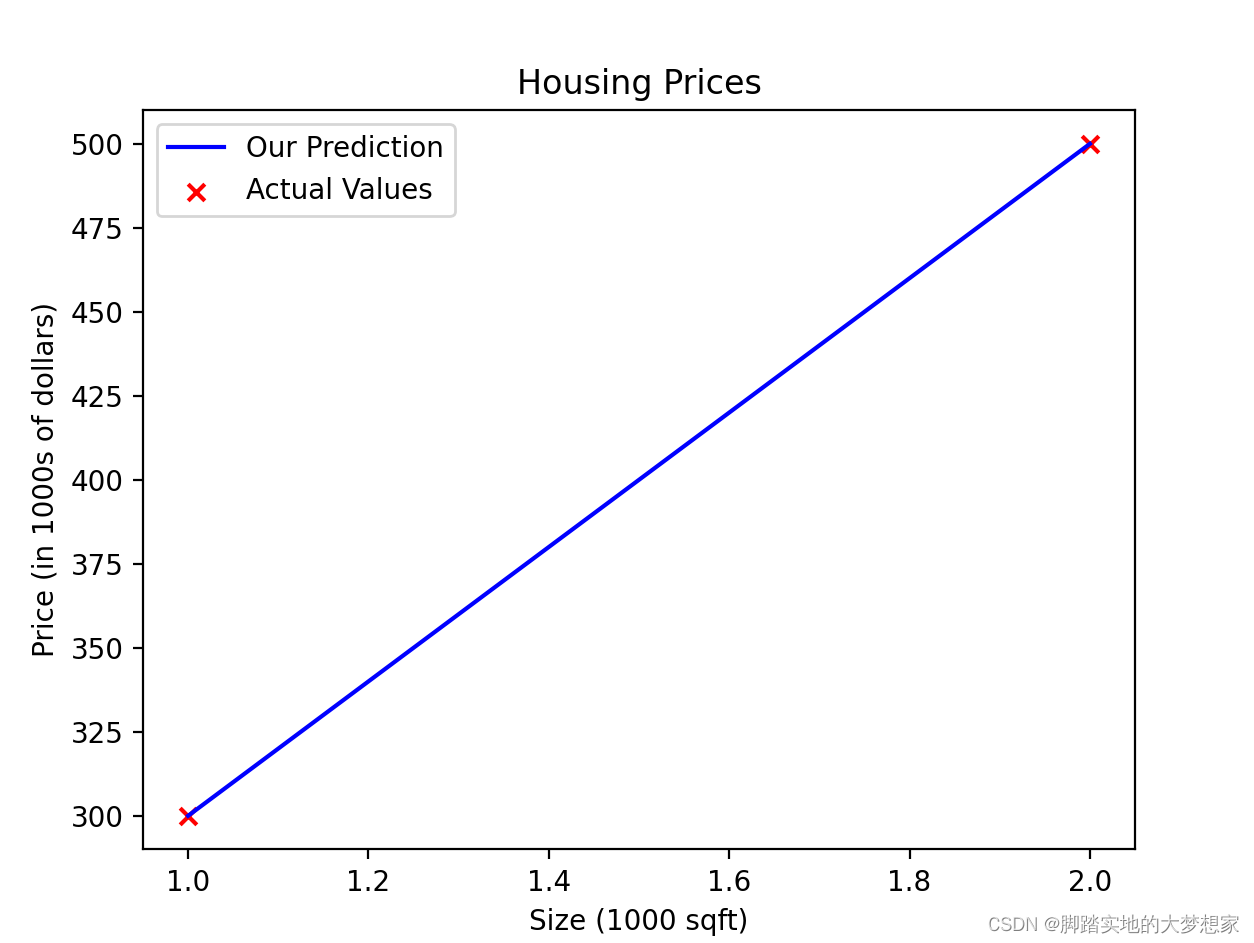
4.4 结合w,b值绘制函数
@@-------------------@@

Linear Regression Fuction：
$$f_{w,b}(x^{(i)})=w{x}^{(i)}+b\text{\hspace{1em}(1)}$$

if w=200, b=100

import numpy as np
import matplotlib.pyplot as plt

w = 200
b = 100
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
m = x_train.shape[0]
f_wb = np.zeros(m)		# 创建全为0的零向量m
for i in range(m):
	f_wb[i] = w * x_train[i] + b
	
plt.plot(x_train, f_wb, c='b',label='预测值')
plt.scatter(x_train, y_train, marker='x', c='r',label='实际值')
plt.title("Housing Prices")
plt.ylabel('Price (in 1000s of dollars)')
plt.xlabel('Size (1000 sqft)')
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

@@---------------------------@@
4.5 预测1200尺时房子的价格
@@---------------------------@@

w = 200
b = 100
x_i = 1.2
cost_1200sqft = w * x_i + b    
print(f"${cost_1200sqft:.0f} thousand dollars")
1
2
3
4
5

测试案例来源于 吴恩达《Machine Learning》Model representation
仅供学习参考

end ---- >