JZ23 链表中环的入口结点

题目：
给一个长度为n链表，若其中包含环，请找出该链表的环的入口结点，否则，返回null。

解法一：哈希表
用哈希表将访问过的节点存储起来，如果遇到重复的节点，说明就是环的入口，返回该节点即可。

public ListNode EntryNodeOfLoop(ListNode pHead) {
        Set<ListNode> set = new HashSet<>();
        while (pHead != null) {
            if (set.contains(pHead)) {
                return pHead;
            } else {
                set.add(pHead);
                pHead = pHead.next;
            }
        }
        return null;
    }

复杂度分析：
时间复杂度：O(n)，遍历链表一次
空间复杂度：O(n)，存储遍历的n个链表节点

解法二：快慢双指针
主要是数学分析，代码不难。
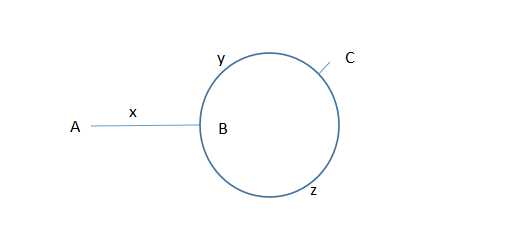
首先分析链表是否有环，构造快慢两个指针，快指针步幅为2，慢指针步幅为1。如果有环，则快慢指针一定会相遇，且快指针所走的路径等于慢指针所走的路径2倍，假设它们在下图中的C的相遇，相遇时快指针在环里走了n圈，慢指针在环里走了m圈，则：
快指针走的路径：x+n(y+z)+y
慢指针走的路径：x+m(y+z)+y
且存在对应关系：x+n(y+z)+y=2(x+m(y+z)+y),化简可得：x+y=(n-2m)(y+z)。x+y为从链表头部到相遇点的距离，y+z为环的长度，可得从链表头部到相遇点的距离是环的长度的整数倍。那快慢以相同的步幅，快指针从链表头开始遍历，慢指针继续在环中遍历，快慢指针最终还是会在C点相遇，因为他们步幅相同，所以其实在B点就已经相遇，然后从B点开始，快慢指针携手并进，一直在环内手拉手走到天荒地老。

    public ListNode EntryNodeOfLoop(ListNode pHead) {
        ListNode slow = hasCircle(pHead);
        if (slow == null) {
            return null;
        }
        ListNode fast = pHead;
        while (fast != slow) {
            fast = fast.next;
            slow = slow.next;
        }
        return fast;
    }

    private ListNode hasCircle(ListNode pHead) {
        if (pHead == null) {
            return null;
        }
        ListNode fast = pHead;
        ListNode slow = pHead;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                return slow;
            }
        }
        return null;
    }

先判断链表是否有环，采用步幅不同的快慢指针，若相遇则有环。
寻找环的入口，返回相遇时的节点，然后快指针从链表头开始，慢指针从相遇点开始，以相同步幅遍历，相遇点即是入口。

复杂度分析：
时间复杂度：O(n)
空间复杂度：O(1)

总结：
涉及数据结构：链表、哈希表
涉及算法：快慢双指针