-
【数据结构与算法】快速排序算法、归并排序算法的介绍和程序实现
1. 快速排序算法
1.1 快速排序的介绍
快速排序(Quicksort)是对冒泡排序的一种改进
基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
1.2 快速排序的程序实现
需求:有一组无序的数据{-9,78,0,23,-567,70, -1,900, 4561}; ,请用快速排序算法实现从小到大排列
程序如下:
import java.util.Arrays; public class QuickSort { public static void main(String[] args) { int[] array = {-9, 78, 0, 23, -567, 70, -1, 900, 4561}; // left和right分别是此次快速排序递归的开始index和结束index quickSort(array, 0, array.length - 1); System.out.println("array = " + Arrays.toString(array)); } // array是多次递归共用的,left和right分别是此次快速排序递归的开始index和结束index public static void quickSort(int[] array, int left, int right) { int tmpLeft = left; int tmpRight = right; // 临时的中轴值。注意tmpPivot的值随着交换,其对应的index会不断的发生变化 // 但是最终的目的是让其index右边的值比tmpPivot大,左边的值比tmpPivot小 int tmpPivot = array[(left + right) / 2]; // 交换时的临时变量 int tmp = 0; // 不断进行遍历,让tmpPivot对应的index的右边的值比tmpPivot大,左边的值比tmpPivot小 // 只有当tmpLeft小于tmpRight才有必要进行值交换 while (tmpLeft < tmpRight) { // 不断的进行查找,直到在tmpPivot对应index左边的值比tmpPivot大的值,则退出,等待值交换 // tmpLeft不会大于tmpPivot所在index while (array[tmpLeft] < tmpPivot) { tmpLeft += 1; } // 不断的进行查找,直到在在tmpPivot对应index右边的值比tmpPivot小的值,则退出,等待值交换 // tmpRight不会小于tmpPivot所在index while (array[tmpRight] > tmpPivot) { tmpRight -= 1; } // 如果l == r说明tmpPivot对应index的左边的值都比tmpPivot小,右边的值都比tmpPivot大 // 直接进行退出,不用再进行值交换 if (tmpLeft == tmpRight) { break; } // 进行左右两边的值交换。可能会将tmpPivot的值也进行交换 tmp = array[tmpLeft]; array[tmpLeft] = array[tmpRight]; array[tmpRight] = tmp; // 当tmpLeft所在index的值比tmpPivot(tmpRight所在index的值)大 // 进行值交换后,此时tmpRight所在index的值比tmpPivot所在index的值大,tmpRight所在index不用再参与这一轮比较 // 所以需要将tmpRight前移,以便后续的值交换 if (array[tmpLeft] == tmpPivot) { tmpRight -= 1; } // 当tmpRight所在index的值比tmpPivot(tmpLeft所在index的值)小 // 进行值交换后,此时tmpLeft所在index的值比tmpPivot所在index的值小,tmpLeft所在index不用再参与这一轮比较 // 所以需要将tmpLeft后移,以便后续的值交换 if (array[tmpRight] == tmpPivot) { tmpLeft += 1; } } // 如果tmpLeft == tmpRight, 将tmpLeft后移,tmpRight前移,使后续的递归调用index不重叠 if (tmpLeft == tmpRight) { tmpLeft += 1; tmpRight -= 1; } // 向左递归 if (left < tmpRight) { quickSort(array, left, tmpRight); } // 向右递归 if (right > tmpLeft) { quickSort(array, tmpLeft, right); } } }运行程序,结果如下:
array = [-567, -9, -1, 0, 23, 70, 78, 900, 4561]2. 归并排序算法
2.1 归并排序的介绍
归并排序(merge-sort)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)
归并排序的思想如下所示:
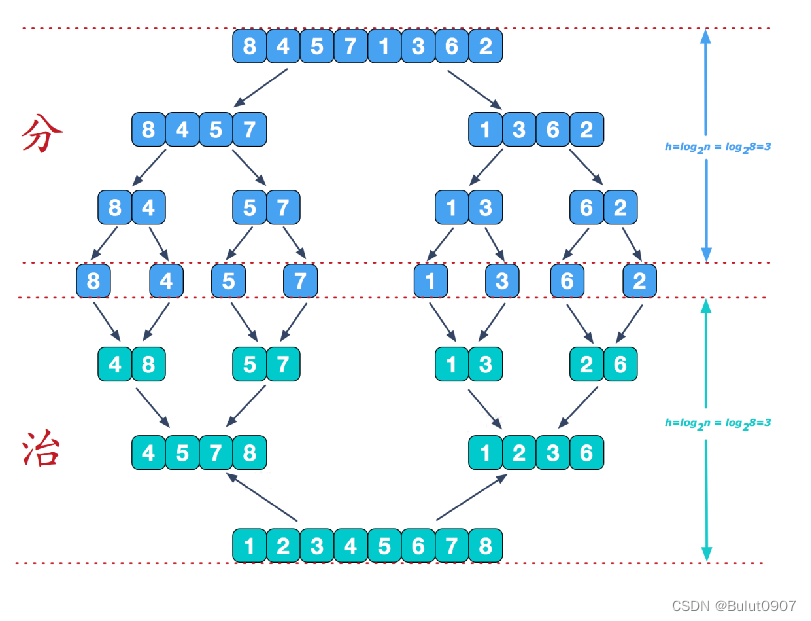
归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程。而治阶段,需要将两个已经内部有序外部无序的子序列合并成一个有序序列2.2 归并排序的程序实现
需求:有一组无序的数据{8, 4, 5, 7, 1, 3, 6, 2},请用归并排序算法实现从小到大排列
程序如下:
import java.util.Arrays; public class MergeSort { public static void main(String[] args) { int[] array = {8, 4, 5, 7, 1, 3, 6, 2}; // 用来保存合并后的有序序列的临时数组, 供每次合并使用,大小和原始数组一样大 int[] tmpArray = new int[array.length]; mergeSort(array, 0, array.length - 1, tmpArray); System.out.println("归并排序后 = " + Arrays.toString(array)); } // 归并排序实现。先进行拆分,再进行合并 public static void mergeSort(int[] array, int left, int right, int[] tmpArray) { // 当拆分后只有一个元素时,left == right,就不再进行拆分,拆分完成 if (left < right) { int mid = (left + right) / 2; // 向左递归进行拆分 mergeSort(array, left, mid, tmpArray); // 向右递归进行拆分 mergeSort(array, mid + 1, right, tmpArray); // 等左右都拆分完成。开始对左右进行合并 // 合并前左边的是有序的,右边的也是有序的,但左右无序,合并后的数据是有序的 // 然后不断的进行回溯 merge(array, left, mid, right, tmpArray); } } /* 各参数含义: array:原始的数组 left:合并前的左边有序序列的开始index right:合并前左右有序序列的中间index right:合并前右边有序序列的结束index tmpArray:用来保存合并后的有序序列的临时数组 */ public static void merge(int[] array, int left, int mid, int right, int[] tmpArray) { // 左边有序序列的第一个index int tmpLeft = left; // 右边有序序列的第一个index int tmpRight = mid + 1; int tmpArrayIndex = 0; // 同时遍历左边有序序列,和右边有序序列 while (tmpLeft <= mid && tmpRight <= right) { // 如果左边有序序列的值小,则将左边有序序列的值保存到tmpArray,然后将左边有序序列的index后移 // tmpArray保存的是左右两个有序序列的较小值 if (array[tmpLeft] <= array[tmpRight]) { tmpArray[tmpArrayIndex] = array[tmpLeft]; tmpArrayIndex += 1; tmpLeft += 1; } else { // 如果右边有序序列的值小,则将右边有序序列的值保存到tmpArray,然后将右边有序序列的index后移 // tmpArray保存的是左右两个有序序列的较小值 tmpArray[tmpArrayIndex] = array[tmpRight]; tmpArrayIndex += 1; tmpRight += 1; } } // 当右边的有序序列都保存到tmpArray中,将左边有序序列的剩余元素依次保存到tmpArray while (tmpLeft <= mid) { tmpArray[tmpArrayIndex] = array[tmpLeft]; tmpArrayIndex += 1; tmpLeft += 1; } // 当左边的有序序列都保存到tmpArray中,将右边有序序列的剩余元素依次保存到tmpArray while (tmpRight <= right) { tmpArray[tmpArrayIndex] = array[tmpRight]; tmpArrayIndex += 1; tmpRight += 1; } // 将tmpArray此次保存的数据,重新赋值给array对应index范围 // 使array对应index范围的数据,由无序序列变成一个有序序列,便于后续的合并 tmpArrayIndex = 0; int copy2ArrayLeft = left; while (copy2ArrayLeft <= right) { array[copy2ArrayLeft] = tmpArray[tmpArrayIndex]; tmpArrayIndex += 1; copy2ArrayLeft += 1; } } }运行程序,结果如下:
归并排序后 = [1, 2, 3, 4, 5, 6, 7, 8] -
相关阅读:
【ML特征工程】第 5 章 :分类变量:机器鸡时代的鸡蛋计数
黑马JVM总结(十一)
苍穹外卖01-项目概述、环境搭建
【软键盘】Android开发之隐藏软键盘的方式
基于javaweb简单的在线考试系统
tars架构
Cy3/5/7标记多肽/PEG/聚合物/磷脂----为华生物
vue2+element-ui实现表格分页显示
代码随想录算法训练营第四天 | 24. 两两交换链表中的节点、19.删除链表的倒数第N个节点、160.链表相交、142.环形链表II
AXI协议详解(7)-响应信号
- 原文地址:https://blog.csdn.net/yy8623977/article/details/126698969