数据结构之堆

一、什么是堆

（一）堆的定义

一个大小为 n 的堆（heap） 是一棵包含 n 个结点的 完全二叉树，其根节点称为堆顶，根据堆中亲自结点的大小关系，堆可以分为两类。
（1）最小堆：如果树中每个结点的元素都小于或等于其孩子结点的元素，则称该堆为最小堆。
在最小堆中，堆顶存储的元素是整棵树中最小的。
（2）最大堆：如果树中每个结点的元素都大于或等于其孩子结点的元素，则称该堆为最大堆。
在最大堆中，堆顶存储的元素是整棵树中最小的。

（二）堆的存储结构

堆的逻辑结构是树形结构，并且是一种特殊的树形结构——完全二叉树。对于堆而言，在物理存储上仍然采用的是顺序存储表示。

堆是包含n个元素的序列$(k_0,k_1,...,k_{n-1})$，堆顶元素和堆底元素分别为序列的第一个元素 和最后一个元素。最大堆和最小堆 的条件要求如下：
当且仅当 $$k_i\le k_{2i+1}且k_i\le k_{2i+2}(i=0,1,...,\lfloor (n-2)/2\rfloor )$$ 时，该序列称为最小堆；

当且仅当 $$k_i\ge k_{2i+1}且k_i\ge k_{2i+2}(i=0,1,...,\lfloor (n-2)/2\rfloor )$$ 时，该序列称为最大堆。

下面给了最小堆和最大堆的两个例子。

---

---

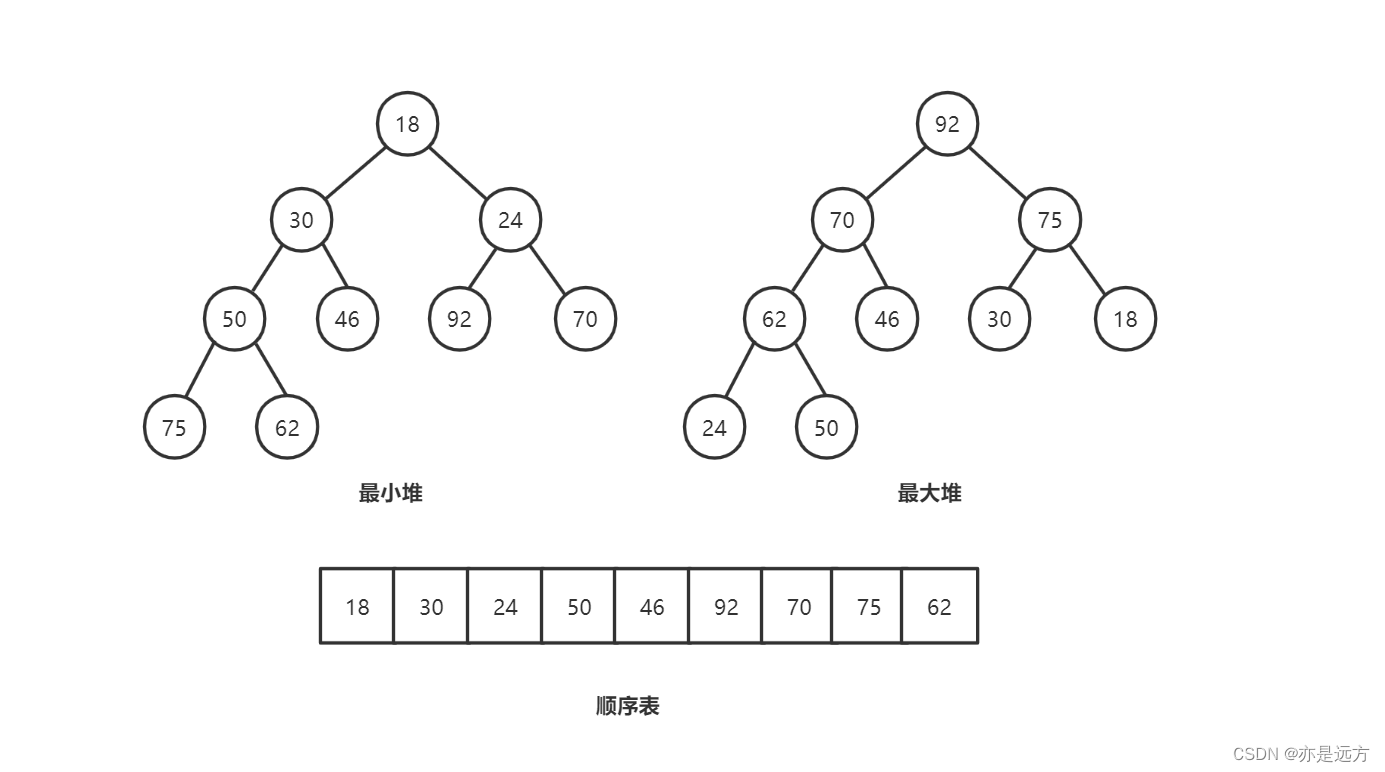
二、怎么建立一个堆

（一）AdjustDown算法

在一棵完全二叉树中，由于所有的叶子结点没有孩子，所以这些叶子结点一定满足堆的要求，无需进行调整。
对于完全二叉树的非叶子节点，需要执行建堆得向下调整算法 AdjustDown。

（二）AdjustDown算法详解

向下调整算法的函数定义如下：
$$voidAdjustDown(ElemTypeheap[],intcurrent,intborder)$$

其中 ， current 表示当前待调整的目标元素在以数组 heap 表示的完全二叉树中的位置， border 表示完全二叉树的下边界位置，即最后一个 元素所在的位置；并且， heap 从位置 current+1 到位置 border 之间的这 border - current 个元素都满足：其中的任一元 素要么不存在孩子结点，要 么该 元素不大千其孩子结点中的元素，也就是说 heap 中的这 border- current 个元素都符合最小堆的要求。此时，执行 AdjustDown 操作将使得 heap 中增加一个满足最小堆的要求的元素（ 即heap[current]）。

实现向下调整运算 AdjustDown 的具体方法如下：首先，设置结点指针 p 指向当前考查元素heap[current]，即 p =current ; 接着启动循环调整过程，如果 p 指向的元 素 heap[p] 大千其左、右孩子中的较小者（即 heap[2*p + 1] 和 heap[2*p＋2］ 中的较小的元 素），则将 heap[p] 与其较小孩子交换，并设 置 p 指向原先较小孩 子当前所在的位置（此时该位置中存储的依然是原先的当前考查元素， 也就是说 p 指向的元 素并没有发生变化 ），然 后继续执行下一轮的循环。在循环过程中，如 果发 现 p 指向的 元素 heap[p] 不大于其左、右孩子中的较小者， 或 者 p 已 到达叶结点 ，则本轮向下调整结束。

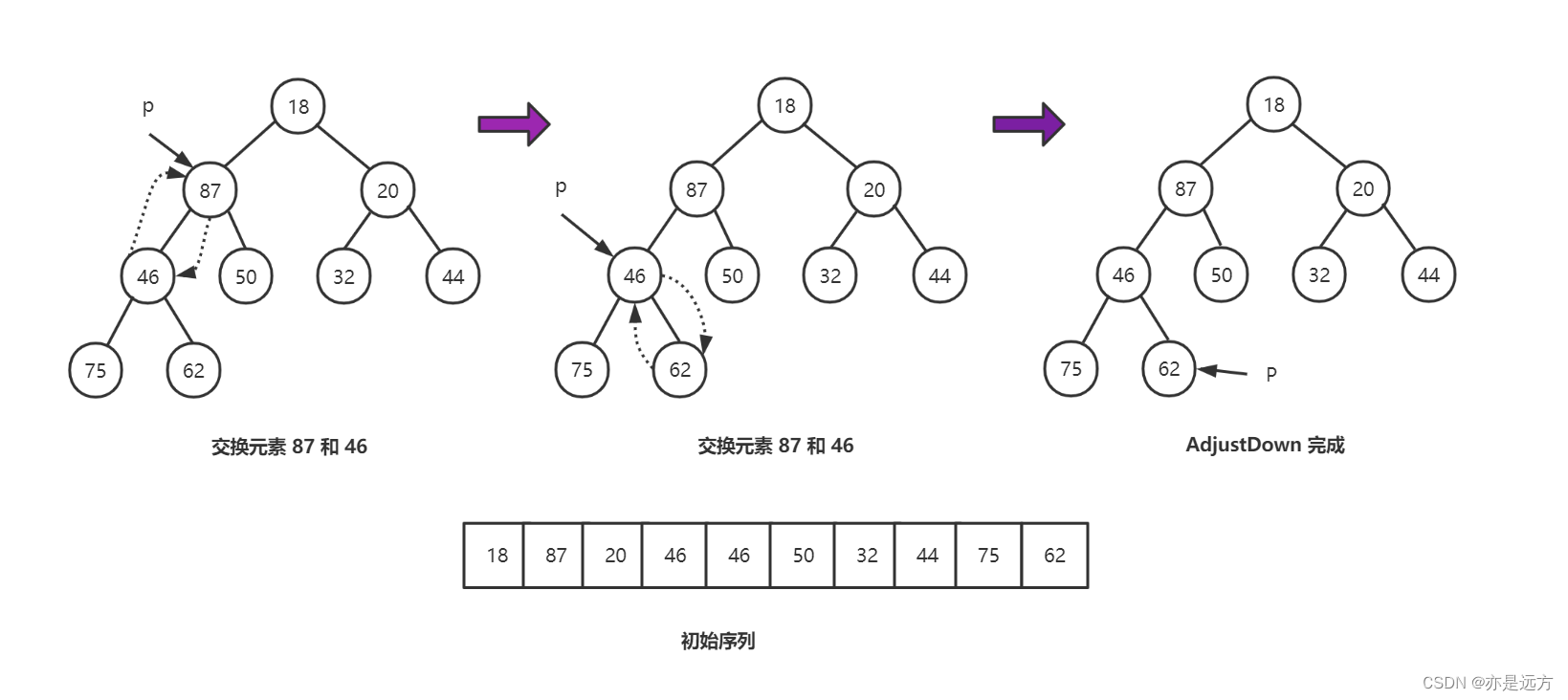
下面给出了序列 heap={18, 87, 20, 46, 50, 32, 44, 75, 62} 的建堆过程。
显然当前的 heap[2], heap[3] ,… , heap[8] 已满足最小堆的条件要求， 即这些元素都不大于它们的孩 子结点；当 前需 执行向下 调 整 的 目标对象 为 p=1 指向的元素heap[1]=87，调 整 过程如图由于 heap[1] 大于其较小的孩子 heap[3]=46, 所以首先将 heap[1] 与 heap[3] 交换， 交 换后的heap如图 5.27 ( b ) 所示，此时 p 指向 heap[3]=87; 继续比较 p 指向的元索 heap[3] 和其较小孩子heap[8]=62 的大小关系，由千前者较小，继续交换 heap[3] 与 heap[8] ， 交 换后的 heap 如图 5.27 ( C) 图 所示，此时 p 指向叶结点 heap[8]， 针对 heap[1] 的调整过程结束。

---

---

（三）算法代码

void AdjustDown(ElemType heap[], int current, int border)
{
	int p = current;
	int minChild;
	ElemType temp;
	// p 不是叶子结点	 说明 p 结点 有左孩子 或者 有左孩子且有右孩子
	while (2 * p + 1 <= border)
	{
		// 如果右孩子存在 且 左孩子大于右孩子
		if ((2 * p + 2 <= border) && heap[2 * p + 1] > heap[2 * p + 2])
		{
			minChild = 2 * p + 2;
		}
		else  // 不存在右孩子 或 左孩子小于右孩子
		{
			minChild = 2 * p + 1;
		}
		if (heap[p] <= heap[minChild])
			break;
		else
		{
			temp = heap[p];
			heap[p] = heap[minChild];
			heap[minChild] = temp;
			p = minChild;
		}
	}
}

void CreateHeap(ElemType heap[], int n)
{
	int i;
	for (i = (n - 2) / 2; i > -1; i--)
	{
		AdjustDown(heap, i, n - 1);
	}
}

（四）算法代码实例

设有初始序列 { 61 , 28 , 81 , 43 , 36 , 47 , 83 , 5 } \{6 1, 28, 81, 43 , 36 , 47, 83, 5 \} {61,28,81,43,36,47,83,5}针对该序列的建堆运算的执行过程，其具体过程如下表所示：

（五）AdjustDown算法复杂度分析

下面， 我们分析该算法的时间复杂度。AdjustDown 函数的调用过程是从位千 $\lfloor n-2)/2\rfloor$ 处的元素开始的 ，直到完成堆顶元索的向下调整为止。每执行一次 AdjustDown 函数的时间复杂度是 $O(lo{g}_{2}n)$ ，因此直观上，建堆的时间复杂度为 $O(lo{g}_{2}n)$ 。然而实际上，建堆的时间复杂度为 $O(n)$，此处不作详细分析 。

三、全部代码

#include 
#define ElemType int

#define N 8

void AdjustDown(ElemType heap[], int current, int border)
{
	int p = current;
	int minChild;
	ElemType temp;
	// p 不是叶子结点	 说明 p 结点 有左孩子 或者 有左孩子且有右孩子
	while (2 * p + 1 <= border)
	{
		// 如果右孩子存在 且 左孩子大于右孩子
		if ((2 * p + 2 <= border) && heap[2 * p + 1] > heap[2 * p + 2])
		{
			minChild = 2 * p + 2;
		}
		else  // 不存在右孩子 或 左孩子小于右孩子
		{
			minChild = 2 * p + 1;
		}
		if (heap[p] <= heap[minChild])
			break;
		else
		{
			// 交换变量的值
			temp = heap[p];
			heap[p] = heap[minChild];
			heap[minChild] = temp;
			p = minChild;
		}
	}
}

void CreateHeap(ElemType heap[], int n)
{
	int i;
	for (i = (n - 2) / 2; i > -1; i--)
	{
		AdjustDown(heap, i, n - 1);
	}
}


// 打印堆
void PrintHeap(ElemType heap[], int n)
{
	for (int i = 0 ; i <n; i++)
	{
		printf("%d ", heap[i]);
	}
}

int main()
{
	// 原始无序序列
	ElemType heap[N] = { 61, 28, 81, 43, 36, 47, 83, 5 };

	// 建堆
	CreateHeap(heap, 8);

	// 打印建好的堆
	PrintHeap(heap, 8);

	return 0;
}