【NeurIPS && 图谱问答】知识图谱(KG) Mutil-Hop推理的锥形嵌入方法（中科院--含源码）

来源: AINLPer 微信公众号（每日论文干货分享！！）
编辑: ShuYini
校稿: ShuYini
时间: 2022-09-29

引言

知识图谱（Knowledge Graph）是以三元组形式，将数据存储在图数据库中。实现知识图谱问答，核心是将自然语言转化为在图数据的查询语言，也就是将自然语言问题映射到结构化查询的过程。当KGs中缺少一些环节时，它很难识别正确的答案，如果解决这个问题，本篇文章或许能够帮到你。论文及源码连接在后面

背景介绍

 基于知识图谱（KGs）的Multi-Hop推理，旨在使用来自 KGs 的知识找到给定查询的答案实体，近年来受到了学术界和产业界的广泛关注。一般来说，它涉及使用运算符(包括存在量化(∃)、合(∧)、分离(∨)和否定(¬)来回答关于KGs的一阶逻辑(FOL)查询。在KGs上进行Multi-Hop推理的一种常用方法是：首先将一个FOL查询转换为相应的计算图(其中每个节点表示一组实体，每个边表示一个逻辑操作)，然后根据计算图遍历KG以识别答案集。然而，这种方法面临两大挑战。首先，当KGs中缺少一些环节时，它很难识别正确的答案。其次，它需要处理推理路径上的所有中间实体，这可能导致计算成本呈指数级。

 为了解决这些问题，研究人员越来越重视查询嵌入(QE)技术，它将实体和FOL查询嵌入到低维空间中。量化宽松模型将计算图中的每个逻辑运算符与嵌入空间中的一个逻辑运算符关联起来。给定一个查询，QE模型根据相应的计算图生成查询嵌入。然后，它们根据查询嵌入和实体嵌入之间的相似性来确定一个实体是否是正确答案。

 在现有的QE模型中，基于几何模型将实体和查询嵌入到几何形状中表现出了良好的性能。基于几何模型通常将实体集表示为欧氏空间中的“区域”(例如，点和框)，然后在它们上进行集合操作。例如，Query2Box将实体表示为点，将查询表示为框。如果一个点在一个框内，那么对应的实体就是查询的答案。与非几何方法相比，几何形状提供了一种自然的、易于解释的表示集合及其逻辑关系的方法。

 然而，现有的基于几何的模型很难对带有否定的查询进行建模，这大大限制了其适用性。例如，GQE和Query2Box——别将查询嵌入到点和框中——不能处理带有否定的查询，因为点/框的补码不再是点/框。为了解决这个问题，Ren & Leskovec 提出了一个使用Beta分布的概率量化宽松模型。但是，它不具备几何模型的一些优点。例如，在使用Beta分布时，不清楚如何确定一个实体是否为box case 中的查询的答案。因此，提出一个能够模拟所有FOL查询的几何QE模型仍然具有挑战性。

Cone模型介绍

 本文提出了一种新的查询嵌入模型，即锥嵌入(Cone Embeddings)，用于回答知识图上的Mutil-Hop一阶逻辑(FOL)查询。我们将实体集表示为锥的笛卡尔积，并设计相应的逻辑运算。

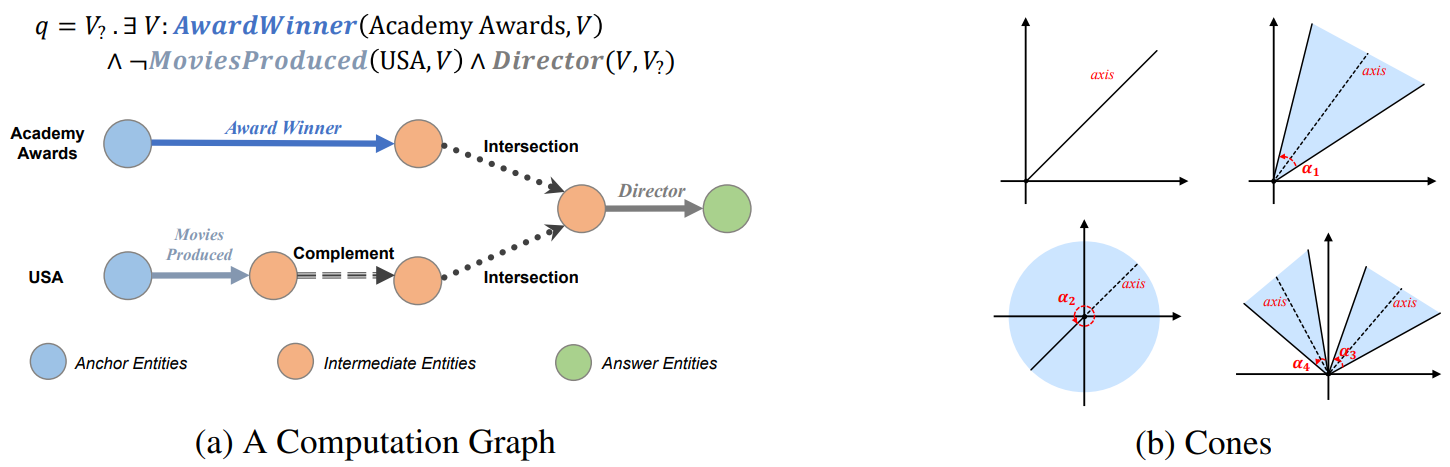
Cone Embeddings

 给定一个查询，我们将推理过程表示为一个计算图(上图a)，其中节点表示实体集，边表示实体集上的逻辑操作。上图b给出了几个(扇形)锥的例子，可能会注意到扇区锥与Query2Box中定义的框有一些相似之处，后者也涉及到区域表示。然而，相比之下，扇形锥比方框更有表现力。

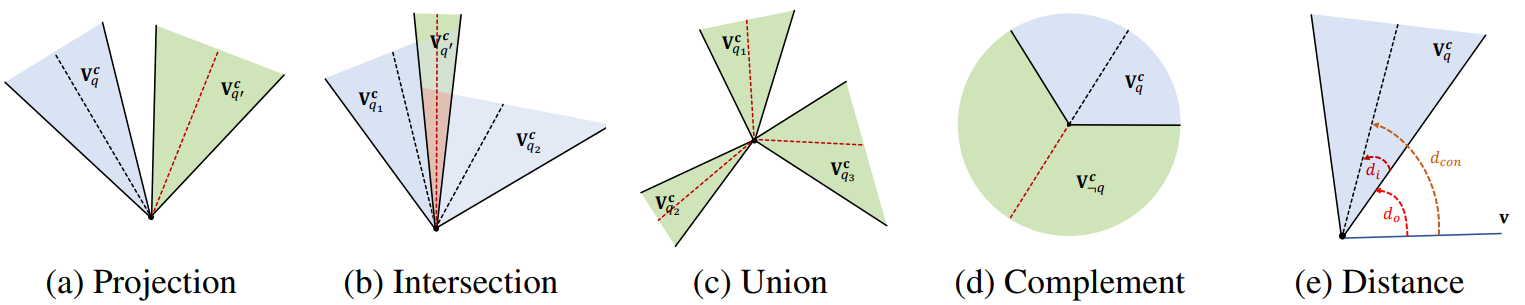
Cone Logical operation

Projection Operator P：如上图a所示，P的目标是表示一个实体的相邻实体，这些实体由给定的关系连接起来。它将一个实体集映射到另一个实体集。

Intersection Operator L：如上图b所示，给定一个请求q，它的连接请求实体集是$[q_1]、[q_2]$的交集，那么操作L的目的是：$[q]= {\textstyle \bigcap_{i=1}^{n}} [q_i] $

Union Operator U：如上图c所示，给定一个请求q，且它的连接查询请求实体集$[q_1]、[q_2]、[q_3]$是分开的，那么操作U的目的是：将这些分散集合统一到一起，即：$[q]={\bigcup }_{i=1}^n[q_i]$

Complement Operator C：如上图d所示，给定一个连接查询请求q以及其对应的实体集[q]，操作C的目的是能够识别[¬q]为请求q的补集。

Distance Functio：为连接查询定义距离函数。受Ren等的启发，我们将距离d分为两部分——外部距离$d_o$和内部距离$d_i$。上图e给出了距离函数d的说明。

实验快照

 在本节中，我们通过实验证明:1)ConE是一个强大的知识图Mutil-hop推理模型;2) ConE的锥形嵌入能有效地模拟答案集的基数(即元素个数)。

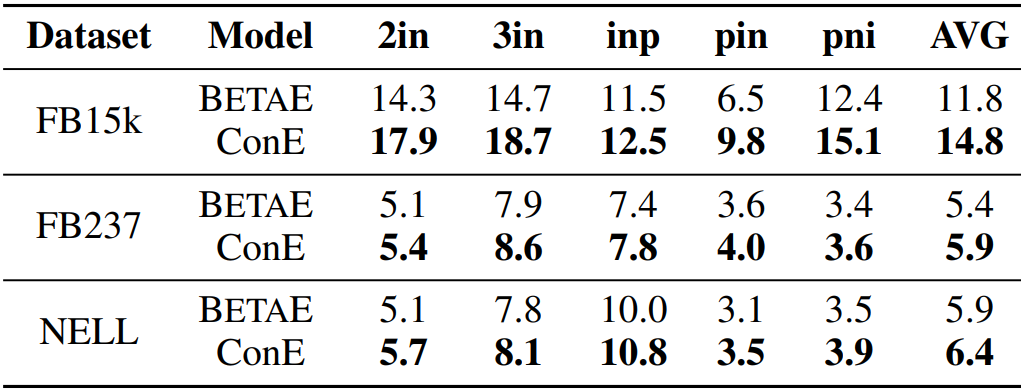
 1、下表显示了在没有否定的查询上的实验结果，即存在正一阶(EPFO)查询，其中AVG表示平均性能。总体而言，ConE的表现明显优于比较模型。

 2、下表显示了ConE与BETAE在建模带有否定的FOL查询时的结果。由于GQE和Q2B不具备处理否定算符的能力，我们不将他们的结果纳入实验。总体而言，ConE的表现大大优于BETAE

推荐阅读

[1] 必看！！【AINLPer】自然语言处理（NLP）领域知识&&资料大分享

[2]【历年NeurIPS论文下载】一文带你看懂NeurIPS国际顶会（内含NeurIPS2022）

[3]【NLP论文分享&&语言表示】有望颠覆Transformer的图循环神经网络（GNN）

[4]【NeurIPS && 图谱问答】知识图谱(KG) Mutil-Hop推理的锥形嵌入方法（中科院–含源码）

[5]【NLP论文分享 && QA问答】动态关联GNN建立直接关联，优化multi-hop推理（含源码）

[6]【历年IJCAI论文下载 && 论文速递】无数据对抗蒸馏、垂直联合、预训练微调范式图神经网络（GNN）

[7]【NLP论文分享 && 含源码】基于Prompting Seq2Seq的自动标签序列生成（清华AI研究院）

[8]【NLP论文分享&&PLM源码】预训练模型BERT玩转Twitter(70亿数据对、100多种语言)

[9]【论文速递 && IJCAI论文干货下载】图神经网络(GNN)(多行为推荐、多模态食谱表示学习、同质图表示学习)

[10]【历年IJCAI论文下载 && 论文速递】无数据对抗蒸馏、垂直联合、预训练微调范式图神经网络（GNN）

[11]【NLP论文分享&&中文命名实体识别】如何构建一个优秀的Gazetteer/地名词典（浙大&含源码）

[12]一文看懂线性回归【比较详细】(内含源码)

[13]一文看懂逻辑回归【比较详细】(含源码)

论文&&源码

Title: ConE: Cone Embeddings for Multi-Hop Reasoning over Knowledge Graphs
Author: 中国科学院全球科学院技术重点实验室
Paper：https://arxiv.org/pdf/2110.13715.pdf
Code：https://github.com/MIRALab-USTC/QE-ConE.

最后不是最后

关注 AINLPer 微信公众号（每日都有最新的论文推荐给你！！）