单调栈的本质与应用

单调栈的本质与应用
单调栈的定义与证明

前言

　　最近领悟到了单调栈的本质，特此来记录一下我的理解。

　　单调栈主要用来解决这样一类问题，当枚举到下标$i$，要求在下标$i$之前小于$/$大于$val$的数的下标中，找到最小$/$最大的下标位置。

　　一共有四种不同的情况，下面来证明在这四种情况中，栈内维护的元素始终单调递增或单调递减的。

在小于$val$的数中找到最小下标

　　当我们枚举到下标$i$，同时给定一个数$val$，现在我们要在下标$i$之前的数中找到满足数值小于$val$的数的下标，然后在这些满足条件的数的下标中找到最小的下标。

　　很容易想到的一个做法是从前面开始暴力枚举每一个数，如果找到第一个小于$val$的数，那么就返回这个数的下标，这个下标一定是最小的下标。一共有$n$次询问，而每次询问都要用$O(n)$的计算量去找到最小的下标，因此暴力做法的时间复杂度是$O(n^2)$，这个时间复杂度就太高了，我们需要对它进行优化。

　　我们用一个栈去模拟上面暴力枚举的过程。一开始栈为空，每当$i$往右走，就往栈压入一个元素（这里压入的是下标），因此当枚举到$i$时，栈里存储的是下标$1 \sim i-1$（下标从$1$开始），每次要找最小下标时都是从栈底开始找（即栈里存下标$1$的位置开始找），直到找到第一个比$val$小的下标所对应的数为止。既然可以对这个过程进行优化，那么意味着存在冗余，我们看一下栈里是否存在某些元素永远也不会作为答案输出来。

　　假设有位置$x < y$，同时下标所对应的数$a_x \leq a_y$，那么$a_y$就没有存在的必要了。这是因为如果$a_y < val$，那么就一定有$a_x < val$，而$a_x$所对应的下标小于$a_y$所对应的下标，即$x < y$，因此肯定要选$x$而不是$y$。

　　因此结论就是如果前一个数要比后一个数小（相等）的话，那么后一个数就没有存在的必要了。

　　因此对于某个位置$j~(j < i)$，把$j+1 \sim i-1$这些位置上大于$a_j$的下标删去，最后整个栈的元素就是单调递减的，如图：

　　现在我们要在这个序列中找到小于$val$的最小的下标，由于满足单调性就可以用二分来做。

　　然后现在要把下标$i$压入栈中，由于此时刚遍历完$i$，在栈中$i$后面没有数，因此不用考虑后面是否有比这个$i$位置上大的数。而要考虑$i$前面的下标，只有当$a_i$小于栈顶元素所对应的数$a[stk[tp]]$时，才能将下标$i$压入栈，这是因为前面的数要比后面的数小，否则后面的数要被删除。如果每次都根据这个规则来将元素压入栈这样就能保证栈中元素是单调递减的了。

在小于$val$的数中找到最大下标

　　当我们枚举到下标$i$，同时给定一个数$val$，现在我们要在下标$i$之前的数中找到满足数值小于$val$的数的下标，然后在这些满足条件的数的下标中找到最大的下标。

　　假设有位置$x < y$，同时下标所对应的数$a_x \geq a_y$，那么$a_x$就没有存在的必要了。这是因为如果$a_x < val$，那么就一定有$a_y < val$，而$a_y$所对应的下标大于$a_x$所对应的下标，即$y > x$，因此肯定要选$y$而不是$x$。

　　因此结论就是如果前一个数要比后一个数大（相等）的话，那么前一个数就没有存在的必要了。

　　因此对于某个位置$j~(j < i)$，把下标$j$之前的位置上大于$a_j$的下标删去，最后整个栈的元素就是单调递增的，如图：

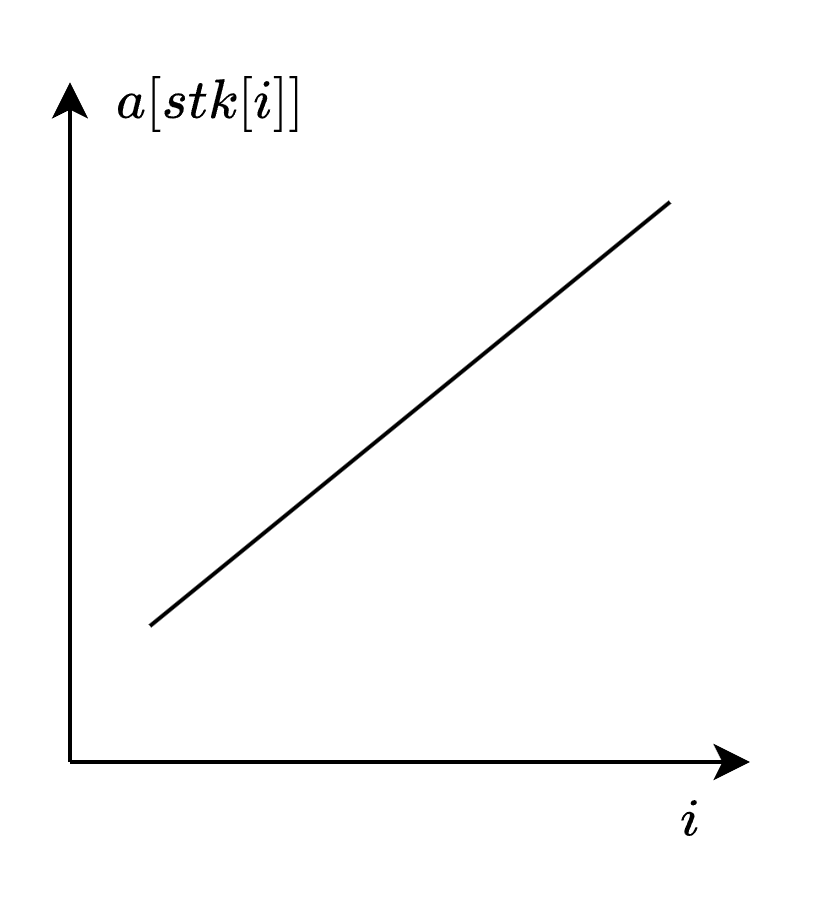
　　现在我们一样用上面的方法，即通过二分来找到这个序列中小于$val$的最大的下标，这样做肯定是正确的。

　　然后现在要把下标$i$压入栈中，此时$i$后面没有数且这种情况只考虑前面位置的数，那么我们只需要看栈中存放的下标就可以了。由于栈中存放的下标都是小于$i$的，并且根据前面结论如果前一个数要比后一个数大（相等）的话，那么就把前一个数删掉，因此我们每次弹出栈顶元素，比较$a[stk[tp]]$与$a[i]$的大小，如果发现$a[stk[tp]] \geq a[i]$，那么那么就应该把栈顶元素删除，重复这个过程直到栈为空（意味着前面所有元素都比$a[i]$大或相等）或者有$a[stk[tp]] < a[i]$（前面剩下的元素都是小于$a[i]$的）。这样将元素压入栈就能保证栈中元素是单调递增的了。

　　可以发现，上面将$i$压入栈的过程就已经找到了比$a[i]$小的数的最大下标了，因此就没必要再用二分了。

在大于$val$的数中找到最小下标

　　当我们枚举到下标$i$，同时给定一个数$val$，现在我们要在第$i$个下标之前的数中找到满足数值大于$val$的数的下标，然后在这些满足条件的数的下标中找到最小的下标。

　　假设有位置$x < y$，同时下标位置上的数$a_x \geq a_y$，那么$a_y$就没有存在的必要了。这是因为如果$a_y > val$，那么就一定有$a_x > val$，而$a_x$所对应的下标小于$a_y$所对应的下标，即$x < y$，因此肯定要选$x$而不是$y$。

　　因此结论就是如果前一个数要比后一个数大（相等）的话，那么后一个数就没有存在的必要了。

　　因此对于某个位置$j~(j < i)$，把$j+1 \sim i-1$这些位置上小于$a_j$的下标删去，最后整个栈的元素就是单调递增的，如图：

　　现在我们要在这个序列中找到大于$val$的最小的下标，由于满足单调性就可以用二分来做。

　　然后现在要把下标$i$压入栈中，由于此时刚遍历完$i$，栈中的$i$后面没有数，因此不用考虑后面是否有比这个$i$位置上小的数。而要考虑$i$前面的下标，只有当$a_i$大于栈顶元素所对应的数$a[stk[tp]]$时，才能将下标$i$压入栈，这是因为前面的数要比后面的数小，否则后面的数要被删除。如果每次都根据这个规则来将元素压入栈这样就能保证栈中元素是单调递增的了。

在大于$val$的数中找到最大下标

　　当我们枚举到下标$i$，同时给定一个数$val$，现在我们要在第$i$个下标之前的数中找到满足数值大于$val$的数的下标，然后在这些满足条件的数的下标中找到最大的下标。

　　假设有位置$x < y$，同时下标位置上的数$a_x \leq a_y$，那么$a_x$就没有存在的必要了。这是因为如果$a_x > val$，那么就一定有$a_y > val$，而$a_y$所对应的下标大于$a_x$所对应的下标，即$y > x$，因此肯定要选$y$而不是$x$。

　　因此结论就是如果前一个数要比后一个数小（相等）的话，那么前一个数就没有存在的必要了。

　　因此对于某个位置$j~(j < i)$，把下标$j$之前的位置上小于$a_j$的下标删去，最后整个栈的元素就是单调递减的，如图：

　　先考虑把下标$i$压入栈，此时$i$后面没有数且这种情况只考虑前面的数，那么我们只需要看栈中存放的下标就可以了。由于栈中存放的下标都是小于$i$的，并且根据前面结论如果前一个数要比后一个数小（相等）的话，那么就把前一个数删掉，因此我们每次弹出栈顶元素，比较$a[stk[tp]]$与$a[i]$的大小，如果发现$a[stk[tp]] \leq a[i]$，那么那么就应该把栈顶元素删除，重复这个过程直到栈为空（意味着前面所有元素都比$a[i]$小或相等）或者有$a[stk[tp]] > a[i]$（前面剩下的元素都是大于$a[i]$的）。这样将元素压入栈就能保证栈中元素是单调递增的了，同时这个过程也找到栈中比$a[i]$大的数的最大下标，不需要二分。

总结
1. 要在小于$val$的数中找到最小下标，这种情况的栈是单调递减的，找到最小下标需要用到二分，只有当前下标所对应的数小于栈顶元素所对应的数时才可以压入栈。
2. 要在小于$val$的数中找到最大下标，这种情况的栈是单调递增的，找到最大下标不需要用到二分，持续弹出栈顶元素直到栈顶元素所对应的数小于当前下标所对应的数，此时栈顶元素就是最大下标，同时把当前下标压入栈。
3. 要在大于$val$的数中找到最小下标，这种情况的栈是单调递增的，找到最小下标需要用到二分，只有当前下标所对应的数大于栈顶元素所对应的数时才可以压入栈。
4. 要在大于$val$的数中找到最大下标，这种情况的栈是单调递减的，找到最大下标不需要用到二分，持续弹出栈顶元素直到栈顶元素所对应的数大于当前下标所对应的数，此时栈顶元素就是最大下标，同时把当前下标压入栈。
　　现在来看的话理解单调栈这个模型并没有太大的困难，关键是在做题的时候要抽象出这个模型，这样才可以用上面的方法来解题。

　　下面来举例几个用到单调栈的题目，都需要将这个模型抽象出来。

单调栈

给定一个长度为 $N$ 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 $−1$。

输入格式

第一行包含整数 $N$，表示数列长度。

第二行包含 $N$ 个整数，表示整数数列。

输出格式

共一行，包含 $N$ 个整数，其中第 $i$ 个数表示第 $i$ 个数的左边第一个比它小的数，如果不存在则输出 $−1$。

数据范围

$1 \leq N \leq {10}^{5}$
$1 \leq \text{数列中元素} \leq {10}^{9}$

输入样例：
```
5
3 4 2 7 5
```
输出样例：
```
-1 3 -1 2 2
```
解题思路

　　题目要求对于每个位置上的数找到左边第一个比它小的数，也就是说对于下标$i$位置上的数$a_i$，要在下标$i$之前找到所有小于$a_i$的数中下标最大的那个。这个就是我们上面说到的在小于$val$的数中找到最大下标这个模型。现在已经把模型抽象出来了，下面就可以用代码实现了。

　　AC代码如下，时间复杂度为$O(n)$：
```
 1 #include 
 2 using namespace std;
 3 
 4 const int N = 1e5 + 10;
 5 
 6 int a[N];
 7 int stk[N], tp;
 8 
 9 int main() {
10     int n;
11     scanf("%d", &n);
12     for (int i = 1; i <= n; i++) {
13         scanf("%d", a + i);
14     }
15     
16     for (int i = 1; i <= n; i++) {
17         while (tp && a[stk[tp]] >= a[i]) {  // 把>=a[i]的栈顶元素全部弹出
18             tp--;
19         }
20         if (tp) printf("%d ", a[stk[tp]]);  // 此时栈顶元素就是最大下标
21         else printf("-1 "); // 栈为空表示i前面不存在小于a[i]的数
22         stk[++tp] = i;  // 此时栈顶元素必然小于a[i]，把i压入栈中
23     }
24     
25     return 0;
26 }
```
　　以下内容是线段树以及树状数组的解法，可以略过。

　　顺便扩展一下，这题还可以用线段树来做。用到的是值域线段树，即线段树维护的是值域$a_i$的若干个区间，而不是下标区间。每次询问都是要找小于$a_i$的最大下标，因此可以用线段树来维护每个数值所对应的最大下标，即每次查询都问某个前缀区间的最大值。由于数值的取值范围很大，因此需要进行离散化。

　　AC代码如下，时间复杂度为$O(n \log{n})$：
```
 1 #include 
 2 using namespace std;
 3 
 4 const int N = 1e5 + 10;
 5 
 6 int a[N];
 7 int xs[N], sz;
 8 struct Node {
 9     int l, r, maxv;
10 }tr[N * 4];
11 
12 void build(int u, int l, int r) {
13     if (l == r) {
14         tr[u] = {l, r};
15     }
16     else {
17         int mid = l + r >> 1;
18         build(u << 1, l, mid);
19         build(u << 1 | 1, mid + 1, r);
20         tr[u] = {l, r};
21     }
22 }
23 
24 void modify(int u, int x, int c) {
25     if (tr[u].l == x && tr[u].r == x) {
26         tr[u].maxv = max(tr[u].maxv, c);
27     }
28     else {
29         if (x <= tr[u].l + tr[u].r >> 1) modify(u << 1, x, c);
30         else modify(u << 1 | 1, x, c);
31         tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
32     }
33 }
34 
35 int query(int u, int l, int r) {
36     if (tr[u].l >= l && tr[u].r <= r) return tr[u].maxv;
37     int mid = tr[u].l + tr[u].r >> 1, ret = 0;
38     if (l <= mid) ret = query(u << 1, l, r);
39     if (r >= mid + 1) ret = max(ret, query(u << 1 | 1, l, r));
40     return ret;
41 }
42 
43 int find(int x) {
44     int l = 1, r = sz;
45     while (l < r) {
46         int mid = l + r >> 1;
47         if (xs[mid] >= x) r = mid;
48         else l = mid + 1;
49     }
50     return l;
51 }
52 
53 int main() {
54     int n;
55     scanf("%d", &n);
56     for (int i = 1; i <= n; i++) {
57         scanf("%d", a + i);
58         xs[++sz] = a[i];
59     }
60 
61     sort(xs + 1, xs + sz + 1);
62     sz = unique(xs + 1, xs + sz + 1) - xs - 1;
63 
64     build(1, 1, sz);
65 
66     for (int i = 1; i <= n; i++) {
67         int t = query(1, 1, find(a[i]) - 1);    // 如果是qurty(1, 1, 0)那么会返回0
68         modify(1, find(a[i]), i);
69         printf("%d ", t ? a[t] : -1);
70     }
71 
72     return 0;
73 }
```
　　这里有个小技巧，就是由于询问的是$< a_{i}$的数，即询问$\leq a_{i}-1$的数，由于我们会用到$a_{i}-1$，因此应该把$a_{i}-1$也进行离散化的，但可以发现上面的代码并没有这么做。其实可以发现本质上是找$a_{i}$的前一个数，即便我们把$a_{i}-1$进行离散化，也不会对$a_{i}-1$进行任何修改操作，于是可以不对$a_{i}-1$进行离散化，而直接把$a_{i}$离散化后的前一个位置作为前一个数。这种做法可以降低一下常数，防止被卡。

　　可以发现由于每次询问的区间都是以开始$1$开始的前缀的最大值，因此这里还可以用树状数组来实现，AC代码如下，时间复杂度为$O(n \log{n})$：
```
 1 #include 
 2 using namespace std;
 3 
 4 const int N = 1e5 + 10;
 5 
 6 int a[N];
 7 int xs[N], sz;
 8 int tr[N];
 9 
10 int lowbit(int x) {
11     return x & -x;
12 }
13 
14 void add(int x, int c) {
15     for (int i = x; i <= sz; i += lowbit(i)) {
16         tr[i] = max(tr[i], c);
17     }
18 }
19 
20 int query(int x) {
21     int ret = 0;
22     for (int i = x; i; i -= lowbit(i)) {
23         ret = max(ret, tr[i]);
24     }
25     return ret;
26 }
27 
28 int find(int x) {
29     int l = 1, r = sz;
30     while (l < r) {
31         int mid = l + r >> 1;
32         if (xs[mid] >= x) r = mid;
33         else l = mid + 1;
34     }
35     return l;
36 }
37 
38 int main() {
39     int n;
40     scanf("%d", &n);
41     for (int i = 1; i <= n; i++) {
42         scanf("%d", a + i);
43         xs[++sz] = a[i];
44     }
45     
46     sort(xs + 1, xs + sz + 1);
47     sz = unique(xs + 1, xs + sz + 1) - xs - 1;
48     
49     for (int i = 1; i <= n; i++) {
50         int t = query(find(a[i]) - 1);  // 如果是query(0)那么会返回0
51         printf("%d ", t ? a[t] : -1);
52         add(find(a[i]), i);
53     }
54     
55     return 0;
56 }
```
　　其实上面说到的$4$个模式都是可以用线段树和树状数组实现的，但还是不建议这么做，一方面是代码很难写，另一方面是常数比较大，同样是$O(n \log{n})$的复杂度，单调栈的做法就不会被卡，而线段树或树状数组就很容易被卡常数。

最长连续子序列

给定一个长度为 $n$ 的整数序列 $a_1,a_2, \dots ,a_n$。

现在，请你找到一个序列 $a$ 的连续子序列 $a_{l},a_{l+1}, \dots ,a_{r}$，要求：
- ${\sum\limits_{i=l}^{r}{a_i}} > 100 \times (r - l + 1)$。
- 连续子序列的长度（即 $r−l+1$）尽可能大。
请你输出满足条件的连续子序列的最大可能长度。

输入格式

第一行包含整数 $n$。

第二行包含 $n$ 个整数 $a_1,a_2, \dots ,a_n$。

输出格式

一个整数，表示最大可能长度。

如果满足条件的连续子序列不存在，则输出 $0$。

数据范围

前三个测试点满足 $1 \leq n \leq 5$。
所有测试点满足 $1 \leq n \leq {10}^{6}$，$0 \leq a_i \leq 5000$。

输入样例1：
```
1 5
2 100 200 1 1 1
```
输出样例1：
```
3
```
输入样例2：
```
5
1 2 3 4 5
```
输出样例2：
```
0
```
输入样例3：
```
2
101 99
```
输出样例3：
```
1
```
解题思路

　　我们把式子做一下等价变换，得到$$\frac{\sum\limits_{i=l}^{r}{a_i}}{r - l + 1} > 100$$可以发现就是区间$l \sim r$的平均数要满足大于$100$，等价于我们对这个区间的每一个数都减去$100$，最后算得的平均数要大于$0$，证明如下，$$\begin{align*} \frac{\sum\limits_{i=l}^{r}{a_i}}{r - l + 1} &> 100 \\ \frac{\sum\limits_{i=l}^{r}{a_i}}{r - l + 1} - 100 &> 0 \\ \frac{\sum\limits_{i=l}^{r}{a_i - {100 \times (r - l + 1)}}}{r - l + 1} &> 0 \\ \frac{\sum\limits_{i=l}^{r}{(a_i - 100)}}{r - l + 1} &> 0 \end{align*}$$

　　我们定义$b_i = a_i - 100$，同时用前缀和的思想，定义$s_i = \sum\limits_{j=1}^{i}{b_j}$，再把式子进行变换，得到$$\frac{s_{r} - s_{l-1}}{r - l + 1} > 0$$

　　现在我们要求满足上式的条件的一个长度最大的区间$l \sim r$，由于$r-l+1 > 0$ 因此可以直接约去分母，上式就变成$s_{r} - s_{l-1} > 0$，即$s_{l'} < s_{r}$（定义${l'} = l-1$，$0 \leq {l'} \leq r-1$），问题就变成了当我们固定了右端点$r$后，要在$r$的左边找到一个满足$s_{l'} < s_{r}$，同时为最小的$l'$。

　　这个就是我们上面说到的在小于$val$的数中找到最小下标这个模型。

　　AC代码如下，时间复杂度为$O(n \log{n})$：
```
 1 #include 
 2 using namespace std;
 3 
 4 typedef long long LL;
 5 
 6 const int N = 1e6 + 10;
 7 
 8 LL s[N];
 9 int stk[N], tp;
10 
11 int main() {
12     int n;
13     scanf("%d", &n);
14     for (int i = 1; i <= n; i++) {
15         scanf("%d", s + i);
16         s[i] += s[i - 1] - 100; // 求b[i]的前缀和，b[i] = a[i] - 100
17     }
18     
19     int ret = 0;
20     for (int i = 1; i <= n; i++) {
21         // 当枚举到i，要把前一个元素即i-1压入栈
22         // 只有栈为空（初始状态）或s[i-1]小于栈顶元素所对应的数s[stk[tp]]时才能压入栈
23         if (!tp || s[i - 1] < s[stk[tp]]) stk[++tp] = i - 1;
24         
25         // 二分，由于栈内元素式单调递减的，因此要在下标[0, i-1]中找到小于s[i]最左边的那个数，对应的是最小下标
26         int l = 1, r = tp;
27         while (l < r) {
28             int mid = l + r >> 1;
29             if (s[stk[mid]] < s[i]) r = mid;
30             else l = mid + 1;
31         }
32         
33         if (s[stk[l]] < s[i]) ret = max(ret, i - stk[l]);   // 找到才可以作为一个合法的答案
34     }
35     
36     printf("%d", ret);
37     
38     return 0;
39 }
```
　　同时给出树状数组实现的代码，由于这题卡常数，因此线段树的代码会TLE，树状数组的时间开销也比较极限。

　　AC代码如下，时间复杂度为$O(n \log{n})$：
#include using namespace std; typedef long long LL; const int N = 1e6 + 10; LL s[N]; LL xs[N], sz; int tr[N]; int find(LL x) { int l = 1, r = sz; while (l < r) { int mid = l + r >> 1; if (xs[mid] >= x) r = mid; else l = mid + 1; } return l; } int lowbit(int x) { return x & -x; } void add(int x, int c) { for (int i = x; i <= sz; i += lowbit(i)) { tr[i] = min(tr[i], c); } } int query(int x) { int ret = N; for (int i = x; i; i -= lowbit(i)) { ret = min(ret, tr[i]); } return ret; } int main() { int n; scanf("%d", &n); for (int i = 1; i <= n; i++) { scanf("%d", s + i); s[i] += s[i - 1] - 100; xs[++sz] = s[i]; } xs[++sz] = 0; sort(xs + 1, xs + sz + 1); sz = unique(xs + 1, xs + sz + 1) - xs - 1; memset(tr, 0x3f, sizeof(tr)); int ret = 0; for (int i = 1; i <= n; i++) { add(find(s[i - 1]), i - 1); ret = max(ret, i - query(find(s[i]) - 1)); } printf("%d", ret); return 0; }
树状数组
　　补充我当时想到的思路，当时没想到平均数这些东西，直接对式子做等价变换，得到$s_{l-1} - 100 \cdot (l + 1) < s_{r} - 100 \cdot r$，这里的$s_i$是对$a_i$的前缀和。然后定义$f(i) = s_{i} - 100 \cdot i$，于是式子就变成了$f(l-1)
　　AC代码如下，时间复杂度为$O(n \log{n})$：
#include using namespace std; typedef long long LL; const int N = 1e6 + 10; LL s[N]; LL xs[N], sz; int tr[N]; LL f(int x) { return s[x] - 100 * x; } int find(LL x) { int l = 1, r = sz; while (l < r) { int mid = l + r >> 1; if (xs[mid] >= x) r = mid; else l = mid + 1; } return l; } int lowbit(int x) { return x & -x; } void add(int x, int c) { for (int i = x; i <= sz; i += lowbit(i)) { tr[i] = min(tr[i], c); } } int query(int x) { int ret = N; for (int i = x; i; i -= lowbit(i)) { ret = min(ret, tr[i]); } return ret; } int main() { int n; scanf("%d", &n); for (int i = 1; i <= n; i++) { scanf("%d", s + i); s[i] += s[i - 1]; xs[++sz] = f(i); } xs[++sz] = 0; sort(xs + 1, xs + sz + 1); sz = unique(xs + 1, xs + sz + 1) - xs - 1; memset(tr, 0x3f, sizeof(tr)); int ret = 0; for (int i = 1; i <= n; i++) { add(find(f(i - 1)), i - 1); ret = max(ret, i - query(find(f(i)) - 1)); } printf("%d", ret); return 0; }
树状数组-另外一种思路
销售出色区间

给你一份销售数量表 sales ，上面记录着某一位销售员每天成功推销的产品数目。

我们认为当销售员同一天推销的产品数目大于 $8$ 个的时候，那么这一天就是「成功销售的一天」。

所谓「销售出色区间」，意味在这段时间内，「成功销售的天数」是严格大于「未成功销售的天数」。

请你返回「销售出色区间」的最大长度。

示例 1：
```
输入：sales = [10,2,1,4,3,9,6,9,9]
输出：5
解释：最大销售出色区间是 [3,9,6,9,9]。
```
示例 2：
```
输入：sales = [5,6,7]
输出：0
```
提示：

$1 \leq sales.length \leq {10}^{4}$
$0 \leq sales[i] \leq 16$

解题思路

　　求一个连续区间的某个数目，应该想到试一下能不能用前缀和。先扫描一遍$sales$数组，同时定义一个数组$s$，如果$sales[i] > 8$，就把$s[i]$置为$1$，否则就置为$-1$，再对$s$数组求前缀和，那么问题就变成了我们要在$s$数组中找到一个最长的区间$[l,r]$，满足$s_{r} - s_{l-1} > 0$，即$s_{l-1} < s_{r}$，这就变得和上一题一样，当固定了右端点$r$后，要在$r$的左边找到一个满足$s_{l-1} < s_{r}$，同时为最小的$l-1$。同样是在小于$val$的数中找到最小下标这个模型。

　　AC代码如下，时间复杂度为$O(n \log{n})$：
```
 1 class Solution {
 2 public:
 3     int longestESR(vector<int>& sales) {
 4         int n = sales.size();
 5         vector<int> s(n + 1);
 6         for (int i = 1; i <= n; i++) {
 7             s[i] += s[i - 1] + (sales[i - 1] > 8 ? 1 : -1);
 8         }
 9         
10         int ret = 0;
11         vector<int> stk;
12         for (int i = 1; i <= n; i++) {
13             if (stk.empty() || s[i - 1] < s[stk.back()]) stk.push_back(i - 1);
14             int l = 0, r = stk.size() - 1;
15             while (l < r) {
16                 int mid = l + r >> 1;
17                 if (s[stk[mid]] < s[i]) r = mid;
18                 else l = mid + 1;
19             }
20             if (s[stk[l]] < s[i]) ret = max(ret, i - stk[l]);
21         }
22         
23         return ret;
24     }
25 };
```
　　线段树和树状数组实现的AC代码如下，时间复杂度均为$n \log{n}$：
const int N = 2e4 + 10; class Solution { public: struct Node { int l, r, minv; }tr[N * 4]; vector<int> s; void build(int u, int l, int r) { if (l == r) { tr[u] = {l, r, N}; } else { int mid = l + r >> 1; build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); tr[u] = {l, r, N}; } } void modify(int u, int x, int c) { if (tr[u].l == x && tr[u].r == x) { tr[u].minv = min(tr[u].minv, c); } else { if (x <= tr[u].l + tr[u].r >> 1) modify(u << 1, x, c); else modify(u << 1 | 1, x, c); tr[u].minv = min(tr[u << 1].minv, tr[u << 1 | 1].minv); } } int query(int u, int l, int r) { if (tr[u].l >= l && tr[u].r <= r) return tr[u].minv; int mid = tr[u].l + tr[u].r >> 1, ret = N; if (l <= mid) ret = query(u << 1, l, r); if (r >= mid + 1) ret = min(ret, query(u << 1 | 1, l, r)); return ret; } int longestESR(vector<int>& sales) { int n = sales.size(); s = vector<int>(n + 1); for (int i = 1; i <= n; i++) { s[i] += s[i - 1] + (sales[i - 1] > 8 ? 1 : -1); } build(1, -n - 1, n); // 值域是[-(n+1), n]，查询的时候s[i]还要减1 int ret = 0; for (int i = 1; i <= n; i++) { modify(1, s[i - 1], i - 1); ret = max(ret, i - query(1, -n - 1, s[i] - 1)); } return ret; } };
线段树
　　其中值域的范围是$[-n,n]$，对于树状数组需要将整个值域映射到正整数区间，因此可以对区间整体加上$n+1$，这样就可以映射到$[1, 2n+1]$了。
const int N = 2e4 + 10; class Solution { public: int n; int tr[N]; vector<int> s; int lowbit(int x) { return x &-x; } void add(int x, int c) { for (int i = x + n + 1; i <= n << 1; i += lowbit(i)) { tr[i] = min(tr[i], c); } } int query(int x) { int ret = N; for (int i = x + n + 1; i; i -= lowbit(i)) { ret = min(ret, tr[i]); } return ret; } int longestESR(vector<int>& sales) { n = sales.size(); s = vector<int>(n + 1); for (int i = 1; i <= n; i++) { s[i] += s[i - 1] + (sales[i - 1] > 8 ? 1 : -1); } memset(tr, 0x3f, sizeof(tr)); int ret = 0; for (int i = 1; i <= n; i++) { add(s[i - 1], i - 1); ret = max(ret, i - query(s[i] - 1)); } return ret; } };
树状数组
参考资料

　　AcWing 4487. 最长连续子序列（AcWing杯 - 周赛：https://www.acwing.com/video/4001/
相关阅读:
vue学习31~39（列表过滤+列表排序+vue检测data中的数据+收集表单数据+过滤器）
Ubuntu安装openssh-server出现失败
 先进制造aps专题四计划型简单aps系统(plan)和排产型复杂aps系统(Scheduling）的区别
 react中关于函数调用()与bind this的原因
 【数据结构】栈（C语言实现）
JAVA8新特性- 函数式接口
 Transformer模型 | Python实现基于LSTM与Transfomer的股票预测模型（pytorch）
搜索——最短路模型，多源bfs
Java架构师之路九、设计模式：常见的设计模式，如单例模式、工厂模式、策略模式、桥接模式等
 回归预测 | MATLAB实现带蒙特卡洛模拟的Bayes贝叶斯线性回归预测
原文地址：https://www.cnblogs.com/onlyblues/p/16736106.html

单调栈的定义与证明

前言

在小于$val$的数中找到最小下标

在小于$val$的数中找到最大下标

在大于$val$的数中找到最小下标

在大于$val$的数中找到最大下标

总结

单调栈

输入格式

输出格式

数据范围

输入样例：

输出样例：

解题思路

最长连续子序列

输入格式

输出格式

数据范围

输入样例1：

输出样例1：

输入样例2：

输出样例2：

输入样例3：

输出样例3：

解题思路

销售出色区间

示例 1：

示例 2：

提示：

解题思路

参考资料