【leetcode速通java版】02——有序数组、子数组、螺旋矩阵

前 言
🍉 作者简介：半旧518，长跑型选手，立志坚持写10年博客，专注于java后端
☕专栏简介：代码随想录leetcode速通训练营java版本
🌰 文章简介：leetcode-T977有序数组的平方 ,Leetcode-T209长度最小的子树组，Leetcode-T59螺旋矩阵二

leetcode-T977有序数组的平方

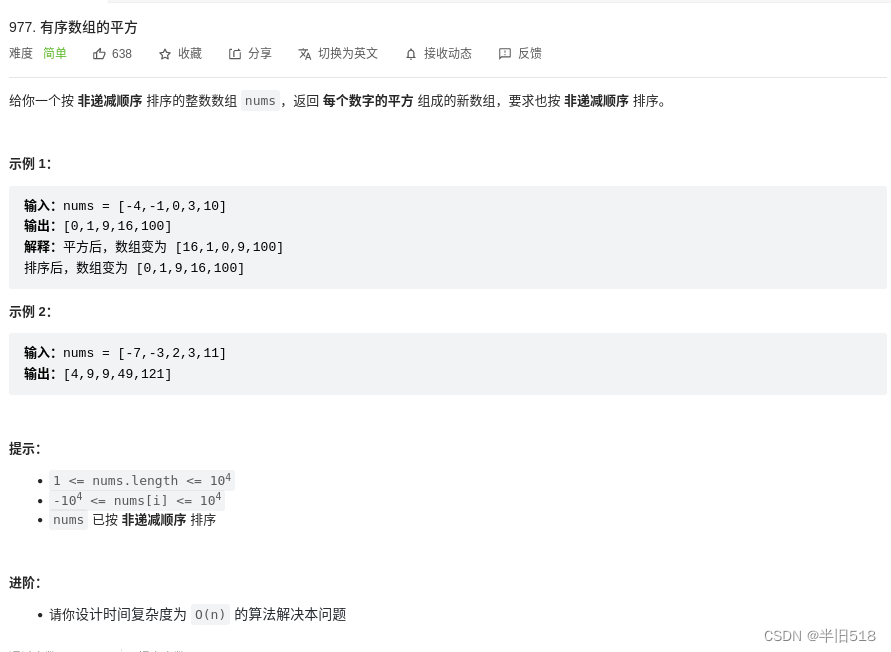
解法一：暴力破解法
先将数组中的元素遍历变成平方，再进行冒泡排序。

class Solution {
    public int[] sortedSquares(int[] nums) {
            for(int i = 0; i < nums.length; i++) {
                nums[i] = nums[i] * nums[i];
            }
            for(int i = 0; i < nums.length; i++) {
                for(int j=i+1; j < nums.length; j++) {
                    if(nums[i] > nums[j]) {
                        int tmp = nums[i];
                        nums[i] = nums[j];
                        nums[j] = tmp;
                    }
                }
            }
            return nums;
    }
}

上面冒泡排序让算法的时间复杂度变成了O(n+n^2),可以换成快速排序。如果您还不知道什么是快速排序，可以参考博客:快速排序

class Solution {
    public int[] sortedSquares(int[] nums) {
            for(int i = 0; i < nums.length; i++) {
                nums[i] = nums[i] * nums[i];
            }
            quickSort(nums, 0, nums.length-1);
            return nums;
    }

    public void quickSort(int[] nums,int left, int right) {
        if(left > right) {
            return;
        }
        int i = left, j = right, base = nums[i];
        while(i != j) {
            while(i<j && nums[j] >= base ) {
                j--;
            }
            while(i<j && nums[i] <= base) {
                 i++;
            } 
            int tmp = nums[i];
            nums[i] = nums[j];
            nums[j] = tmp;
        }
        nums[left] = nums[i];
        nums[i] = base;
        quickSort(nums, left, i -1);
        quickSort(nums, i + 1, right);
    }
}

上面的时间复杂度是O(n + n*logn).

解法2：双指针法
注意到数组本来是有序的，平方和后，大的数在两边，小的数在中间，可以采用两个指针在两边遍历，把大的数移到另一个新的数组。

class Solution {
    public int[] sortedSquares(int[] nums) {
            for(int i = 0; i < nums.length; i++) {
                nums[i] = nums[i] * nums[i];
            }

            int i = 0;
            int j = nums.length - 1;
            int[] result = new int[nums.length];
            int index = nums.length - 1;
            while(i <= j) {
                if(nums[i] >= nums[j]) {
                    result[index--] = nums[i];
                    i++;
                } else {
                    result[index--] = nums[j];
                    j--;
                }
            }
            return result;
    }   
}

此时的时间复杂度为O(2*n),空间复杂度为O(n),注意到数据的平方操作和排序可以用一次遍历解决，优化如下。

class Solution {
    public int[] sortedSquares(int[] nums) {
            int i = 0;
            int j = nums.length - 1;
            int[] result = new int[nums.length];
            int index = nums.length - 1;
            while(i <= j) {
                if(nums[i] * nums[i] >= nums[j] * nums[j]) {
                    result[index--] = nums[i] * nums[i];
                    i++;
                } else {
                    result[index--] = nums[j] * nums[j];
                    j--;
                }
            }
            return result;
    }
    
}

总结下：

1.数组的最优解法需要观察数据的特点，比如这道题目的数组元素有两边大，中间小的特点
2.双指针法灵活、高效、好用

leetcode-T209 长度最小的子数组

法1：暴力解决法
从第一个元素开始遍历数组元素累加，当累加值到达target记录为最小长度。再从第二个元素，第三个元素开始做同样操作，并且不断对比最小长度是否需要进行更新。其时间复杂度为O(n^2),空间复杂度为O(1)

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int minLen = Integer.MAX_VALUE;
        for (int i = 0; i < nums.length; i++) { 
            int sum = 0;
            int l = 0;
             for( int j = i;j < nums.length;j++) {
                 sum += nums[j];   
                 l++;
                 if(sum >= target) {
                 // minLen = l < minLen ? l : minLen;
                     if(l < minLen) {
                        minLen = l;
                     }
                     break;
                 }
             }
            
        }
        // return minLen == Integer.MAX_VALUE ? 0 : minLen;
        if(minLen == Integer.MAX_VALUE) {
            minLen = 0;
        }
        return minLen;
       
    }
}

法2：滑动窗口法
所谓滑动窗口，就是不断的调整子序列的起始位置和终止位置，从而得出我们想要的结果。其实，滑动窗口法还是一种双指针法。

💐使用滑动窗口法需要确定几点
1.窗口(两个指针)内是什么
2.窗口起始位置(起始指针)怎么移动
3.窗口结束位置(结束指针)怎么移动

我们来回答下。

1.窗口内容就是满足其和>=target的最小树组
2.如果当前窗口满足条件，起始位置就需要向前移动(缩小窗口)
3.窗口的结束指针就是数组的遍历索引。

可以看出，解题的关键就在于窗口的起始位置如何移动？

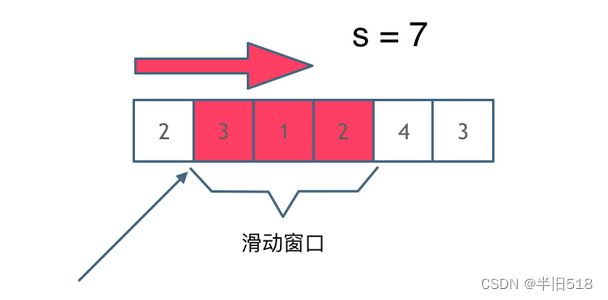
其核心逻辑如下。

 while(sum >= target) {
      subLen = j -i + 1;
      minLen = minLen < subLen ? minLen : subLen;
      sum -= nums[i++];
}

来看完整代码。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int minLen = Integer.MAX_VALUE;
        int sum = 0;
        int i = 0;
        int subLen = 0;
        for (int j = 0; j < nums.length; j++) { 
            sum += nums[j];
            while(sum >= target) {
                subLen = j -i + 1;
                minLen = minLen < subLen ? minLen : subLen;
                sum -= nums[i++];
            }
            
        }

       return minLen == Integer.MAX_VALUE ? 0 : minLen;
       
    }
}

它的时间复杂度是多少呢？虽然这个方法同样有一个for，一个while，但是每个数组元素只被操作了两次，也就是滑动窗口进来操作了一次，滑动窗口除去操作了一次，时间复杂度是O(n)，妙阿。

Leetcode-T59 螺旋矩阵II

这道题目其实不涉及太多算法，却能很好的考察思维能力和编程能力。题目中做的事情无非就是对数组进行上、下、左、右四个方向的遍历，遍历要想不重复、不遗漏一定需要有合理的规则。

我们先以三阶矩阵为例子来画下四条边，采取的规则是：左闭右开。

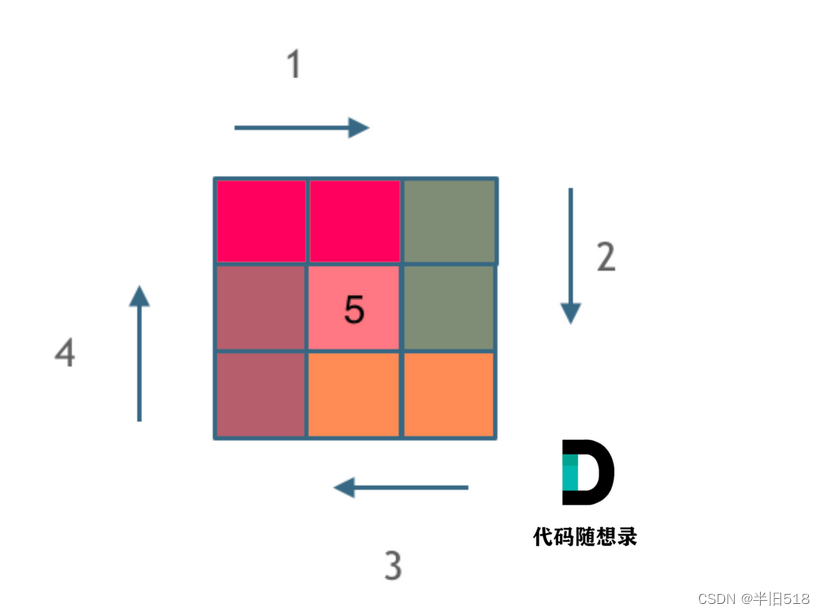
发现没有，定了规则以后就不乱了，三阶矩阵画边就是每个边界走两步。

边画好了，中间填下最后一个数就好了。

这个时候思维再进一步，四阶矩阵要怎么画？

第一步，四阶矩阵先画边。

第二步，剩下的就是一个三阶矩阵。

class Solution {
    public int[][] generateMatrix(int n) {
       int [][] matrix = new int[n][n]; // 定义存储的二维数组
       int start = 0; // 定义起始位置
       int round = 0; // 控制循环次数
       int i,j; // 指针
       int count = 1; // 定义填充数字
       while(round++ < n/2) { 
           // 右
          for(j = start;j < n - round; j++) {
              matrix[start][j] = count++;
          }
           // 下
          for(i = start; i < n - round; i++) {
              matrix[i][j] = count++;
          }
       
           // 左
            for(; j >= round; j--) {
                matrix[i][j] = count++;
            }

            // 上
            for(; i >= round; i--) {
                matrix[i][j] = count++;
            }
            // 更新起始位置
            start++;
       }
    
       // n为奇数时，要单独填充最后一个元素
       if(n % 2 == 1) {
         matrix[start][start] = count;
       }
        return matrix;
    }
}