-
【论文笔记】An Image Patch is a Wave: Phase-Aware Vision MLP
声明
不定期更新自己精度论文,通俗易懂,初级小白也可以理解
涉及范围:深度学习方向,包括 CV、NLP、Data Fusion、Digital Twin
 论文标题:An Image Patch is a Wave: Phase-Aware Vision MLP
论文标题:An Image Patch is a Wave: Phase-Aware Vision MLP论文链接:https://arxiv.org/abs/2111.12294
论文代码:http://The shttps: //github.com/huawei-noah/CV-Backbones/ tree/master/wavemlp_pytorch
发表时间: 2022年4月
创新点
1、将 patch 以一种动态形式 (wave) 输入,以此实现不同的 patch 之间的非线性联系
Abstract
在计算机视觉领域,最近的工作表明,主要由全连接层堆叠的纯 MLP 架构可以实现与 CNN 和 Transformer 竞争的性能。视觉 MLP 的输入图像通常被拆分为多个令牌(补丁),而现有的 MLP 模型直接将它们以固定的权重聚合,忽略了来自不同图像的令牌的不同语义信息。为了动态聚合令牌,我们建议将每个令牌表示为具有振幅和相位两部分的波函数。幅度是原始特征,相位项是根据输入图像的语义内容而变化的复数值。引入相位项可以动态调节 MLP 中令牌和固定权重之间的关系。基于类波令牌表示,我们为视觉任务建立了一种新颖的 WaveMLP 架构。大量实验表明,在图像分类、对象检测和语义分割等各种视觉任务上,所提出的 Wave-MLP 优于最先进的 MLP 架构。
Method
通俗上讲,CV 领域的发展历程是从卷积到 Transformer 的。而 Transformer 的核心原理是把图片分解成每一个 patch,然后计算所有的 patch 之间的相似度,相近的则权重变大,而 MLP 也是在做同样一件事,不过 MLP 模型聚合了具有固定权重的不同 patch(或token),导致会忽略他们之间的差异特征,作者基于此,将 patch 以波的形式输入,初相可以理解成原始特征,振幅,表示非线性的差异特征,解决上述问题。
作为为什么会有这个思想呢?作者受到量子力学的启发,这个地方就不在这里细说了,感兴趣的可以查看原文,参看参考文献。
相位和振幅的概念,属于数学中,复数或三角函数的理解。(属于个人理解)
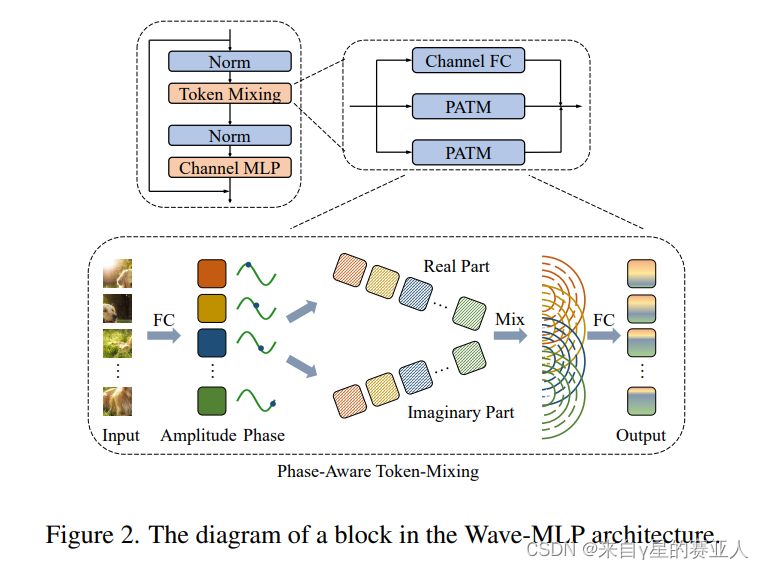
PATM 的构造分为 Real Part(实部),Imaginary Part(虚部),上图结构图很简单,这里属于一种数学运算,
我个人理解:Real Part 可以理解成 MLP 聚合的权重信息,而 Imaginary Part 可以理解成为他们之间的差异关系。
附,计算公式,如下图
感兴趣的同学们,可以自行看一下原文,我没看太仔细看

zj:表示输入的向量
Wc:表示一个可以学习的权重,意义为 MLP 进行权重学习
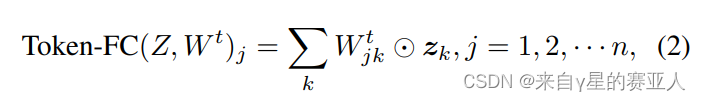
Wt:表示第 j 个的 patch 的混合权重(可以理解为虚部的权重特征)
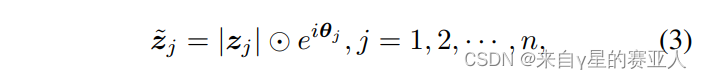 zj:上文提过,是真实的特征向量
zj:上文提过,是真实的特征向量ei:是一个周期函数,这里逐元素相乘,我理解是给每一特征加上波的概念,增加虚部(差异特征)

一系列的数学运算,数学好的,可以在评论区,写上自己的理解
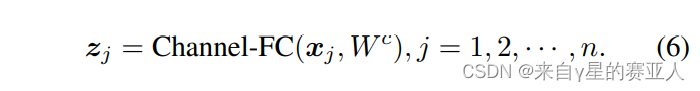
xj:是作为 patch 的输入,上文的 zj 是作为每个函数的自变量的意思

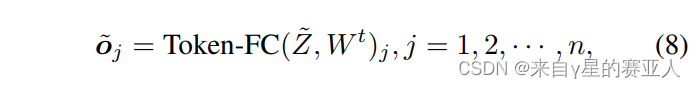
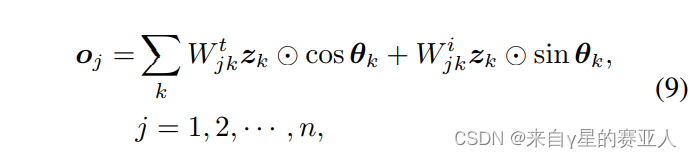
Experiments
实验目标:将提出的 Wave-MLP 架构与 ImageNet 上现有的视觉 MLP 模型进行比较
实验结果:有明显优势
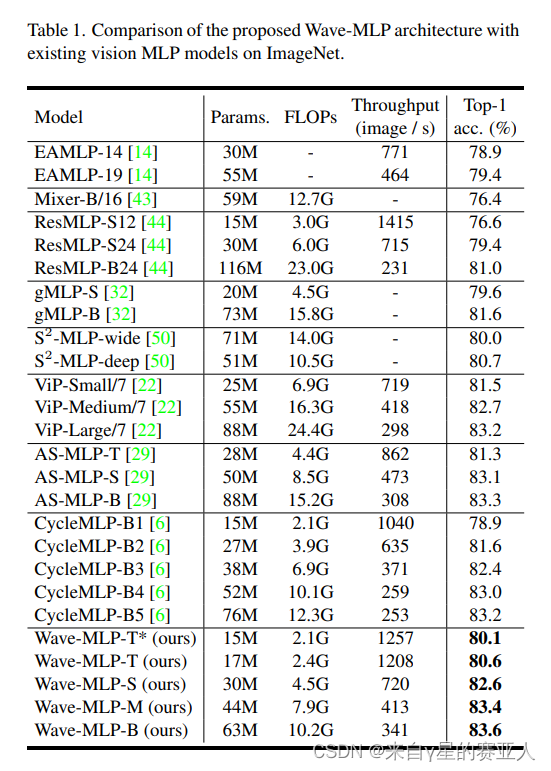
实验目标:表 2. 提出的 Wave-MLP 架构与 ImageNet 上的 SOTA 模型的比较
实验结果:结果与最先进的 transformer 模型,有略微优势
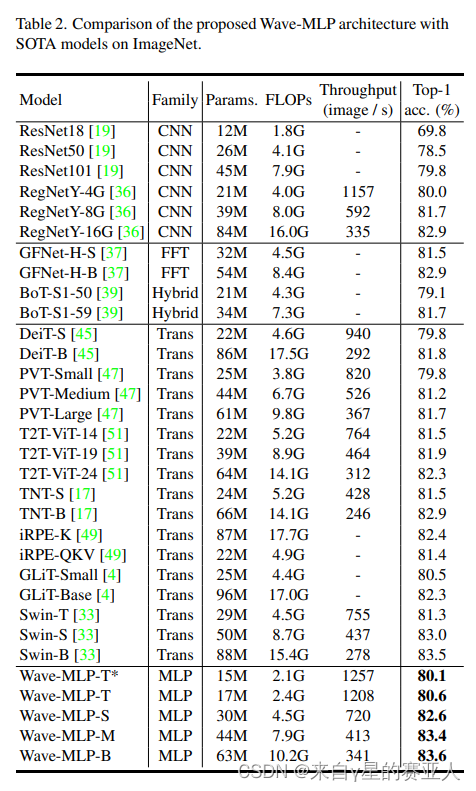
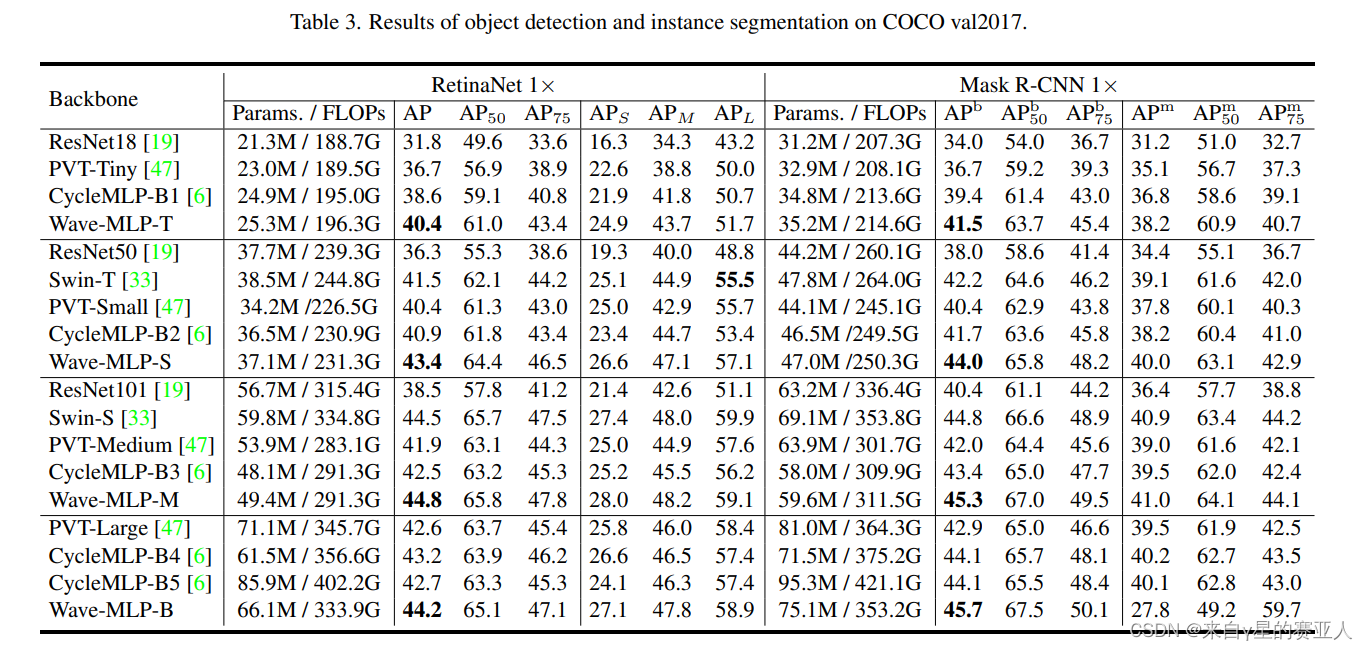
实验目标:COCO val 2017 上的对象检测和实例分割结果
实验结果:效果最好
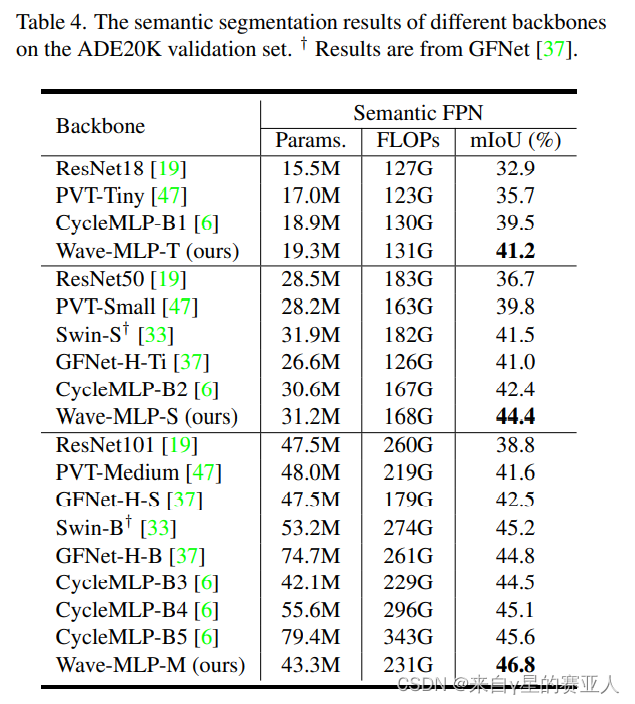
实验目标:ADE20K 验证集上不同主干的语义分割结果
实验结果:效果最好
写在最后
Wave-MLP 可以理解成,一种新的 MLP 结构,可以直接应用在我们的神经网络之中,北大和华为方舟,真是大牛云集呀!!!
-
相关阅读:
逻辑漏洞----任意账号注册
git基本命令
Mybatis执行器
C++入门知识
[SystemC]SystemC中的模块和程序
VS Code里使用Debugger for Unity插件进行调试(2023最新版)
【经典面试题-LeetCode134:加油站问题(Java实现)】
篇12:samba服务器的搭建与配置
MySQL学习系列(4)-每天学习10个知识
Catch That Row(广度优先搜索)
- 原文地址:https://blog.csdn.net/m0_58678659/article/details/127030677