数据结构与算法9-排序算法：选择排序、冒泡排序、快速排序

目录

选择排序

冒泡排序

快速排序

---

ok，最近几天有点事情，今天继续整理一部分排序算法

上次分享了插入、希尔、归并排序

数据结构与算法8-排序算法：插入排序、希尔排序、归并排序_是菜菜的小严惜哎的博客-CSDN博客排序算法：插入排序、希尔排序、归并排序https://blog.csdn.net/weixin_46097842/article/details/126834186

今天分享选择、冒泡、快排

选择排序

选择排序和插入排序的思路是比较相似的，也分为已经排序的部分和没有排序的部分，每次选择排序会从未排序的部分找到最小的元素，将其放到已经排序的末尾，但是它不像选择排序那样移动数据，它会交换位置

比如 1 3 4 5 0，执行的时候就是就是 0 3 4 5 1

我们写一段代码实现一下

/**
 * @author create by YanXi on 2022/9/19 16:44
 * @email best.you@icloud.com
 * @Description: 选择排序
 */
public class SelectSort {
 
    public static void main(String[] args) {
        int a[] = {11, 4, 12, 6, 0, 23, 1, 6, 8, 23, 1, 6};
        int n = a.length;
        for (int i = 0; i < n; i++) {
            int minIndex = i;
            for (int j = i + 1; j < n; j++) {
                if (a[minIndex] > a[j]) {
                    minIndex = j;
                }
            }
            swapProperties(a, i, minIndex);
        }
        for (int i = 0; i < n; i++) {
            System.out.print(a[i] + ",");
        }
    }
 
    public static void swapProperties(int a[], int index1, int index2) {
        int tmp = a[index1];
        a[index1] = a[index2];
        a[index2] = tmp;
    }
 
}

这就是实现出来的样子

代码就是我们上面说的顺序，每次都找到没排序的最小的那部分，然后交换位置

写完之后，我们可以发现，时间复杂度是O(n^2)，两层循环，都得走

而空间复杂度就是O(n)，交换次数是n次

在稳定性上，选择排序也是不稳定的，因为存在交换位置，所以很可能前面的就会被换到后面，而后面的会被换到前面

冒泡排序

现在我们来进行冒泡排序的总结查看

冒泡排序，和冒泡两个字很像，一级一级往外蹦跶

冒泡排序的思路就是，每次冒泡操作都对比相邻的两个元素，判断是否需要交换位置，这样重复n次，就完成了排序工作

举个例子

1  5  2  0  9

首先是1和5比较，不用交换，接着5和2比较，交换位置

1  2  5  0  9

然后，因为5和2交换了位置，继续比较，5和0比较，交换位置

这样，以此类推，直到这次到数据结束，第一次冒泡结束，紧接着开始第二次

注意，不要乱，这个比较交换的可以理解为索引位，挨个索引位比较，千万不要第一个和第二个比较了，第三个和第四个比较，第一个和第二个比较完了，接下来是第二个和第三个比较

搞个代码实现一下子

/**
 * @author create by YanXi on 2022/9/19 20:56
 * @email best.you@icloud.com
 * @Description: 冒泡排序
 */
public class BubbleSort {
 
    public static void main(String[] args) {
        int a[] = {11, 4, 12, 6, 0, 23, 1, 6, 8, 23, 1, 6};
        int n = a.length;
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n - 1 - i; j++) {
                if (a[j] > a[j + 1]) {
                    int tmp = a[j];
                    a[j] = a[j + 1];
                    a[j + 1] = tmp;
                }
            }
        }
        for (int i = 0; i < n; i++) {
            System.out.print(a[i] + ",");
        }
    }
 
}

这儿第二个循环可能有的朋友们会懵一下，为什么 j < n - 1 - i，这个也好理解，j < n -1 明白吧，是为了防止索引越界的，而为什么要减去 i，可能这儿会有点乱，减去 i，是因为没必要，经过前面的循环，i前面已经排序过了，全都冒泡了一遍了，还从头来干啥

第一层循环控制从哪儿开始冒泡，第二层循环开始挨个往后进行冒泡的过程

很显然，冒泡的时间复杂度也是O(N^2)，而空间复杂度也就是O(n)

交换的次数，这就比较多了，最坏的情况就是每个都得换

当然，也可以看到这是个稳定的排序算法，不过也不是一定的，我们写的代码是大于的时候交换，如果换成大于等于交换，那这个就就不稳定了

我们可以做一个优化，当没有交换的时候，我们直接退出

想一想为什么要这么加

既然没有发生交换，是不是意味着，后面都是有序的，后面既然都是有序的了，那还冒泡个啥

快速排序

快排，是一个在实际面试中搞得比较多的，也不是冒泡和选择那么简单的

首先，快排称为快排，那它必须得快

快排，首先要有一个基准数，基准数的好坏往往决定了快排效率的高低，如果不知道选哪个，一般选第一个

快排所作的，就是在完成分区后，比基准数大的都在右边，比基准数小的都在左边，然后只要利用递归，两遍的分区各自再进行这样分区排序，到最后，就排序完成了

这样可能有点抽象，我们来举个例子，用实际的例子比较明确一点，这个例子不是快排唯一的实现思路，只不过我觉得是比较清晰明了的，而且搜了一下，好像用这种思路的比较多

首先，有这样一个等待排序的玩意

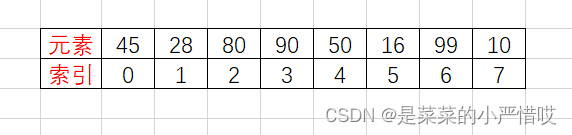
我们开始快排的思路，首先，选一个基准数，不知道选啥，那就第一个，也就是 index0 的45

注意，接下来就是快排的比较方法了！

我们从后往前找，找到比基准数小的，进行位置交换，也就是说，从后往前找，找到比45小的，就进行交换，交换后的结果如下

紧接着，我们再从前往后，找到比基准数大的，进行交换，注意，基准数指的是元素，并非索引位置，也就是说，45从 index0 调到了 index7，基准数也还是 45

然后我们从前往后，28 小于 45，不管，80 大于 45，交换

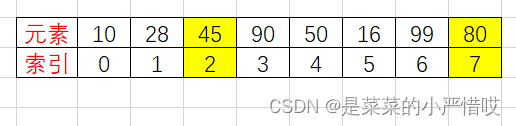
然后再从后往前找比基准数 45 小的，交换，这样前后前后，到最后，我们可以得到这样一个序列

这个时候，45 作为基准数已经调整完了，仔细看，是不是 45 的左边，都比它小，而右边，都比它大

这个时候，如果我们把 45 的左边当做一个序列，右边当做一个序列，采用相同的做法，进行排序呢？到最后，左边有序，右边有序，整体有序，over

这，就是快排的思路和用法

怎么样能想明白不，如果想不明白为什么要一前一后，那就和最后的结果联系起来，小于的都在左边，大于的都在右边

快排和归并排序很像，但是，归并是先分后排后合，而快排，边分边排，分到最后，就有序了

类似于尾递归，每次排的时候，结果都传下去一样

--------

这个地方可能有一个问题，为什么要找一个小的，找一个大的，而不是一次性找完它？

思考这样一个问题，如果快排基准数取的不太好，比如我们上面的例子，取到了 99，然后每次都很不巧，取到了最大的数字，那每次，右边都是一个，左边是剩下的，就是一条链下去的，是个O(n)，而如果取的好，最好的情况，可能是左右一样，是个二分，而二分，就只有O(logn)

so，优化快排的话，其实就是优化基准数

/**
 * @author create by YanXi on 2022/9/25 22:27
 * @email best.you@icloud.com
 * @Description: 快速排序
 */
public class QuiklySort {
 
    public static void main(String[] args) {
        int a[] = {11, 4, 12, 6, 0, 23, 1, 6, 8, 23, 1, 6};
        sort(a, 0, a.length - 1);
        System.out.println(Arrays.toString(a));
    }
 
 
    public static void sort(int data[], int left, int right) {
        // 注意不要用data[0]，因为这是个递归，取0不对
        int base = data[left];
        // 从左边找
        int ll = left;
        // 从右边找
        int rr = right;
        while (ll < rr) {
            // 从后往前找小的数
            while (ll < rr && data[rr] >= base) {
                rr--;
            }
            // 如果上面的循环都走完了，左边还小于右边，说明是while循环后半部分终止，false了，说明找到了比基准数小的，可以交换位置
            if (ll < rr) {
                data[ll] ^= data[rr];
                data[rr] ^= data[ll];
                data[ll] ^= data[rr];
                ll++;
            }
 
            // 从前往后找大的数
            while (ll < rr && data[ll] <= base) {
                ll++;
            }
            // 如果上面的循环都走完了，左边还小于右边，说明是while后半部分终止，也就是说，遇到了大于基准数的，就可以交换位置了
            if (ll < rr) {
                data[ll] ^= data[rr];
                data[rr] ^= data[ll];
                data[ll] ^= data[rr];
                rr--;
            }
        }
        if (left < ll) {
            // 比较左边分区，因为基准数不用动，也不用继续参加左边排序，所以直接减一，去掉它
            sort(data, left, ll - 1);
        }
        if (ll < right) {
            // 比较右边分区,因为基准数不用动，也不用继续参加右边排序，所以直接加一，去掉它
            sort(data, ll + 1, right);
        }
    }
 
 
}

时间复杂度来说，快排的时间复杂度最好是 nlogn，而最坏的情况，就是 n^2

空间复杂度，我们没有开辅助变量，也就是 O(n)

至于稳定性，快排是不稳定的，这个也很明显

以上就是这次的排序算法分享

bye~