广义表的相关概念及其性质

一、广义表的相关概念

1、广义表的定义：广义表(又称列表Lists)是n>=0个元素a0,a1, ... ,an的有限序列，其中每一个ai或者是原子，或者是一个广义表。这种拓宽了的线性表就是广义表。

2、广义表通常记作: LS=(a1, a2,...,an)

其中: LS为表名，n为表的长度， 每一个ai为表的元素。

习惯上,一般用大写字母表示广义表，小写字母表示原子。

3、表头:若LS非空(n≥1 ),则其第一个元素a1就是表头。

记作head(LS) = a1。            注:表头可以是原子，也可以是子表。

4、表尾:除表头之外的其它元素组成的表。

记作tail(LS)= (a2,... ,an)。                       注:表尾不是最后一个元素，而是一个子表。

二、广义表的性质

1、广义表中的数据元素有相对次序：一个直接前驱和一个直接后继

2、广义表的长度定义为最外层所包含元素的个数

如C=(a, (b, c)) 是长度为2的广义表。

3、广义表的深度定义为该广义表展开后所含括号的重数

A=(b, c)的深度为1，B= (A, d)的深度为2，C=(f B, h)的深度为3。

注意: "原子” 的深度为0; "空表” 的深度为1

4、广义表可以为其他广义表共享。如:B=（A)，广义表B就共享表A。在B中不必列出A的值，而是通过名称来引用。

5、广义表可以是一个递归的表。 如: F=(a,F)=(a, (a, (a...)))

注意:递归表的深度是无穷值，长度是有限值。

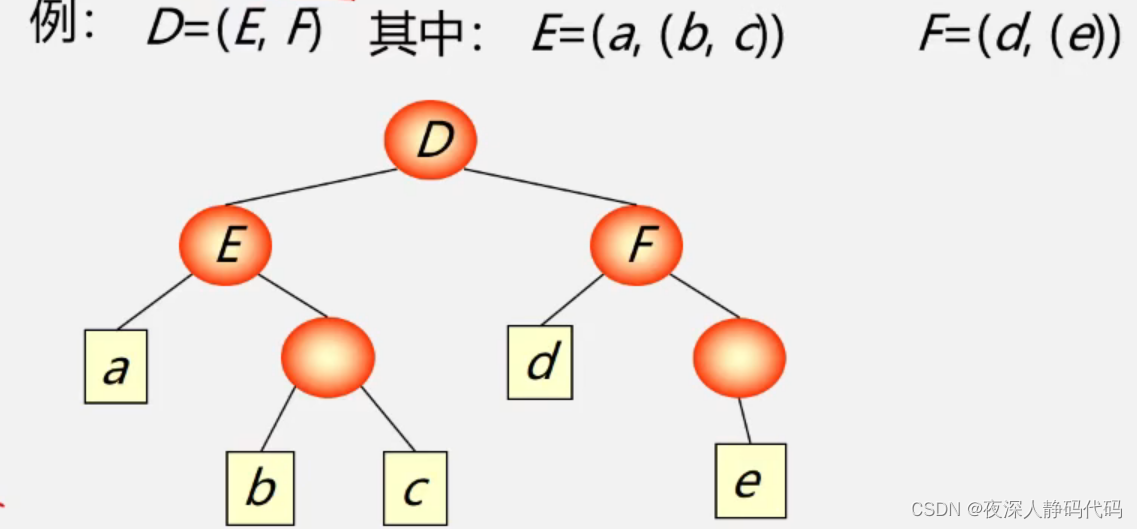
6、广义表是多层次结构，广义表的元素可以是单元素，也可以是子表，而子表的元素还可以是子表，...。可以用图形象地表示。如下图所示：

 三、广义表与线性表的区别

广义表可以看成是线性表的推广，线性表是广义表的特例。

广义表的结构相当灵活， 在某种前提下，它可以兼容线性表、数组、树和有向图等各种常用的数据结构。

当二维数组的每行(或每列)作为子表处理时，二维数组即为一个广义表。

另外，树和有向图也可以用广义表来表示。

由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的特点，而且可有效地利用存储空间，因此在计算机的许多应用领域都有成功使用广义表的实例。