计算空间物体包围球的两种算法实现

1. 概述

在进行二维空间几何运算的之前，往往会用包围盒进行快速碰撞检测，从而筛掉一些无法碰撞到的可能。而在三维中，比较常用的就是包围球了。当然，如何计算包围球是一个问题。

2. 详论

2.1. naive算法

一个最简单的思路就是，计算空间顶点在X、Y、Z方向上的最大值和最小值，那么就可以得到8个顶点组成的包围盒。取包围球中心为包围盒中心点，而包围球半径有的人认为可以取中心点到八个顶点的最大距离——这样其实并不严密。最好还是计算中心点到所有顶点距离的最大值：

void BoundingSphere::GetBoundingSphereNative(const std::vector& pointList)
{
    if (pointList.empty())
    {
        return;
    }

    Vec3d minPoint(DBL_MAX, DBL_MAX, DBL_MAX);
    Vec3d maxPoint(-DBL_MAX, -DBL_MAX, -DBL_MAX);

    size_t vertexCount = pointList.size();
    for (size_t vi = 0; vi < vertexCount; vi++)
    {
        if (minPoint.x() > pointList[vi].x())
        {
            minPoint.x() = pointList[vi].x();
        }

        if (minPoint.y() > pointList[vi].y())
        {
            minPoint.y() = pointList[vi].y();
        }

        if (minPoint.z() > pointList[vi].z())
        {
            minPoint.z() = pointList[vi].z();
        }

        if (maxPoint.x() < pointList[vi].x())
        {
            maxPoint.x() = pointList[vi].x();
        }

        if (maxPoint.y() < pointList[vi].y())
        {
            maxPoint.y() = pointList[vi].y();
        }

        if (maxPoint.z() < pointList[vi].z())
        {
            maxPoint.z() = pointList[vi].z();
        }
    }

    Vec3d naiveCenter = (maxPoint + minPoint) / 2;
    double naiveRadius = 0;
    for (size_t vi = 0; vi < vertexCount; vi++)
    {
        naiveRadius = std::max(naiveRadius, (pointList[vi] - naiveCenter).length());
    }
    data = { naiveCenter.x(), naiveCenter.y(), naiveCenter.z(), naiveRadius };
}

这个算法的思路比较简单，所以称之为naive算法。

2.2. ritter算法

另外一种算法是一个名为ritter提出来的，所以称为ritter算法。

首先计算出X方向上距离最远的两个点，Y方向上距离最远的两个点以及Z方向上距离最远的两个点。以这三个距离最远的范围作为初始直径，这三个距离的中心点作为初始球心。

然后依次遍历所有点，判断点是否在这个包围球内。如果不在，则更新包围球。如下图所示：

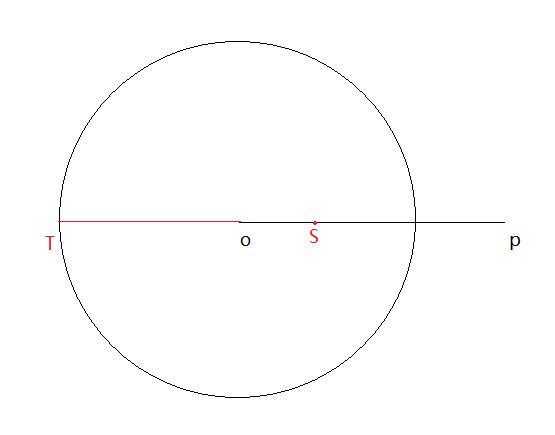
如果点P在我们的之前得到的包围球之外，那么延长点P与球心O的直线与球相较于T点，很显然，新的直径应该是点T与点P的一半：

\[R_{current} = \frac{|\overrightarrow{PT}|}{2} = \frac{|\overrightarrow{OP}| + |\overrightarrow{OT}|}{2} \]

令点T与点P的中心点为S，也就是新的球心位置。关键就是求向量\(\overrightarrow{OS}\)，从而将球心O移动到新的球心S。

显然，向量\(\overrightarrow{OS}\)的距离还是很好求的，只新的包围球半径与之前包围球的半径之差：

\[|\overrightarrow{OS}| = R_{current} - R_{previous} \]

而向量\(\overrightarrow{OP}\)是已知的，根据向量关系，可求得：

\[\overrightarrow{OS} = \frac{|\overrightarrow{OS}|}{|\overrightarrow{OP}|}\overrightarrow{OP} \]

最后将之前的球心O移动向量\(\overrightarrow{OS}\)，就是新的包围球的球心位置了。

具体的算法代码实现：

void BoundingSphere::GetBoundingSphereRitter(const std::vector& pointList)
{
    //
    Vec3d minPoint(DBL_MAX, DBL_MAX, DBL_MAX);
    Vec3d maxPoint(-DBL_MAX, -DBL_MAX, -DBL_MAX);
    size_t minX = 0, minY = 0, minZ = 0;
    size_t maxX = 0, maxY = 0, maxZ = 0;
    size_t vertexCount = pointList.size();

    for (size_t vi = 0; vi < vertexCount; vi++)
    {
        if (minPoint.x() > pointList[vi].x())
        {
            minPoint.x() = pointList[vi].x();
            minX = vi;
        }

        if (minPoint.y() > pointList[vi].y())
        {
            minPoint.y() = pointList[vi].y();
            minY = vi;
        }

        if (minPoint.z() > pointList[vi].z())
        {
            minPoint.z() = pointList[vi].z();
            minZ = vi;
        }

        if (maxPoint.x() < pointList[vi].x())
        {
            maxPoint.x() = pointList[vi].x();
            maxX = vi;
        }

        if (maxPoint.y() < pointList[vi].y())
        {
            maxPoint.y() = pointList[vi].y();
            maxY = vi;
        }

        if (maxPoint.z() < pointList[vi].z())
        {
            maxPoint.z() = pointList[vi].z();
            maxZ = vi;
        }
    }

    //
    double maxLength2 = (pointList[maxX] - pointList[minX]).length2();
    Vec3d min = pointList[minX];
    Vec3d max = pointList[maxX];
    {
        double yMaxLength2 = (pointList[maxY] - pointList[minY]).length2();
        if (maxLength2 < yMaxLength2)
        {
            maxLength2 = yMaxLength2;
            min = pointList[minY];
            max = pointList[maxY];
        }

        double zMaxLength2 = (pointList[maxZ] - pointList[minZ]).length2();
        if (maxLength2 < zMaxLength2)
        {
            maxLength2 = zMaxLength2;
            min = pointList[minZ];
            max = pointList[maxZ];
        }
    }

    //
    Vec3d ritterCenter = (min + max) / 2;
    double ritterRadius = sqrt(maxLength2) / 2;
    for (size_t i = 0; i < vertexCount; i++)
    {
        Vec3d d = pointList[i] - ritterCenter;
        double dist2 = d.length2();

        if (dist2 > ritterRadius * ritterRadius)
        {
            double dist = sqrt(dist2);
            double newRadious = (dist + ritterRadius) * 0.5;
            double k = (newRadious - ritterRadius) / dist;
            ritterRadius = newRadious;

            Vec3d temp = d * k;
            ritterCenter = ritterCenter + temp;
        }
    }

    data = { ritterCenter.x(), ritterCenter.y(), ritterCenter.z(), ritterRadius };
}

2.3. 其他

理论上来说，ritter算法的实现要优于naive算法，能够得到更加贴合的包围球。当然理论只是理论，具体的实现还要看最终的效果。根据文献2中所说，经过Cesium的比对测试，19%的情况下，ritter算法的效果比naive算法差；11%的情况下，ritter算法的效果会比naive算法好。所以在Cesium中，包围球的实现是把两者都实现了一遍，然后取半径较小的结果。

3. 参考

1. 3D空间包围球(Bounding Sphere)的求法
2. Cesium原理篇：3最长的一帧之地形(2：高度图)