推荐算法：HNSW算法简介

• 推荐算法：HNSW算法简介
  • 1. HNSW算法概述
  • 2. HNSW算法原理
    • 1. Delaunay图
    • 2. NSW算法
    • 3. HNSW算法
  • 3. HNSW算法实现
    • 1. hnswlib
    • 2. nmslib
    • 3. faiss
  • 4. 参考链接

• 文献链接：Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs

1. HNSW算法概述

HNSW（Hierarchical Navigable Small Word）算法算是目前推荐领域里面常用的ANN（Approximate Nearest Neighbor）算法了。

其目的就是在极大量的候选集当中如何快速地找到一个query最近邻的$k$个元素。

要找到一个query的k个最近邻元素，一个朴素的思想就是我去计算这个query和所有的总量$N$个候选元素的距离，然后选择其中的前$k$个最小元素，这个经典算法的算法复杂度是$O(Nlog(k))$，显然这个算法复杂度实在是太高了，无法适用于实际的使用场景。

而要解决这个问题，可以有多种实现方法，这里所要说的HNSW算法就是目前比较常用的一种搜索算法，它算是其前作NSW算法的一个升级版本，但是两者的本质都是基于一个朴素的思路，就是通过图连接的方式给所有的$N$个候选元素事先地定义好一个图连接关系，从而可以将前述的算法复杂度当中的$N$的部分给减小掉，从而优化整体的检索效率。

其整体的一个图结果可以用下图进行表达：

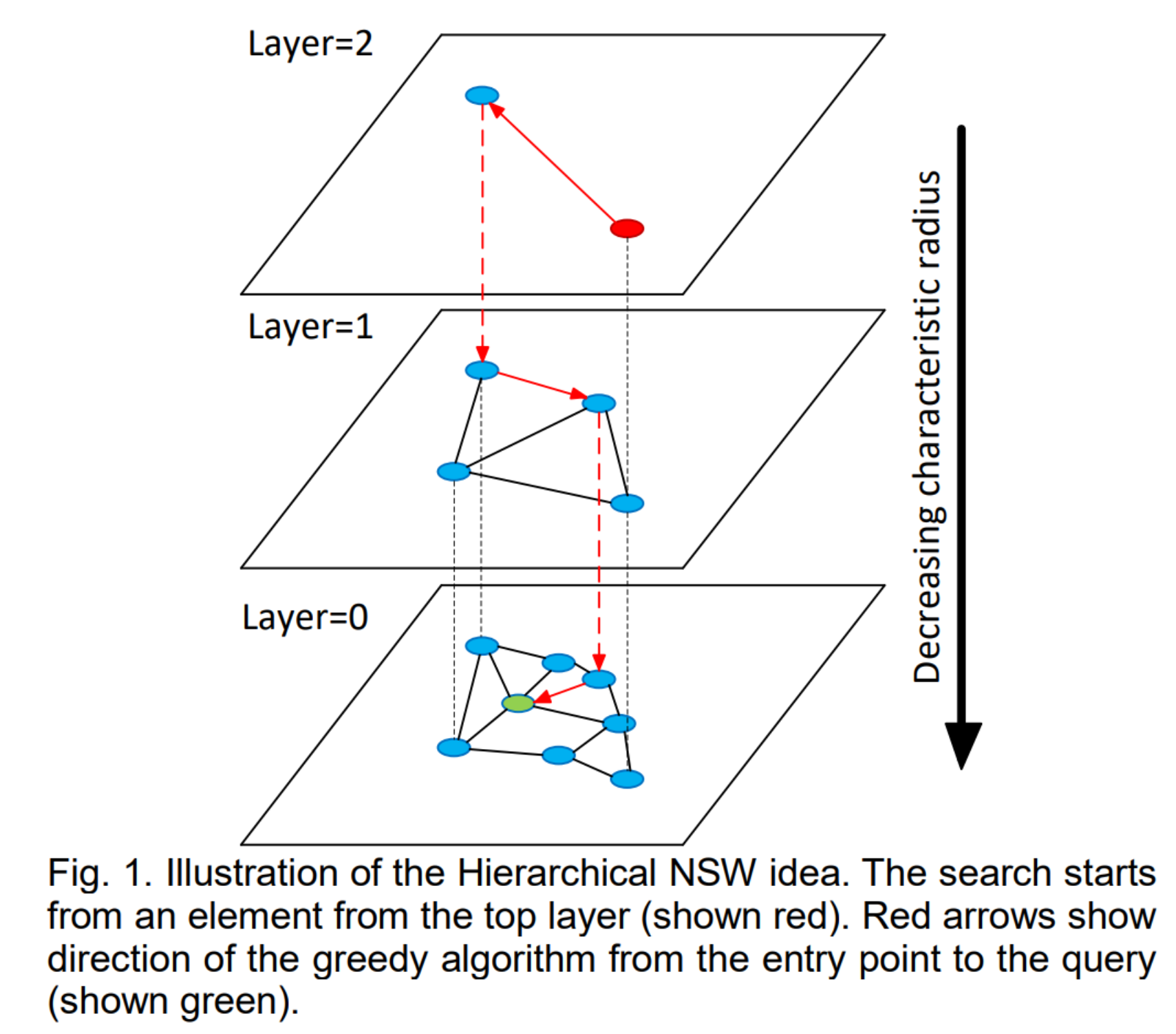
我们在下面的第二小节当中会对这个算法进行具体的展开描述，而在第三小节当中我们会基于当前几个常见的开源库来对hnsw算法进行简单的实现。

2. HNSW算法原理

现在，我们来看一下HNSW算法的具体原理。

如前所述，HNSW算法是其前作NSW算法的优化算法，因此，在介绍HNSW算法的细节之前，我们需要首先来介绍一下NSW算法。

而要说明NSW算法，我们又必须要先引入Delaunay图，因为NSW算法本质上是对Delaunay图检索的有一个优化。

因此，下面，我们就分别来依序介绍一下这三部分的内容。

1. Delaunay图

首先，我们来介绍一下Delaunay图。

Delaunay图，或者说Delaunay三角剖分本质上就是将图上的一系列散点组成不相交的三角形，然后使得所有这些三角形中最小角度的最大化。

对于点集$P$的Delaunay三角剖分$DT(P)$具有如下性质：

• 点集$P$当中的任意点均不在Delaunay三角剖分中的任意一个三角形的外接圆当中。

关于Delaunay三角剖分的具体数学描述这里就不多做展开了，有兴趣的读者可以自行查阅相关书籍或者参考链接7, 8。

这里仅仅说明：

• 对于一般的点集$P$，除所有点共线等极少数情况之外，Delaunay三角剖分一般都是存在的。

而对于存在Delaunay三角剖分的点集$P$，我们总可以通过下述构造方法构造Delaunay三角剖分：

1. 取一个外接四边形，使得所有的点均位于这个四边形内部，然后对其构造一个初始的三角剖分$T_0$，它总是存在的；
2. 将点集$P$中的点逐一加入到三角剖分当中，并进行如下调整：
   1. 找出当前三角剖分当中的所有外接圆中包含新插入点$v$的全部三角形；
   2. 将这些三角形的内部边全部删除，然后将边界上的所有顶点均与新的插入点$v$相连接，构成新的三角形，此时构造得到的新的三角剖分即为包含点$v$的Delaunay三角剖分；
3. 删除步骤1中额外加入的4个外接点，并同步移除与之相连的所有边，剩下的图形即为目标点集$P$的一个Delaunay三角剖分。

上述实现方法称之为Bowyer-Watson算法。

综上，我们就给出了一般点集的Delaunay图的构造方法。由此，对于任意点集，我们总能够对其进行三角剖分，构建Delaunay图。特别的，我们可以仿照上述的方法将其扩展至n维向量，因此，对于任意的向量集合，我们都可以对其构造一个Delaunay三角剖分，使得两两向量之间均存在一条通路，即我们对于任意一个目标向量，我们从任意起点出发，一定能够找到和目标向量最相似的这个向量。

但是，Delaunay三角剖分虽然保证了连通性，但是检索效率并不总能够得到保证，且完整构造Delaunay三角剖分图的算法复杂度太高，所以在实际应用当中事实上并无法使用。

2. NSW算法

NSW算法是基于Delaunay三角剖分的一个近似优化，他借鉴了三角剖分的形式，但是并不像三角剖分那么复杂，借用参考链接中各类博客中的说法，他在三角剖分当中增设了高速公路，而不是严格按照Delaunay三角剖分的连接关系进行检索，从而使得可以更加快速地到达目标向量附近，从而获得所求的最相似的k个向量。

不过，NSW算法返回的k个搜索结果事实上只是一个近似的结果，并无法保证就是groudtruth，不过整体上NSW还是可用的。

下面，我们就来简单看一下NSW算法具体是怎么做的。

我们摘录下述参考链接5中的介绍如下：

1. 在候选节点$V$里面随机挑选一个节点$v_i$
2. 将节点$v_i$插入到已经构建好的图中，并构建边。
3. 边构建的规则：找到节点$v_i$最近邻的$f$个邻居，建立$v_i$和这些邻居的边连接。

3. HNSW算法

HNSW算法是在NSW算法之上的更进一步的优化版本。

其核心思路就是在NSW算法的基础上引入跳表来实现分层的思路，从而进一步优化到目标向量的检索速度。

具体而言，就是首先使用全部的向量构造一个nsw图，然后找出其中比较具有代表性的点构成一个上层子图，其节点数目满足指数衰减。

重复上述操作直至只剩下一个输入查询节点。

但是其具体实现上事实上是反过来的，具体来说，就是认为越早输入的点和之前已经输入的点的关联关系越弱。因此，在具体构造方法来说，就是我们不断地对当前层增加新的节点，如果某一层的节点数超过了某一个上限值，就对当前节点往下分出一个新的层，然后对这个层继续进行操作。

我们给出原文献中hnsw构造算法伪代码和检索算法伪代码如下：

1. hnsw构造

   

2. 检索算法

   

3. HNSW算法实现

现在，我们来看一下hnsw算法的具体实现，我们以网上常用的几个开源库为例进行说明。

数据方面，我们使用10000个128维的embedding作为候选集，然后用100个query进行调用考察，具体样例如下：

import numpy as np

dim = 128
num_elements = 10000
num_queries = 100

data = np.float32(np.random.random((num_elements, dim)))
ids = np.arange(num_elements)

queries = np.float32(np.random.random((num_queries,dim)))

另外，我们统一设置hnsw的表格超参如下：

M = 32 
efSearch = 100  # number of entry points (neighbors) we use on each layer
efConstruction = 100 # number of entry points used on each layer during construction

整体上来说，要想要获得更快的构建和检索的速度，那么就需要把这三个超参相对地缩小，反之，要获得更好的召回精度，则需要将这三个超参增大。

1. hnswlib

hnswlib库的链接如下：

• https://github.com/nmslib/hnswlib

使用方面使用pip安装即可，我们给出基于hnswlib的hnsw的实现方法如下：

import hnswlib

# build hnsw
index = hnswlib.Index(space = 'l2', dim = dim)
index.init_index(max_elements = num_elements, ef_construction = efConstruction, M = M)
index.add_items(data, ids)
index.set_ef(efSearch) 

# Query
top_k = 10
preds, distances = index.knn_query(queries, k = top_k)

2. nmslib

同样的，我们给出nmslib的github仓库链接如下：

• https://github.com/nmslib/nmslib

而其具体的python demo实现如下：

import nmslib

# build hnsw
index_time_params = {
    'M': M, 
    'efConstruction': efConstruction
}
index = nmslib.init(method='hnsw', space="l2", data_type=nmslib.DataType.DENSE_VECTOR)
index.addDataPointBatch(data)
index.createIndex(index_time_params, print_progress=True)
query_time_params = {'efSearch': efSearch}
index.setQueryTimeParams(query_time_params)

# query hnsw
top_k = 10
res = index.knnQueryBatch(queries, k = top_k, num_threads = 1)

3. faiss

最后，我们来看一下基于faiss的hnsw的实现，其对应的github仓库链接如下：

• https://github.com/facebookresearch/faiss

不过需要注意的是，faiss库的安装多少有点特殊，需要使用如下命令进行安装：

• cpu版本：pip install faiss-cpu
• gpu版本：pip install faiss-gpu

而其关于hnsw的实现方法上面倒是和上述两个库基本保持一致：

import faiss

# build hnsw
index = faiss.IndexHNSWFlat(dim, M)
index.hnsw.efConstruction = efConstruction
index.hnsw.efSearch = efSearch
index.add(data)

# query hnsw
top_k = 10
distance, preds = index.search(queries, k=top_k)

4. 参考链接

1. Hierarchical Navigable Small Worlds (HNSW)
2. HNSW学习笔记
3. 一文看懂HNSW算法理论的来龙去脉
4. HNSW算法详解
5. HNSW的基本原理及使用
6. ANN召回算法之HNSW
7. HNSW
8. 【计算几何】Delaunay 三角化原理与实现
9. 技术分享：Delaunay三角剖分算法介绍