-
【数据库原理及应用】——关系操作、关系完整性、关系代数(万字大总结)
📖 前言:随着时间的变化,现实世界也在不停地发生变化,因此,各种操作也在不停的更新数据库中的数据,但是这种更新要受到现实世界中许多已有事实的限定和制约,例如,学生选修的课程开设了才能选修,即选课关系中课程号来自于课程关系。这些约束为现实世界的真实需要,任何关系在任何时刻都必须满足这些语义约束。为了方便用户,关系模型为这些限定和制约提供了丰富有效的完整性约束机制。
关系操作是关系数据模型的第二个重要的要素,但关系模型并未在关系数据库管理系统语言中给出具体的语法要求,即不同的关系数据库管理系统可以定义和开发不同的语言来实现这些操作。
关系代数是一种抽象的查询语言,是关系数据库操纵语言的一种传统表达方式,它是由关系的运算来表达查询的。它是处理关系数据库的重要数学基础之一,许多著名的关系数据库语言(如 SQL 等)都是基于关系代数开发的。
🕒 0. 思维导图

🕒 1. 关系的完整性
假设有学生选课数据库:
学生(学号,姓名,性别,专业号,年龄,班长)
课程(课程号,课程名,学分)
选修(学号,课程号,成绩)
专业(专业号,专业名,申办时间)🕘 1.1 关系的三类完整性约束
- 如何保证一个数据(实体)是可识别的?
实体完整性 - 如何由一个数据找到另一个数据?
参照完整性 - 如何保证一个数据的取值合理?
用户定义的完整性
含义:
- 实体完整性和参照完整性:
关系模型必须满足的完整性约束条件;
称为关系的两个不变性,应该由关系系统自动支持; - 用户定义的完整性:
应用领域需要遵循的约束条件,体现了具体领域中的语义约束 ;
🕘 1.2 实体完整性(Entity Integrity)
- 若属性A是基本关系R的主属性,则属性A具有唯一性且不能取空值
- 例:学生(学号,姓名,性别,专业号,年龄,班长), 其中:
学号:唯一;不能取空值
🕤 1.2.1 实体完整性规则的说明
- 实体完整性规则是针对基本关系而言的。一个基本表通常对应现实世界的一个实体集。
- 现实世界中的实体是可区分的,即它们具有某种唯一性标识。
- 关系模型中以主码作为唯一性标识。
- 主码中的属性即主属性不能取空值。主属性取空值,就说明存在某个不可标识的实体,即存在不可区分的实体,这与第(2)点相矛盾,因此这个规则称为实体完整性
🕘 1.3 参照完整性
🕤 1.3.1 关系间的引用
- 在关系模型中实体及实体间的联系都是用关系来描述的,因此可能存在着关系与关系间的引用。

- 学生关系引用了专业关系的主码“专业号”
- 学生关系中的“专业号”值必须是确实存在的专业的专业号,即专业
- 关系中有该专业的记录、
🕤 1.3.2 参照完整性规则的说明
若属性(或属性组) F F F是基本关系R的外码它与基本关系 S S S的主码 K s K_s Ks相对应(基本关系 R R R和 S S S不一定是不同的关系),则对于 R R R中每个元组在 F F F上的值必须为:
- 或者取空值(F的每个属性值均为空值)
- 或者等于S中某个元组的主码值

例3:课程COURSE(课程号,课程名,先行课,学分)
“先行课”属性值可以取两类值:
(1)空值,表示该课程没有先行课
(2)非空值,该值必须是本关系表中确实存在的课程号- 外码不一定要与相应的主码同名
🕘 1.4 用户定义的完整性
- 针对某一具体关系数据库的约束条件,反映某一具体应用所涉及的数据必须满足的语义要求
- 关系模型应提供定义和检验这类完整性的机制,以便用统一的系统的方法处理它们,而不要由应用程序承担这一功能
例:
- 学生成绩需取值[0,100]或[0,150]
- 姓名不能取空值
- 未成年人的定义为不超过18岁
- 人的身高不能超过3米
🕒 2. 关系操作
🕘 2.1 基本关系操作
- 常用的关系操作
- 查询:选择(select)、投影(project)、连接(join)、除(divide)、并(union)、交(intersection)、差(except)
- 数据更新:插入、删除、修改
- 查询是关系操作中最主要的部分
- 选择、投影、并、差、笛卡尔基是5种基本操作
- 关系操作的特点
- 集合操作方式:操作的对象和结果都是集合,一次一集合的方式
🕘 2.2 数据操纵功能
🕤 2.2.1 数据查询(可分解为三种基本操作)
- 一个关系内属性的指定(列的选择);
- 一个关系内元组的指定(行的选择);
- 两个或多个关系的合并
数据执行的算法如下:
①. 如果查询来自一个关系R,则直接执行②;如果查询来自两个或者多个关系,则首先执行 3.(如果是多于两个的关系,可能要多次执行 3.),直至将两个或多个关系合并成一个关系R;
②. 从关系R中检索出满足条件 1. 2. 的数据。❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页🕤 2.2.2 数据插入
插入操作
🕤 2.2.3 数据删除
先选择后删除
🕤 2.2.4 数据修改
先删除后插入
🕘 2.3 关系数据库语言的分类
- 关系代数语言
用对关系的运算来表达查询要求;
代表:ISBL; - 关系演算语言:用谓词来表达查询要求;
- 元组关系演算语言
谓词变元的基本对象是元组变量;
代表:APLHA, QUEL; - 域关系演算语言
谓词变元的基本对象是域变量;
代表:QBE;
- 元组关系演算语言
- 具有关系代数和关系演算双重特点的语言;
代表:SQL(Structured Query Language) ;
🕒 3. 关系代数
关系代数运算的三个要素
运算对象:关系
运算结果:关系
运 算 符:四类- 集合运算符
将关系看成元组的集合
运算是从关系的“水平”方向即行的角度来进行 - 专门的关系运算符
不仅涉及行而且涉及列 - 比较运算符
辅助专门的关系运算符进行操作 - 逻辑运算符
辅助专门的关系运算符进行操作

🕘 3.1 传统的集合运算
🕤 符号引入
-
R , t ∈ R , t [ A i ] R,t∈R,t[A_i] R,t∈R,t[Ai]
设关系模式为 R ( A 1 , A 2 , … , A n ) R(A_1,A_2,…,A_n) R(A1,A2,…,An)
它的一个关系设为 R R R
t ∈ R t∈R t∈R表示 t t t是 R R R的一个元组
t [ A i ] t[A_i] t[Ai]则表示元组t中相应于属性 A i A_i Ai的一个分量 -
A A A, t [ A ] t[A] t[A], A ˉ \bar{A} Aˉ
若 A = { A i 1 , A i 2 , … , A i k } A=\left\{Ai1,Ai2,…,Aik\right\} A={Ai1,Ai2,…,Aik}其中 A i 1 , A i 2 , . . . , A i k A_{i1} , A_{i2} , ... ,A_{ik} Ai1,Ai2,...,Aik 是 A 1 , A 2 , . . . , A n A_{1} , A_{2} , ... ,A_{n} A1,A2,...,An中的一部分,则A称为属性列或属性组。Ai1,Ai2,…,Aik
A ˉ \bar{A} Aˉ则表示{ A 1 , A 2 , . . . , A n A_{1} , A_{2} , ... ,A_{n} A1,A2,...,An}中去掉 A i 1 , A i 2 , . . . , A i k A_{i1} , A_{i2} , ... ,A_{ik} Ai1,Ai2,...,Aik后剩余的属性组。
t [ A ] = ( t [ A i 1 ] , t [ A i 2 ] , … , t [ A i k ] ) t[A]=\left(t\left[A_{i 1}\right], \quad t\left[A_{i 2}\right], \ldots, t\left[A_{i k}\right]\right) t[A]=(t[Ai1],t[Ai2],…,t[Aik])表示元组 t t t在属性列 A A A上诸分量的集合。 -
⌢ \frown ⌢
t r t s t_r t_s trts
R为n目关系, S为m目关系。
t r ∈ R , t s ∈ S t_{\mathrm{r}} \in R, t_{\mathrm{s}} \in S tr∈R,ts∈S,
⌢ \frown ⌢
t r t s t_r t_s trts称为元组的连接或者连串。
⌢ \frown ⌢
t r t s t_r t_s trts是一个 n+m 列的元组, 前 n 个分量为 R 中的
一个 n 元组, 后 m 个分量为 S 中的一个 m 元组。 -
象集(images set) Z x Z_x Zx
给定一个关系 R ( X , Z ) R(X,Z) R(X,Z), X X X和 Z Z Z为属性组
当 t [ X ] = x t[X]=x t[X]=x时,x在R中的象集为: Z x = { t [ Z ] ∣ t ∈ R , t [ X ] = x } Z_{\mathrm{x}}=\{t[Z] \mid t \in R, \quad t[X]=x\} Zx={t[Z]∣t∈R,t[X]=x}
它表示 R R R中属性组 X X X上值为 x x x的诸元组在 Z Z Z上分量的集合
例子:
R
x 1 Z 1 x 1 Z 2 x 1 Z 3 x 2 Z 2 x 2 Z 3 x 3 Z 1 x 3 Z 3 x1Z1x1Z2x1Z3x2Z2x2Z3x3Z1x3Z3x1x1x1x2x2x3x3Z1Z2Z3Z2Z3Z1Z3x1x1x1x2x2x3x3Z1Z2Z3Z2Z3Z1Z3 -
x
1
x_1
x1在R中的象集
z x 1 z_{x1} zx1={Z1,Z2,Z3} -
x
2
x_2
x2在R中的象集
z x 2 z_{x2} zx2={Z2,Z3} -
x
3
x_3
x3在R中的象集
z x 3 z_{x3} zx3={Z1,Z3}
并交差运算有什么条件?任意两个集合都可以做这三类集合运算吗?
答: R R R和 S S S(相容的)
- 具有相同的目 n n n(即两个关系都有 n n n个属性)
- 相应的属性取自同一个域
假定给定的两个关系R和S,分别表示学生参加学校社团的轩辕棋社和体育选修课匹克球的学生信息,如图所示

🕤 3.1.1 并(Union)
仍为 n n n目关系,由属于 R R R或属于 S S S的元组组成
R ∪ S = { t ∣ t ∈ R ∨ t ∈ S } R \cup S = \{t \mid t \in R \vee t \in S\} R∪S={t∣t∈R∨t∈S}
其中 t t t为元组变量🕤 3.1.2 差(difference)
仍为 n n n目关系,由属于 R R R而不属于 S S S的所有元组组成
R − S = { t ∣ t ∈ R ∧ t ∉ S } R-S=\{t \mid t \in R \wedge t \notin S\} R−S={t∣t∈R∧t∈/S}🕤 3.1.3 交(intersection)
仍为 n n n目关系,由既属于 R R R又属于 S S S的元组组成
R ∩ S = { t ∣ t ∈ R ∧ t ∈ S } R \cap S=\{t \mid t \in R \wedge t \in S\} R∩S={t∣t∈R∧t∈S}
R ∩ S = R − ( R − S ) R \cap S=R-(R-S) R∩S=R−(R−S)
🕤 3.1.4 笛卡尔积(cartesian product)
严格地讲应该是广义的笛卡尔积(Extended Cartesian Product)
R: r目关系,k1个元组
S: s目关系,k2个元组
R×S- 列:(r+s)列元组的集合
元组的前r列是关系R的一个元组
后s列是关系S的一个元组 - 行: k 1 × k 2 k_1×k_2 k1×k2个元组
-
⌢
\hspace{1.6cm} \frown
⌢
R × S = { t r t s ∣ t r ∈ R ∧ t s ∈ S } R \times S=\left\{t_{\mathrm{r}} t_{\mathrm{s}} \mid t_{\mathrm{r}} \in R \wedge t_{\mathrm{s}} \in S\right\} R×S={trts∣tr∈R∧ts∈S}

RXS的笛卡尔积是十二个元组的表
姓名 系 性别 姓名 系 性别 俊杰 行政管理 男 沐宸 视觉传达 男 俊杰 行政管理 男 若汐 园林 女 俊杰 行政管理 男 育锐 网络工程 男 俊杰 行政管理 男 俊杰 行政管理 男 育锐 网络工程 男 沐宸 视觉传达 男 育锐 网络工程 男 若汐 园林 女 育锐 网络工程 男 育锐 网络工程 男 育锐 网络工程 男 俊杰 行政管理 男 子涵 英语 女 沐宸 视觉传达 男 子涵 英语 女 若汐 园林 女 子涵 英语 女 育锐 网络工程 男 子涵 英语 女 俊杰 行政管理 男 姓名 系 性别 姓名 系 性别 俊杰 行政管理 男 沐宸 视觉传达 男 俊杰 行政管理 男 若汐 园林 女 俊杰 行政管理 男 育锐 网络工程 男 俊杰 行政管理 男 俊杰 行政管理 男 育锐 网络工程 男 沐宸 视觉传达 男 育锐 网络工程 男 若汐 园林 女 育锐 网络工程 男 育锐 网络工程 男 育锐 网络工程 男 俊杰 行政管理 男 子涵 英语 女 沐宸 视觉传达 男 子涵 英语 女 若汐 园林 女 子涵 英语 女 育锐 网络工程 男 子涵 英语 女 俊杰 行政管理 男姓名 俊杰 俊杰 俊杰 俊杰 育锐 育锐 育锐 育锐 子涵 子涵 子涵 子涵 系 行政管理 行政管理 行政管理 行政管理 网络工程 网络工程 网络工程 网络工程 英语 英语 英语 英语 性别 男 男 男 男 男 男 男 男 女 女 女 女 姓名 沐宸 若汐 育锐 俊杰 沐宸 若汐 育锐 俊杰 沐宸 若汐 育锐 俊杰 系 视觉传达 园林 网络工程 行政管理 视觉传达 园林 网络工程 行政管理 视觉传达 园林 网络工程 行政管理 性别 男 女 男 男 男 女 男 男 男 女 男 男 姓名 俊杰 俊杰 俊杰 俊杰 育锐 育锐 育锐 育锐 子涵 子涵 子涵 子涵 系 行政管理 行政管理 行政管理 行政管理 网络工程 网络工程 网络工程 网络工程 英语 英语 英语 英语 性别 男 男 男 男 男 男 男 男 女 女 女 女 姓名 沐宸 若汐 育锐 俊杰 沐宸 若汐 育锐 俊杰 沐宸 若汐 育锐 俊杰 系 视觉传达 园林 网络工程 行政管理 视觉传达 园林 网络工程 行政管理 视觉传达 园林 网络工程 行政管理 性别 男 女 男 男 男 女 男 男 男 女 男 男 
广义的笛卡尔积运算可用于两个关系的连接操作
🕘 3.2 专门的关系运算
假设有教学管理信息系统数据库,该数据库包括有学生关系Student、课程关系Course和选课关系SC。
STUDENT表
Sno Sname Ssex Sage Smajor Shometown 20160101 徐成波 男 20 计算机科学与技术 广东广州 20160102 黄晓君 女 18 计算机科学与技术 湖南衡阳 20160103 林宇珊 女 19 计算机科学与技术 河南新乡 20160104 张茜 女 18 计算机科学与技术 广东中山 20160201 黄晓君 男 21 软件工程 河北保定 20160202 陈金燕 女 19 软件工程 江苏徐州 20160203 张顺峰 男 22 软件工程 河南洛阳 20160204 洪铭勇 男 20 软件工程 河北邯郸 20160301 朱伟东 男 19 网络工程 山东青岛 20160302 叶剑峰 男 20 网络工程 陕西西安 20160303 林宇珊 女 21 网络工程 湖北襄阳 20160304 吴妍娴 女 20 网络工程 浙江诸暨 Sno Sname Ssex Sage Smajor Shometown 20160101 徐成波 男 20 计算机科学与技术 广东广州 20160102 黄晓君 女 18 计算机科学与技术 湖南衡阳 20160103 林宇珊 女 19 计算机科学与技术 河南新乡 20160104 张茜 女 18 计算机科学与技术 广东中山 20160201 黄晓君 男 21 软件工程 河北保定 20160202 陈金燕 女 19 软件工程 江苏徐州 20160203 张顺峰 男 22 软件工程 河南洛阳 20160204 洪铭勇 男 20 软件工程 河北邯郸 20160301 朱伟东 男 19 网络工程 山东青岛 20160302 叶剑峰 男 20 网络工程 陕西西安 20160303 林宇珊 女 21 网络工程 湖北襄阳 20160304 吴妍娴 女 20 网络工程 浙江诸暨Sno 201601012016010220160103201601042016020120160202201602032016020420160301201603022016030320160304 Sname 徐成波 黄晓君 林宇珊 张茜 黄晓君 陈金燕 张顺峰 洪铭勇 朱伟东 叶剑峰 林宇珊 吴妍娴 Ssex 男 女 女 女 男 女 男 男 男 男 女 女 Sage 201819182119222019202120 Smajor 计算机科学与技术 计算机科学与技术 计算机科学与技术 计算机科学与技术 软件工程 软件工程 软件工程 软件工程 网络工程 网络工程 网络工程 网络工程 Shometown 广东广州 湖南衡阳 河南新乡 广东中山 河北保定 江苏徐州 河南洛阳 河北邯郸 山东青岛 陕西西安 湖北襄阳 浙江诸暨 Sno 201601012016010220160103201601042016020120160202201602032016020420160301201603022016030320160304 Sname 徐成波 黄晓君 林宇珊 张茜 黄晓君 陈金燕 张顺峰 洪铭勇 朱伟东 叶剑峰 林宇珊 吴妍娴 Ssex 男 女 女 女 男 女 男 男 男 男 女 女 Sage 201819182119222019202120 Smajor 计算机科学与技术 计算机科学与技术 计算机科学与技术 计算机科学与技术 软件工程 软件工程 软件工程 软件工程 网络工程 网络工程 网络工程 网络工程 Shometown 广东广州 湖南衡阳 河南新乡 广东中山 河北保定 江苏徐州 河南洛阳 河北邯郸 山东青岛 陕西西安 湖北襄阳 浙江诸暨 COURSE表
Cno Cname Cpno Ccredit 1001 高等数学 9.0 1002 C语言程序设计 3.5 1003 数据结构 1002 4.0 1004 操作系统 1003 4.0 1005 数据库原理及应用 1003 3.5 1006 信息管理系统 1005 3.0 1007 面向对象与程序设计 1002 3.5 1008 数据挖掘 1006 3.0 Cno Cname Cpno Ccredit 1001 高等数学 9.01002 C语言程序设计 3.51003 数据结构 10024.01004 操作系统 10034.01005 数据库原理及应用 10033.51006 信息管理系统 10053.01007 面向对象与程序设计 10023.51008 数据挖掘 10063.0Cno 10011002100310041005100610071008 Cname 高等数学 C语言程序设计 数据结构 操作系统 数据库原理及应用 信息管理系统 面向对象与程序设计 数据挖掘 Cpno 100210031003100510021006 Ccredit 9.03.54.04.03.53.03.53.0SC表
Sno Cno Grade 20160101 1001 92 20160101 1002 98 20160101 1003 88 20160101 1004 98 20160101 1005 76 20160101 1006 89 20160101 1007 86 20160101 1008 90 20160102 1005 80 20160201 1005 90 20160203 1003 89 20160204 1005 96 20160303 1001 88 20160303 1002 86 20160303 1003 68 20160303 1004 98 20160303 1005 84 20160303 1006 73 Sno Cno Grade 201601011001922016010110029820160101100388201601011004982016010110057620160101100689201601011007862016010110089020160102100580201602011005902016020310038920160204100596201603031001882016030310028620160303100368201603031004982016030310058420160303100673Sno 201601012016010120160101201601012016010120160101201601012016010120160102201602012016020320160204201603032016030320160303201603032016030320160303 Cno 100110021003100410051006100710081005100510031005100110021003100410051006 Grade 929888987689869080908996888668988473🕤 3.2.1 选择(selection)
- 选择又称为限制(Restriction)
- 选择运算符的含义
- 在关系 R R R中选择满足给定条件的诸元组
- σ F ( R ) = { t ∣ t ∈ R ∧ F ( t ) = ′ true ′ } \sigma_{\mathrm{F}}(R)=\left\{t \mid t \in R \wedge F(t)={ }^{\prime} \operatorname{true}^{\prime}\right\} σF(R)={t∣t∈R∧F(t)=′true′}
- F:选择条件,是一个逻辑表达式
基本形式为: X 1 θ Y 1 X_1θY_1 X1θY1
θ表示比较运算符,它可以是>,≥,<,≤,=或 ≠。
- 选择运算是从关系R中选取使逻辑表达式F为真的元组,是从行的角度进行的运

例题:
从student关系中查询女同学的情况,和年龄在19岁及其以下的软件工程专业的学生-
σ
Ssex
=
“女”
(
Student
)
\sigma_{\text {Ssex } = \text { “女” }}(\text { Student })
σSsex = “女” ( Student )或
σ
3
=
“女”
(
Student
)
\sigma_{\text {3 } = \text { “女” }}(\text { Student })
σ3 = “女” ( Student )
Sno Sname Ssex Sage Smajor Shometown 20160102 黄晓君 女 18 计算机科学与技术 湖南衡阳 20160103 林宇珊 女 19 计算机科学与技术 河南新乡 20160104 张茜 女 18 计算机科学与技术 广东中山 20160202 陈金燕 女 19 软件工程 江苏徐州 20160303 林宇珊 女 21 网络工程 湖北襄阳 20160304 吴妍娴 女 20 网络工程 浙江诸暨 Sno Sname Ssex Sage Smajor Shometown 20160102 黄晓君 女 18 计算机科学与技术 湖南衡阳 20160103 林宇珊 女 19 计算机科学与技术 河南新乡 20160104 张茜 女 18 计算机科学与技术 广东中山 20160202 陈金燕 女 19 软件工程 江苏徐州 20160303 林宇珊 女 21 网络工程 湖北襄阳 20160304 吴妍娴 女 20 网络工程 浙江诸暨Sno 201601022016010320160104201602022016030320160304 Sname 黄晓君 林宇珊 张茜 陈金燕 林宇珊 吴妍娴 Ssex 女 女 女 女 女 女 Sage 181918192120 Smajor 计算机科学与技术 计算机科学与技术 计算机科学与技术 软件工程 网络工程 网络工程 Shometown 湖南衡阳 河南新乡 广东中山 江苏徐州 湖北襄阳 浙江诸暨 -
σ
Sage
<
=
19
∧
Smajor
=
’软件工程’
(
Student
)
\sigma_{\text {Sage }<=19 \wedge \text { Smajor }=\text { '软件工程' }}(\text { Student })
σSage <=19∧ Smajor = ’软件工程’ ( Student )
Sno Sname Ssex Sage Smajor Shometown 20160202 陈金燕 女 19 软件工程 江苏徐州 Sno Sname Ssex Sage Smajor Shometown 20160202 陈金燕 女 19 软件工程 江苏徐州Sno 20160202 Sname 陈金燕 Ssex 女 Sage 19 Smajor 软件工程 Shometown 江苏徐州
🕤 3.2.2 投影(project)
-
含义:从R中选择出若干属性列组成新的关系
π A ( R ) = { t [ A ] ∣ t ∈ R } \pi_{A}(R)=\{t[A] \mid t \in R\} πA(R)={t[A]∣t∈R}
A:R中的属性列 -
投影操作主要是从列的角度进行运算

但投影之后不仅取消了原关系中的某些列,而且还可能取消某些元组(避免重复行)
例:查询全部课程的课程名和学分
Π Cname, Ccredit ( Course) 或 Π 2 , 4 ( Course ) \Pi_{\text {Cname, Ccredit }}\left(\text { Course) 或 } \mathrm{\Pi}_{2,4}(\text { Course })\right. ΠCname, Ccredit ( Course) 或 Π2,4( Course )
Cname Ccredit 高等数学 9.0 C语言程序设计 3.5 数据结构 4.0 操作系统 4.0 数据库原理及应用 3.5 信息管理系统 3.0 面向对象与程序设计 3.5 数据挖掘 3.0 \text { Cname } Ccredit 高等数学 9.0 C语言程序设计 3.5 数据结构 4.0 操作系统 4.0 数据库原理及应用 3.5 信息管理系统 3.0 面向对象与程序设计 3.5 数据挖掘 3.0
Cname 高等数学 C语言程序设计 数据结构 操作系统 数据库原理及应用 信息管理系统 面向对象与程序设计 数据挖掘 Ccredit 9.03.54.04.03.53.03.53.0🕤 3.2.3 连接(join)
连接也称为θ连接,
从两个关系的笛卡尔积中选取属性间满足一定条件的元组(A和B:分别为R和S上度(列)数相等且可比的属性组,θ是比较运算符)

即:找出R×S中满足R中属性组A的值与S中的属性组B的值满足比较关系θ的那些元组。
-
等值连接: 当θ取“=”时为等值连接

等值连接的具体计算过程如下:
①计算R×S;
②找出R×S中满足R中属性组A的值与S中的属性组B的值相等的那些元组。
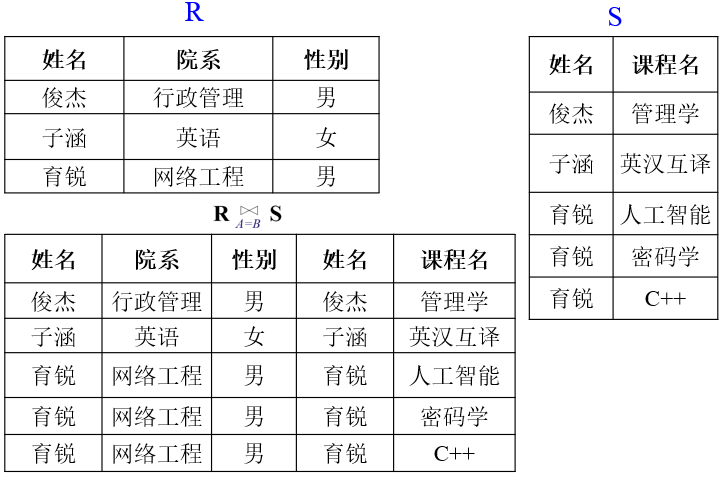
-
自然连接

两个关系中进行比较的分量必须是相同的属性组,在结果中把重复的属性列去掉
自然连接的计算过程如下:
① 计算R×S;
② 设R和S的公共属性是B,则找出R×S中满足R中属性B的值与S中的属性B的值相等的那些元组;
③ 去掉重复的属性列,如可去掉S中的B列保留R中B列。

笛卡尔积:16个元组(姓名,住址,姓名,工作单位,工资)
连接:三个元组- 一般的连接操作是从行的角度进行运算。

自然连接还需要取消重复列,所以是同时从行和列的角度进行运算。
例题:关系R和关系S如下所示
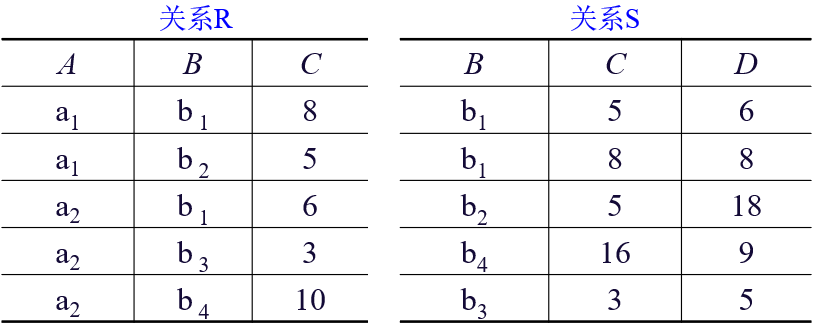

等值连接和自然连接的比较
- 自然连接一定是等值连接,但等值连接不一定是自然连接;
- 等值连接要求有值相等的属性列,但不一定具有相同的属性名,而自然连接要求相等属性值的属性名必须相同;
- 等值连接不做投影运算,而自然连接要把重复的属性列去掉。
例题:查询学生选修课程的信息,包括学生的学号、姓名、性别、课程名、学分和成绩。
答案: Π Sno, Sname, Ssex, Cname, Ccredi, Grade ( Student ⋈ S C ⋈ C o u r s e ) \Pi_{\text {Sno, Sname, Ssex, Cname, Ccredi, Grade }}\left(\text {Student} \bowtie \mathbf{SC} \bowtie \mathbf{Course}\right) ΠSno, Sname, Ssex, Cname, Ccredi, Grade (Student⋈SC⋈Course)❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页🕞 3.2.3.1 (左/右)外连接

外连接- 在作自然连接时,如果把舍弃的元组也保存在结果关系中,而在其他属性上填空值(Null),这种连接就叫做外连接(outer join)。
姓名 住址 工作单位 工资 俊杰 北京朝阳 清华附小 11500 子涵 上海 新东方 9500 育锐 广州 仲恺农大 8500 沐宸 西安 NULL NULL 奕辰 NULL 小米公司 15000 姓名 住址 工作单位 工资 俊杰 北京朝阳 清华附小 11500 子涵 上海 新东方 9500 育锐 广州 仲恺农大 8500 沐宸 西安 NULL NULL 奕辰 NULL 小米公司 15000姓名 俊杰 子涵 育锐 沐宸 奕辰 住址 北京朝阳 上海 广州 西安 NULL 工作单位 清华附小 新东方 仲恺农大 NULL 小米公司 工资 1150095008500 NULL 15000
左外连接
- 如果只把左边关系R中要舍弃的元组保留就叫做左外连接(left outer join或left join)
姓名 住址 工作单位 工资 俊杰 北京朝阳 清华附小 11500 子涵 上海 新东方 9500 育锐 广州 仲恺农大 8500 沐宸 西安 NULL NULL 姓名 住址 工作单位 工资 俊杰 北京朝阳 清华附小 11500 子涵 上海 新东方 9500 育锐 广州 仲恺农大 8500 沐宸 西安 NULL NULL姓名 俊杰 子涵 育锐 沐宸 住址 北京朝阳 上海 广州 西安 工作单位 清华附小 新东方 仲恺农大 NULL 工资 1150095008500 NULL
右外连接
- 如果只把右边关系S中要舍弃的元组保留就叫做右外连接(right outer join或right join)。
姓名 住址 工作单位 工资 俊杰 北京朝阳 清华附小 11500 子涵 上海 新东方 9500 育锐 广州 仲恺农大 8500 奕辰 NULL 小米公司 15000 姓名 住址 工作单位 工资 俊杰 北京朝阳 清华附小 11500 子涵 上海 新东方 9500 育锐 广州 仲恺农大 8500 奕辰 NULL 小米公司 15000姓名 俊杰 子涵 育锐 奕辰 住址 北京朝阳 上海 广州 NULL 工作单位 清华附小 新东方 仲恺农大 小米公司 工资 1150095008500 15000
🕤 3.2.4 除(division)
给定关系 R ( X , Y ) R (X,Y) R(X,Y)和 S ( Y , Z ) S (Y,Z) S(Y,Z),其中 X , Y , Z X,Y,Z X,Y,Z为属性组。
R R R中的 Y Y Y与 S S S中的 Y Y Y可以有不同的属性名,但必须出自相同的域集。
R R R与 S S S的除运算得到一个新的关系 P ( X ) P(X) P(X),为:
R ÷ S = { t r [ X ] ∣ t r ∈ R ∧ Π Y ( S ) ⊆ Y x } R \div S=\left\{t_{\mathrm{r}}[X] \mid t_{\mathrm{r}} \in R \wedge \Pi_{\mathrm{Y}}(S) \subseteq Y_{x}\right\} R÷S={tr[X]∣tr∈R∧ΠY(S)⊆Yx}
Y x Y_x Yx: x x x在 R R R中的象集, x = t r [ X ] x = t_r[X] x=tr[X]
含义: P P P是R中满足下列条件的元组在 X 属性列上的投影:
元组在X上分量值x的象集Yx包含S在Y上投影的集合。
除操作是同时从行和列角度进行运算
例1:试找出修读了全部课程的学生的学号。
对这个问题可用除法解决,即S_C÷C
分析过程:对于关系S_C,Sno可以取三个值{S1,S2,S3},其中
S1的象集的含义是学生S1上的课程,即: C n o S 1 Cno_{S1} CnoS1= { c1,c2 ,c3};
S2的象集 C n o S 2 Cno_{S2} CnoS2= { c2 ,c3};S3的象集 C n o S 3 Cno_{S3} CnoS3= { c2};
C在Cno上的投影代表所有课程,即: Π c n o Π_{cno} Πcno ( C )={ c1,c2,c3},
只有S1这位同学上了全部课程,即:只有S1的象集包含了C在Cno属性组上的投影,所以S_C÷C={S1}
思考:至少选修了1号和2号课程的学生的学号
即S_C÷K
其中K:
例2:设关系R、S分别为下图的(a)和(b),R÷S的结果为图©
分析:在关系R中,A可以取三个值{a1,a2,a3}
a1的象集为 {(b1,5),(b2,6),(b3,12)};
a2的象集为 {(b1,5),(b3,12)}; a3的象集为 {(b3,12)}
S在(B,C)上的投影为{(b1,5),(b2,6),(b3,12)}
只有a1的象集包含了S在(B,C)属性组上的投影,所以R÷S ={a1}。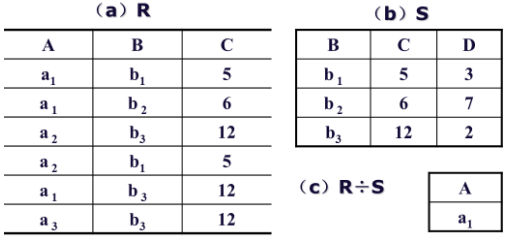
例3:
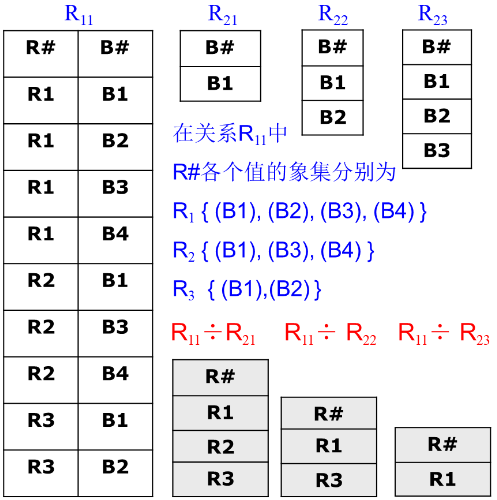
🕘 3.3 关系代数综合举例
假设有教学管理信息系统数据库,该数据库包括有学生关系Student、课程关系Course和选课关系SC。
STUDENT表
Sno Sname Ssex Sage Smajor Shometown 20160101 徐成波 男 20 计算机科学与技术 广东广州 20160102 黄晓君 女 18 计算机科学与技术 湖南衡阳 20160103 林宇珊 女 19 计算机科学与技术 河南新乡 20160104 张茜 女 18 计算机科学与技术 广东中山 20160201 黄晓君 男 21 软件工程 河北保定 20160202 陈金燕 女 19 软件工程 江苏徐州 20160203 张顺峰 男 22 软件工程 河南洛阳 20160204 洪铭勇 男 20 软件工程 河北邯郸 20160301 朱伟东 男 19 网络工程 山东青岛 20160302 叶剑峰 男 20 网络工程 陕西西安 20160303 林宇珊 女 21 网络工程 湖北襄阳 20160304 吴妍娴 女 20 网络工程 浙江诸暨 Sno Sname Ssex Sage Smajor Shometown 20160101 徐成波 男 20 计算机科学与技术 广东广州 20160102 黄晓君 女 18 计算机科学与技术 湖南衡阳 20160103 林宇珊 女 19 计算机科学与技术 河南新乡 20160104 张茜 女 18 计算机科学与技术 广东中山 20160201 黄晓君 男 21 软件工程 河北保定 20160202 陈金燕 女 19 软件工程 江苏徐州 20160203 张顺峰 男 22 软件工程 河南洛阳 20160204 洪铭勇 男 20 软件工程 河北邯郸 20160301 朱伟东 男 19 网络工程 山东青岛 20160302 叶剑峰 男 20 网络工程 陕西西安 20160303 林宇珊 女 21 网络工程 湖北襄阳 20160304 吴妍娴 女 20 网络工程 浙江诸暨Sno 201601012016010220160103201601042016020120160202201602032016020420160301201603022016030320160304 Sname 徐成波 黄晓君 林宇珊 张茜 黄晓君 陈金燕 张顺峰 洪铭勇 朱伟东 叶剑峰 林宇珊 吴妍娴 Ssex 男 女 女 女 男 女 男 男 男 男 女 女 Sage 201819182119222019202120 Smajor 计算机科学与技术 计算机科学与技术 计算机科学与技术 计算机科学与技术 软件工程 软件工程 软件工程 软件工程 网络工程 网络工程 网络工程 网络工程 Shometown 广东广州 湖南衡阳 河南新乡 广东中山 河北保定 江苏徐州 河南洛阳 河北邯郸 山东青岛 陕西西安 湖北襄阳 浙江诸暨 COURSE表
Cno Cname Cpno Ccredit 1001 高等数学 9.0 1002 C语言程序设计 3.5 1003 数据结构 1002 4.0 1004 操作系统 1003 4.0 1005 数据库原理及应用 1003 3.5 1006 信息管理系统 1005 3.0 1007 面向对象与程序设计 1002 3.5 1008 数据挖掘 1006 3.0 Cno Cname Cpno Ccredit 1001 高等数学 9.01002 C语言程序设计 3.51003 数据结构 10024.01004 操作系统 10034.01005 数据库原理及应用 10033.51006 信息管理系统 10053.01007 面向对象与程序设计 10023.51008 数据挖掘 10063.0Cno 10011002100310041005100610071008 Cname 高等数学 C语言程序设计 数据结构 操作系统 数据库原理及应用 信息管理系统 面向对象与程序设计 数据挖掘 Cpno 100210031003100510021006 Ccredit 9.03.54.04.03.53.03.53.0SC表
Sno Cno Grade 20160101 1001 92 20160101 1002 98 20160101 1003 88 20160101 1004 98 20160101 1005 76 20160101 1006 89 20160101 1007 86 20160101 1008 90 20160102 1005 80 20160201 1005 90 20160203 1003 89 20160204 1005 96 20160303 1001 88 20160303 1002 86 20160303 1003 68 20160303 1004 98 20160303 1005 84 20160303 1006 73 Sno Cno Grade 201601011001922016010110029820160101100388201601011004982016010110057620160101100689201601011007862016010110089020160102100580201602011005902016020310038920160204100596201603031001882016030310028620160303100368201603031004982016030310058420160303100673Sno 201601012016010120160101201601012016010120160101201601012016010120160102201602012016020320160204201603032016030320160303201603032016030320160303 Cno 100110021003100410051006100710081005100510031005100110021003100410051006 Grade 929888987689869080908996888668988473例1:查询计算机科学与技术专业选修了2号课程的学生的姓名和成绩。
Π Sname, Grade ( σ C n o = ′ 2 ′ ∧ S m a j o r = " 计算机科学与技术 " ( Student ⋈ S C ) ) \Pi_{\text {Sname, Grade }}\left(\sigma_{\mathbf{C n o}={ }^{\prime} 2^{\prime}} \wedge _{Smajor="计算机科学与技术"}(\text { Student} \bowtie \mathbf{SC})\right) ΠSname, Grade (σCno=′2′∧Smajor="计算机科学与技术"( Student⋈SC))例2:查询选修了学分在3分及以上的课程的学生的学号、姓名及所选修课程的课程名和成绩。
Π Sno, Sname, Cname, Grade ( σ C r e d i t > = 3 ( Student ⋈ S C ⋈ C o u r s e ) ) \Pi_{\text {Sno, Sname, Cname, Grade }}\left(\sigma_{\mathbf{Credit}>=3} (\text { Student} \bowtie \mathbf{SC} \bowtie \mathbf{Course})\right) ΠSno, Sname, Cname, Grade (σCredit>=3( Student⋈SC⋈Course))例3:查询选修了全部课程的学生的学号和姓名。
( Π Sno,Cno ( S C ) ÷ Π Cno (Course) ) ⋈ Π Sno,Sname (Student) \left(\Pi_{\text {Sno,Cno }}(\mathbf{S C}) \div \Pi_{\text {Cno }} \text { (Course) }\right) \bowtie \Pi_{\text {Sno,Sname }} \text { (Student) } (ΠSno,Cno (SC)÷ΠCno (Course) )⋈ΠSno,Sname (Student)例4:查询选修了其直接先行课为1号课程的学生姓名
三种表示
Π Sname ( σ C p n o = ′ 1 ′ ( Course ⋈ S C ⋈ S t u d e n t ) ) Π Sname ( σ Cpno=’1’ ( Course ) ⋈ S C ⋈ Π Sno, name ( Student ) ) Π Sname ( Π Sno ( σ Cpno=’1’ ( Course ) ⋈ S C ) ⋈ Π Sno, Sname ( Student ) ) ΠSname (σCpno=′1′(Course ⋈SC⋈Student))ΠSname (σCpno='1' (Course )⋈SC⋈ΠSno, name ( Student ))ΠSname (ΠSno (σCpno='1' ( Course )⋈SC)⋈ΠSno, Sname ( Student ))ΠSname (σCpno=′1′(Course ⋈SC⋈Student))ΠSname (σCpno=’1’ (Course )⋈SC⋈ΠSno, name ( Student ))ΠSname (ΠSno (σCpno=’1’ ( Course )⋈SC)⋈ΠSno, Sname ( Student ))🕘 3.4 关系代数小结
-
关系代数运算
- 关系代数运算
并、差、交、笛卡尔积、投影、选择、连接、除 - 基本运算
并、差、笛卡尔积、投影、选择 - 交、连接、除
可以用5种基本运算来表达
- 关系代数运算
-
关系代数表达式
关系代数运算经有限次复合后形成的式子 -
典型关系代数语言
ISBL(Information System Base Language)
由IBM United Kingdom研究中心研制
用于PRTV(Peterlee Relational Test Vehicle)实验系统
🕒 4. 课后习题
-
【单选题】现有一个关系:借阅(书号、书名,库存数,读者号,借期,还期),假如同一本书允许一个读者多次借阅,但不能同时对一种书借多本。则该关系模式的码是( )。
A、书号
B、读者号
C、书号+读者号
D、书号+读者号+借期 -
【单选题】有关系 :R(A, B, C) 主码=A,S(D,A) 主码=D,外码=A,参照于R的属性A
关系R和S的元组如下图所示:

指出关系S中违反关系完整性规则的元组是( )
A、(1,2)
B、 (2, null)
C、(3,3)
D、(4,1) -
【判断题】一个关系中不可能出现两个完全相同的元组是由实体完整性规则确定的( )
-
【判断题】有两个关系R、S,都含有A属性,关系R中的属性A是主码,关系S中属性A是外码,那么关系R、S中属性A的域可以不同( )。
-
【单选题】设有关系R(A,B,C)和关系S(B,C,D),那么与R⋈S等价的关系代数表达式是( )
A、 π 1 , 2 , 3 , 4 ( σ 2 = 1 ∧ 3 = 2 ( R × S )) π_{1,2,3,4}(σ_{2=1∧3=2}(R×S)) π1,2,3,4(σ2=1∧3=2(R×S))
B、 π 1 , 2 , 3 , 6 ( σ 2 = 1 ∧ 3 = 2 ( R × S )) π_{1,2,3,6}(σ_{2=1∧3=2}(R×S)) π1,2,3,6(σ2=1∧3=2(R×S))
C、 π 1 , 2 , 3 , 6 ( σ 2 = 4 ∧ 3 = 5 ( R × S )) π_{1,2,3,6}(σ_{2=4∧3=5}(R×S)) π1,2,3,6(σ2=4∧3=5(R×S))
D、 π 1 , 2 , 3 , 4 ( σ 2 = 4 ∧ 3 = 5 ( R × S )) π_{1,2,3,4}(σ_{2=4∧3=5}(R×S)) π1,2,3,4(σ2=4∧3=5(R×S)) -
【单选题】设W=R⋈S,且W、R、S的属性个数分别为w、r和s,那么三者之间应满足( )
A、w ≤ r+s
B、w<r+s
C、w ≥ r+s
D、w>r+s -
设关系R与关系S具有相同的目(或称度),且相对应的属性的值取自同一个域,则 R − ( R − S ) R-(R-S) R−(R−S)等于( )
A、 R ∪ S R ∪ S R∪S
B、 R ∩ S R ∩ S R∩S
C、 R × S R × S R×S
D、 R − S R - S R−S -
【填空题】在关系代数的专门关系运算中,从表中取出满足条件的属性的操作称为______;从表中选出满足某种条件的元组的操作称为_______;将两个关系中具有共同属性值的元组连接到一起构成新表的操作称为________。
-
【单选题】在关系代数的传统集合运算中,假定有关系R和S,运算结果为W,如果W中的元组属于R,或者属于S,则W的运算的结果是
A、笛卡尔积
B、并
C、差
D、交 -
【单选题】关系运算中花费时间可能最长的运算是( )
A、投影
B、选择
C、笛卡尔积
D、除 -
【单选题】等值连接和自然连接相比较,正确的是( )。
A、等值连接和自然连接的结果完全相同
B、等值连接的属性个数大于自然连接的属性个数
C、等值连接的属性个数大于或等于自然连接的属性个数
D、等值连接和自然连接的连接条件相同 -
【单选题】参加差运算的两个关系( ).
A、属性个数可以不相同
B、属性个数必须相同
C、一个关系包含另一个关系的属性
D、属性名必须相同 -
【单选题】有两个关系R和S,分别包含15个和10个元组,则在RUS、R-S、RnS中不可能出现的元组数目情况是( )。
A、15,5,10
B、18,7,7
C、21,11,4
D、25,15,0 -
【单选题】在n元关系R中,公式 σ 3 < “ 4 ” ( R ) σ_{3<“4”}(R) σ3<“4”(R)表示( )。
A、从R中选择值为3的分量(或属性)小于第4个分量值的元组组成的关系
B、从R中选择第3个分量的值小于第4个分量值的元组组成的关系
C、从R中选择第3个分量的值小于4的元组组成的关系
D、从R中选择第3个分量小于4个元组组成的关系 -
【判断题】给定关系R(X,Y)和S(Y,Z),R和S作除运算时要求R中的属性Y和S中的属性Y必须具有相同的域()
-
【单选题】设关系 R ( A , B , C ) R(A,B,C) R(A,B,C)和 S ( B , C , D ) S(B,C,D) S(B,C,D),下列各关系代数表达式不成立的是()
A、 R ÷ S R ÷ S R÷S
B、 π B , C ( R ) ∪ π B , C ( S ) π_{B,C}(R)∪π_{B,C}(S) πB,C(R)∪πB,C(S)
C、 R ∩ S R ∩ S R∩S
D、 R × S R × S R×S -
设有关系R、S和T,如图所示
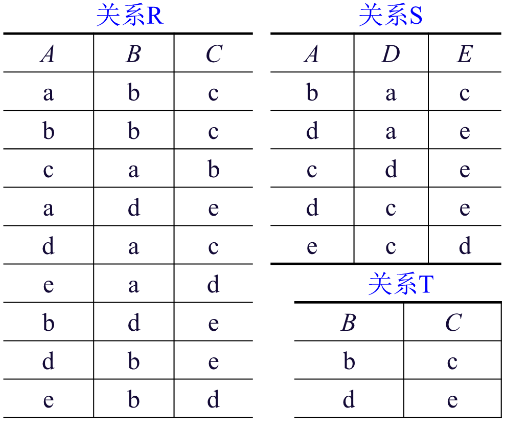
计算: ( 1 ) ∏ 3 , 2 ( S ) ( 2 ) σ B = ′ b ′ a n d C = “ c ” ( R ) ( 3 ) R ⋈ S ( 4 ) Π А,В,C,D ( R ⋈ S ) ( 5 ) R ÷ T (1) \prod_{3,2}(\mathrm{~S}) \\ (2) \sigma_{B='b' and \, C=“c”}(R) \\ (3) R \bowtie S \\ (4) \Pi_{\text {А,В,C,D }}(R \bowtie S) \\ (5) R \div T (1)∏3,2( S)(2)σB=′b′andC=“c”(R)(3)R⋈S(4)ΠА,В,C,D (R⋈S)(5)R÷T
-
设有三个关系
S(SNO,SNAME,AGE,SEX,SDEPT)
SC(SNO,CNO,GRADE)
C(CNO,CNAME,TNAME)
试用关系代数语言完成下列查询:
(1) LIU老师所教授课程的课程号、课程名;
(2) 检索年龄大于23岁的男学生的学号和姓名;
(3) 检索学号为S3的学生所学课程的课程名与任课老师名;
(4) 检索至少选修LIU老师所教授课程中一门课的女学生姓名;
(5) 检索WANG同学不学的课程的课程号;
(6) 检索全部学生都选修的课程的课程号和课程名;
(7) 检索选修课程包含LIU老师所有教授课程的学生学号; -
设有一个SPJ数据库,包括S,P,J,SPJ四个关系模式:
S(SNO,SNAME,STATUS,SCITY);
P(PNO,PNAME,COLOR,WEIGHT);
J(JNO,JNANE,JCITY);
SPJ(SNO,PNO,JNO,QTY)。
其中:供应商表S由供应商代码(SNO)、供应商姓名(SNAME)、供应商状态(STATUS)、供应商所在城市(SCITY)组成;零件表P由零件代码(PNO)、零件名(PNAME)、颜色(COLOR)、重量(WEIGHT)组成;工程项目表J 由工程项目代码(JNO)、工程项目名(JNAME)、工程项目所在城市(JCITY)组成;供应情况表SPJ由供应商代码(SNO)、零件代码(PNO)、工程项目代码(JNO)、供应数量组成(QTY)组成,表示某供应商供应某种零件给某工程项目的数量为QTY。现有具体数据如图所示,a、b、c、d分别代表S表、P表、J表和SPJ表。

试用关系代数完成如下查询:
(1)求供应工程J1 零件的供应商号码SNO;
(2)求供应工程J1 零件P1的供应商号码SNO;
(3)求供应工程J1 零件为红色的供应商号码SNO;
(4)求没有使用天津供应商生产的红色零件的工程号JNO;
(5)求至少用了供应商S1所供应的全部零件的工程号JNO。
答案:1.D 2.C(解析:R中的A只有1、2,没有3,因此S中外码A找不到参照的对应) 3.√ 4.×(解析:根据关系的参照完整性,关系S中的属性A必须引用关系R中的属性A,如果它们的域不同,则可能不存在引用情况。)5.C(解析:标号,R.A(1)、R.B(2)、R.C(3)、S.B(4)、S.C(5)、S.D(6),显然自然连接就是R.B(2)=S.B(4);R.C(3)=S.C(5),所以我们只要投影1、2、3、6或者1、4、5、6即可) 6.B(解析:要去掉重复的属性列) 7.B(解析:画图) 8.投影、选择、连接 9.B 10.C 11.B 12.B(解析:参加差运算的两个关系要求是相容关系,即两个关系属性个数相同,相应的属性值域相同。) 13.B(解析:答案A的情形:若RnS为10个元组,那么RUS为15个元组、R-S为5个元组是正确的;答案B的情形:若RnS为7个元组,那么RUS应为18个元组、R-S应为8个元组;答案C的情形:若RnS为4个元组,那么RUS为21个元组、R-S为11个元组是正确的;答案D的情形:若RnS为0个元组,那么RUS为25个元组、R-S为15个元组是正确的。)14.C(解析:条件表达式3<"4",3表示R的第3个属性,"4"表示值。)15.√ 16.C(解析:有相同属性列,A对;参加并交差运算的两个关系要求是相容关系,即两个关系属性个数相同,相应的属性值域相同,B对;D显然对;而C不满足相容关系的条件,值域不同,错误)
17.答:
(1)
E D c a e a e d e c d c EDcaeaedecdcEceeedDaadcc
(2)
A B C a b c b b c ABCabcbbcAabBbbCcc
(3)
A B C D E b b c a c b d e a c d a c a e d b e a e d a c c e d b e c e c a b d e e a d c d e b d c d ABCDEbbcacbdeacdacaedbeaedaccedbececabdeeadcdebdcdAbbddddceeBbdababaabCcececebddDaaaaccdccEcceeeeedd(4)
A B C D b b c a b d e a d a c a d b e a d a c c d b e c c a b d e a d c e b d c ABCDbbcabdeadacadbeadaccdbeccabdeadcebdcAbbddddceeBbdababaabCcececebddDaaaaccdcc(5)
在关系R中,A可能的取值为{a,b,c,d,e}
a的像集为{(b,c),(d,e)}
b的像集为{(b,c),(d,e)}
c的像集为{(a,b)}
d的像集为{(a,c),(b,e)}
e的像集为{(a,d),(b,d)}
T在(B,C)上的投影为{(b,c),(d,e)}
只有a,b的像集包含了T在(B,C)属性组上的投影,所以R÷T={a,b}。18.答:
(1) Π CNO, CNAME ( σ TNAME = ′ LIU ′ ( C ) ) \Pi_{\text {CNO, CNAME }}\left(\sigma_{\text{TNAME}={ }^{\prime} \text {LIU}^{\prime}} (\text{C})\right) ΠCNO, CNAME (σTNAME=′LIU′(C))
(2) Π SNO, SNAME ( σ AGE > 23 ∧ SEX=’男’ ( S ) ) \Pi_{\text {SNO, SNAME }}\left(\sigma_{\text{AGE}>23}\wedge _{\text{SEX='男'}} (\text{S})\right) ΠSNO, SNAME (σAGE>23∧SEX=’男’(S))
(3) Π CNAME, TNAME ( σ SNO = ′ S3 ′ ( SC ⋈ C ) ) \Pi_{\text {CNAME, TNAME }}\left(\sigma_{\text{SNO}={ }^{\prime} \text {S3}^{\prime}} (\text {SC} \bowtie \text{C})\right) ΠCNAME, TNAME (σSNO=′S3′(SC⋈C))
或
Π CNAME, TNAME ( σ SNO = ′ S3 ′ (SC) ⋈ C ) \Pi_{\text {CNAME, TNAME }}\left(\sigma_{\text{SNO}={ }^{\prime} \text {S3}^{\prime}} \text {(SC)} \bowtie \text{C}\right) ΠCNAME, TNAME (σSNO=′S3′(SC)⋈C)
或
Π CNAME, TNAME ( σ SNO = ′ S3 ′ ∧ SC.CNO=C.CNO ( SC × C ) ) \Pi_{\text {CNAME, TNAME }}\left(\sigma_{\text{SNO}={ }^{\prime} \text {S3}^{\prime}}\wedge _\text{SC.CNO=C.CNO}(\text {SC} \times \text{C})\right) ΠCNAME, TNAME (σSNO=′S3′∧SC.CNO=C.CNO(SC×C))
(4) Π SNAME ( σ SEX = ′ 女 ′ ∧ TNAME=’LIU’ ( S ⋈ SC ⋈ C ) ) \Pi_{\text {SNAME}}\left(\sigma_{\text{SEX}={ }^{\prime} \text {女}^{\prime}} \wedge _\text{TNAME='LIU'}(\text {S} \bowtie \text {SC} \bowtie \text{C})\right) ΠSNAME(σSEX=′女′∧TNAME=’LIU’(S⋈SC⋈C))
或
Π SNAME ( σ SEX = ′ 女 ′ (S) ⋈ SC ⋈ σ TNAME=’LIU’ ( C ) ) \Pi_{\text {SNAME}}\left(\sigma_{\text{SEX}={ }^{\prime} \text {女}^{\prime}} \text {(S)} \bowtie \text {SC} \bowtie \sigma_\text{TNAME='LIU'}( \text{C})\right) ΠSNAME(σSEX=′女′(S)⋈SC⋈σTNAME=’LIU’(C))
(5) Π CNO (C) − Π CNO ( σ SNAME = ′ WANG ′ ( S ⋈ SC ) ) \Pi_{\text {CNO}} \text {(C)} - \Pi_\text {CNO} \left(\sigma_{\text{SNAME}={ }^{\prime} \text {WANG}^{\prime}} (\text {S} \bowtie \text{SC})\right) ΠCNO(C)−ΠCNO(σSNAME=′WANG′(S⋈SC))
或
Π CNO (C) − Π CNO ( σ SNAME = ′ WANG ′ (S) ⋈ SC ) ) \Pi_{\text {CNO}} \text {(C)} - \Pi_\text {CNO} \left(\sigma_{\text{SNAME}={ }^{\prime} \text {WANG}^{\prime}} \text {(S)} \bowtie \text{SC})\right) ΠCNO(C)−ΠCNO(σSNAME=′WANG′(S)⋈SC))
或
Π CNO (C) − Π CNO ( σ SNAME = ′ WANG ′ ∧ S.SNO=SC.SNO ( S × SC ) ) \Pi_{\text {CNO}} \text {(C)} - \Pi_\text {CNO} \left(\sigma_{\text{SNAME}={ }^{\prime} \text {WANG}^{\prime}}\wedge _\text{S.SNO=SC.SNO}(\text {S} \times \text{SC})\right) ΠCNO(C)−ΠCNO(σSNAME=′WANG′∧S.SNO=SC.SNO(S×SC))
(6) Π CNO, CNAME ( C ⋈ ( Π CNO, SNO ( SC ) ÷ Π SNO ( S ) ) ) \Pi_{\text {CNO, CNAME }}\left(\text{C} \bowtie (\Pi_{\text {CNO, SNO }}(\text{SC} ) \div \Pi_{\text{SNO}}(\text{S})\right)) ΠCNO, CNAME (C⋈(ΠCNO, SNO (SC)÷ΠSNO(S)))
或
Π CNO, SNO ( SC ) ÷ Π SNO ( S ) ⋈ Π CNO, CNAME ( C ) \Pi_{\text {CNO, SNO }}(\text{SC} ) \div \Pi_{\text{SNO}}(\text{S}) \bowtie\Pi_{\text {CNO, CNAME }}\left(\text{C}\right) ΠCNO, SNO (SC)÷ΠSNO(S)⋈ΠCNO, CNAME (C)
说明:涉及到全部值时,应用除法,“除数”是全部量。
(7)
Π SNO, CNO ( SC ) ÷ Π CNO ( σ TNAME=’LIU’ ( C ) ) \Pi_{\text {SNO, CNO }}(\text{SC} ) \div \Pi_{\text{CNO}} (\sigma_\text{TNAME='LIU'}(\text{C})) ΠSNO, CNO (SC)÷ΠCNO(σTNAME=’LIU’(C))19.答:
(1) Π SNO ( σ JNO = ′ J1 ′ ( SPJ ) ) \Pi_{\text {SNO}}\left(\sigma_{\text{JNO}={ }^{\prime} \text {J1}^{\prime}} (\text{SPJ})\right) ΠSNO(σJNO=′J1′(SPJ))
(2) Π SNO ( σ JNO = ′ J1 ′ ∧ PNO=’P1’ ( SPJ ) ) \Pi_{\text {SNO}}(\sigma_{\text{JNO}={ }^{\prime} \text {J1}^{\prime}}\wedge _{\text{PNO='P1'}} (\text{SPJ})) ΠSNO(σJNO=′J1′∧PNO=’P1’(SPJ))
(3) Π SNO ( σ JNO = ′ J1 ′ ∧ COLOR=’红’ ( P ⋈ SPJ ) ) \Pi_{\text {SNO}}(\sigma_{\text{JNO}={ }^{\prime} \text {J1}^{\prime}}\wedge _{\text{COLOR='红'}} (\text{P} \bowtie \text{SPJ})) ΠSNO(σJNO=′J1′∧COLOR=’红’(P⋈SPJ))
(4) Π JNO (J) − Π JNO ( σ CITY = ′ 天津 ′ ∧ COLOR=’红’ ( S ⋈ SPJ ⋈ P ) ) \Pi_{\text {JNO}} \text {(J)} - \Pi_\text {JNO} \left(\sigma_{\text{CITY}={ }^{\prime} \text {天津}^{\prime}}\wedge _{\text{COLOR='红'}} (\text {S} \bowtie \text{SPJ}\bowtie \text{P})\right) ΠJNO(J)−ΠJNO(σCITY=′天津′∧COLOR=’红’(S⋈SPJ⋈P))
(5) Π JNO, PNO ( SPJ ) ÷ Π PNO ( σ SNO=’S1’ ( SPJ ) ) \Pi_{\text {JNO, PNO }}(\text{SPJ} ) \div \Pi_{\text{PNO}} (\sigma_\text{SNO='S1'}(\text{SPJ})) ΠJNO, PNO (SPJ)÷ΠPNO(σSNO=’S1’(SPJ))
OK,以上就是本期知识点“关系操作、关系完整性、关系代数”的知识啦~~ ,感谢友友们的阅读。后续还会继续更新,欢迎持续关注哟📌~
💫如果有错误❌,欢迎批评指正呀👀~让我们一起相互进步🚀
🎉如果觉得收获满满,可以点点赞👍支持一下哟~❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页 - 如何保证一个数据(实体)是可识别的?
-
相关阅读:
Linux系统设置防火墙
Java--多线程
UserAgentUtils 用于获取 Browser和Device信息
Docker Compose学习笔记
RabbitMQ系列【7】消息可靠性之发布确认、退回机制
Unity 关节:铰链、弹簧、固定、物理材质:摩檫力、 特效:拖尾、
Linux-进程间通信
Vue CLI 3 - 创建我们的项目
高并发环境下生成序列编码重复问题分析
WSL2最佳实践,淘汰难用的Xshell和Finalshell
- 原文地址:https://blog.csdn.net/HinsCoder/article/details/126983617