VINS系统框架--原理剖析

一. VINS系统的残差项

1.1 先验残差项

---

1.2. IMU测量残差

仅仅是把预积分量当作构建残差的一把梯子而已。

IMU预积分类——IntegrationBase_yuntian_li的博客-CSDN博客

残差里面的待优化变量：i时刻的

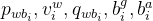
                                        j时刻的

由于构建残差项时，通用形式是，因此，构建这部分残差分为两个任务：

（1）构建IMU测量残差

（2）构建对应的协方差矩阵，用于残差项的比例分配，一个变量越准确，其方差值越小，那么其逆越大，就越相信这个变量所产生的残差。

1.2.1 构建残差

（1.2.1.1） 

蓝色项是测量值，另一部分黑色项是估计值

注意：这里直接给出各预积分量对的雅可比求法

 这里解释一下递推得到，注意，有
 

根据式（1.2.2.20），我们可以知道我们会依次计算

而

很显然有：（下标或者有点不一样，但是大致是这个道理）

其他的依次类推。

---

接下来对（1.2.1.1）求雅可比，注意只需要对估计值部分求雅可比，测量值部分相当于一个具体的数，也只有估计值部分含有我们要求导的状态变量。

---

接下来只需要对除开的状态变量求雅可比就行。

（1）速度项残差的雅可比：