CS231n课程笔记：Leture3 Loss Functions and Optimization

目录

Loss Function

multi-class SVM loss.

SHOW THE CODE FOR MULTICLASS SVM LOSS\

Regularization!

softmax

 Optimization

Gradient Descent

 iMAGE FEATURES: 

compared with CNN

---

Loss Function

Loss Function tells how good our current classifier is

Given a dataset of examples 

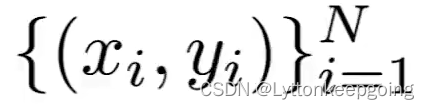
Where xi is image and yi is label

Loss over the dataset is a sum of loss over examples:

 A first example of a concrete loss function is

multi-class SVM loss.

 (is a generalization of that to handle multiple classes)

LOSS FUNCTION IN DETAILE

 

 If the true class score is much larger than the others, then formulation we often compactify into max of zero, and sj-syi+1

And this is often referred to as some type of a hinge loss.

 

Syi is the score of the true class for some training 

and Y axis is the loss.

and as the score for the true category increases ,then the loss will go down linearly until we get to above this safety margin and after which the loss will be zero.

Look the example,    

and 2.9 is a quantitative measure of how much our classifier screwed up on this one training example.

and the next car image , we can find that if the highest score is the true class. Our loss will be zero. 

So the svm loss ,remember the only thing it cares about is getting the correct score to be greater than one the incorrect scores, but in this case the car scores is already quite bit larger than the others . So if the scores for this class changed for this example changed just a little bit, this margin of one will still be retained and the loss will not change !

When we start training from scratch, usually you kind of initialize W with some small random values, as a result your scores tend to be sort of small uniform random values at the beginning of training.

SHOW THE CODE FOR MULTICLASS SVM LOSS\

def L_i_vectorized(x, y, W):
    scores = W.dot(x)
    margins = np.maximum(0, scores - scores[y] + 1)
    margins[y] = 0
    loss_i = np.sum(margins)
    return loss_i

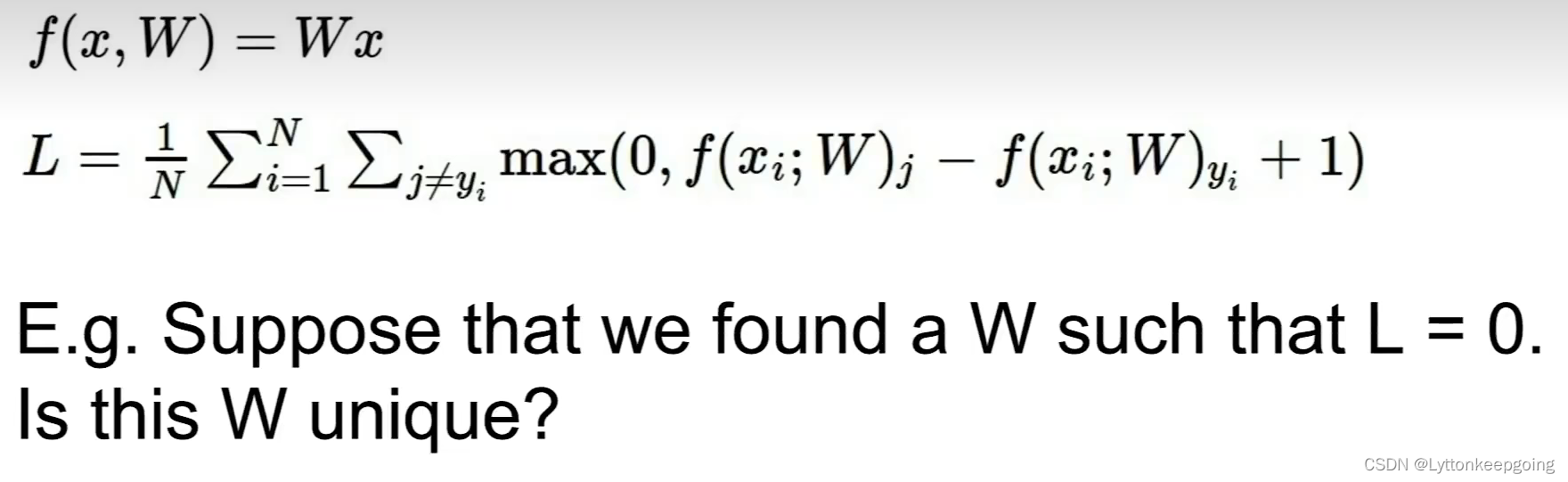
Regularization!

 except fit the training data, we'll also typically add another term to the loss function called regularization term which encourages the model to somehow pick a simpler W 

 

L1 ：sum of abs L2：Euclidean Distance

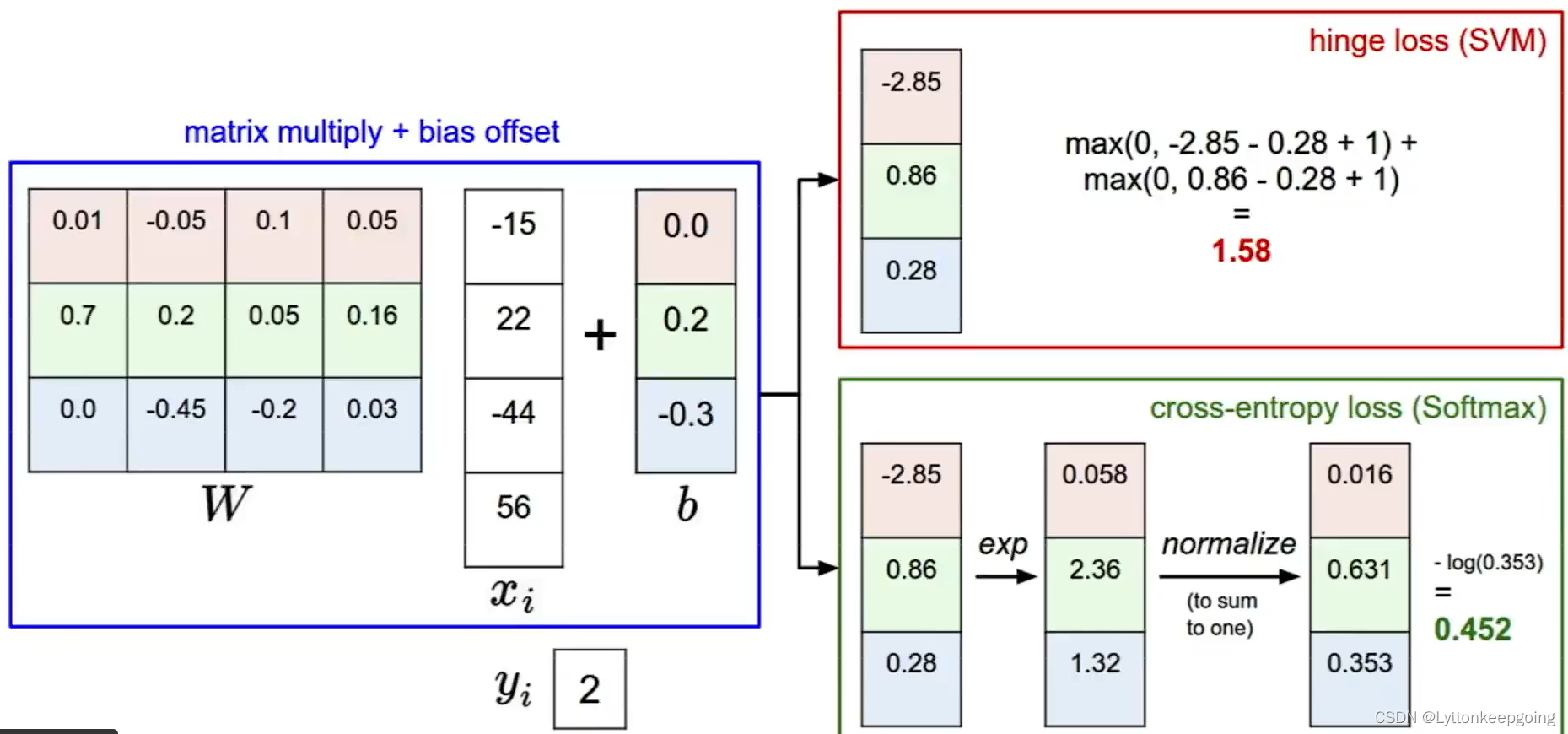
softmax

 example：

 Differences between hinge loss and cross-entropy loss

 Optimization

 What is slope？

 so if we've got some one-dimensional function f that takes in a scaler x, and then outputs the height of some curve, then we can compute the slope or derivative(导数) at any point by imagining.

The gradient is a vector of partial derivatives

example!!! how to compute the gradient dW!!! it's really really important!

 But this is actually a terrible idea, because it's super slow

rather than iterating over all the dimensions of W

We'll figure out ahead of time, what's the analytic expression for the gradient

Gradient Descent

while True:
    weights_grad = evaluate_gradient(loss_fun, data, weights)
    weights += -step_size * weights_grad # perform parameter update

step size also sometimes called a learning rate

 Instead at every iteration we sample some small set of training examples, called a minibatch

Usually this is a  power of two by convention(幂), like 16, 32,64,128

At every iteration, we use the minibatch to estimate of all sum 

Stochastic Gradient Descent (SGD)CODES:  

while True:
    data_batch = sample_training_data(data, 256) # sample 256 examples
    weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
    weigths += - step_size * weights_grad

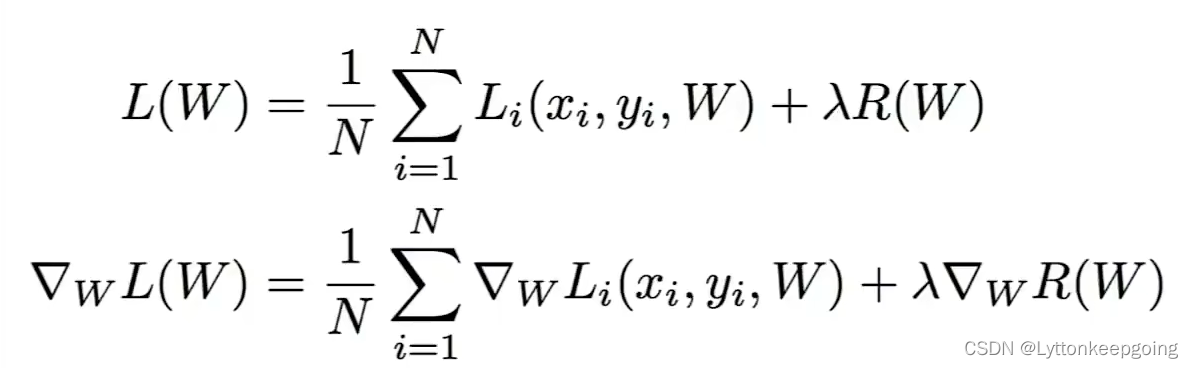
 iMAGE FEATURES: 

Motivation!

after we do the feature transform  then this complex dataset actually might become linearly separable and actually could be classified correctly.

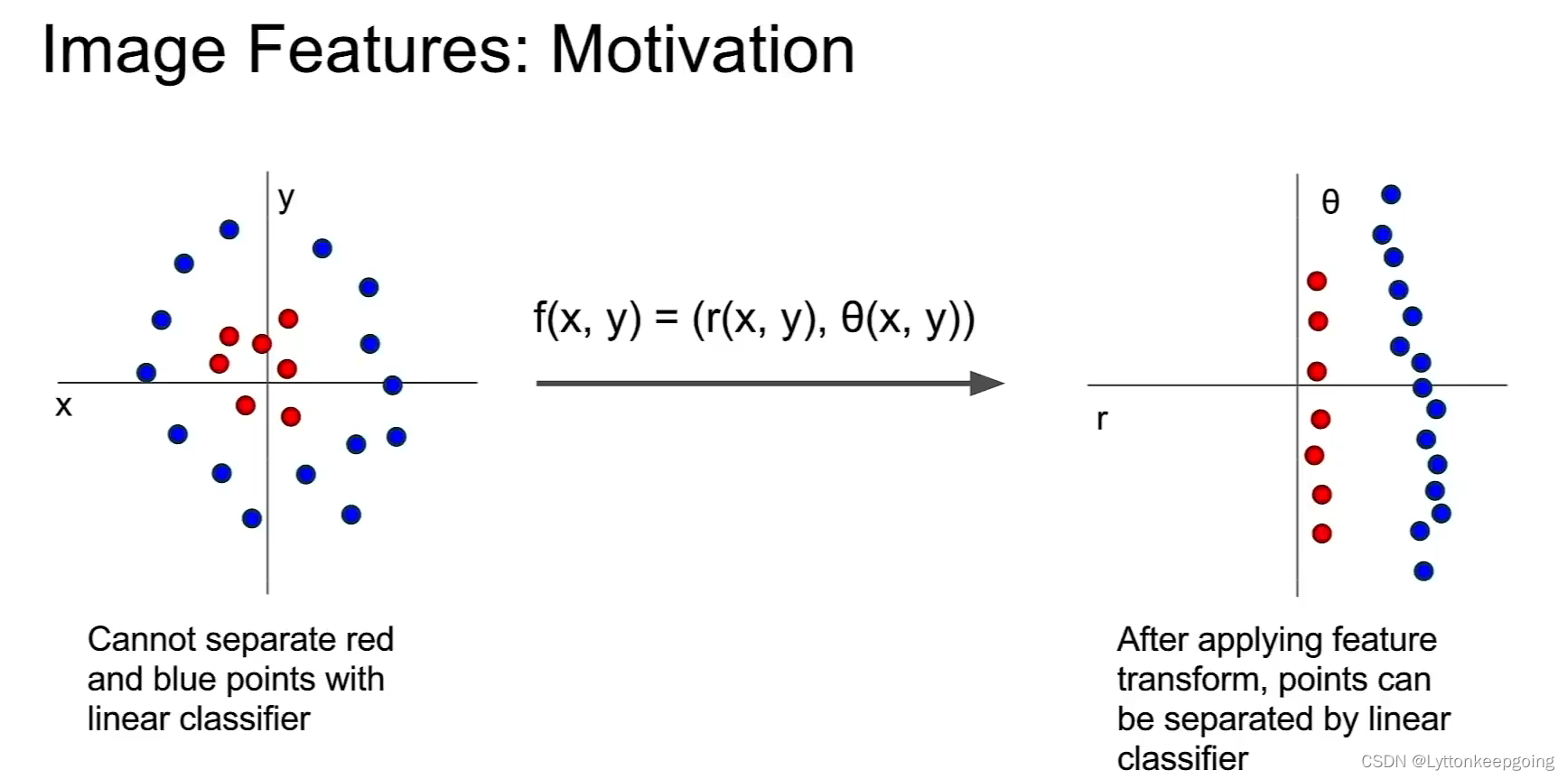
So for images, maybe converting your pixels to polar coordinates, doesn't make sense 

but you actually can try to write down feature representations of images that might make sense!

Example!

you'll take maybe each pixel, you'll take this hue color spectrum and divide it into buckets and then for every pixel, you'll map it into one of those color buckets and then count up how many pixels fall into each of these different buckets

so this tells you globally what colors are in the image!

example

compute the gradient for each pixel 

More details about HOG

(20条消息) 图像特征之（一）: 方向梯度直方图 Histogram of oriented gradient (HOG)_RaymondLove~的博客-CSDN博客another one

The feature extractor would be a fixed block that would not be updated during training

And during training , you would only update the linear classifier

compared with CNN

The only difference is that rather than writing down the features ahead of time, we're gonna learn the features directly from the data

So we'll take our raw pixels and feed them into this CNN, which will end up computing through many different layers, some type of feature representation driven by the data, and we'll train this entire weigths for this network rather than just the weights of linear classifier!