LeetCode 310 周赛

2404. 出现最频繁的偶数元素

题目描述

给你一个整数数组 nums ，返回出现最频繁的偶数元素。

如果存在多个满足条件的元素，只需要返回 最小 的一个。如果不存在这样的元素，返回 -1 。

• 1 <= nums.length <= 2000
• 0 <= nums[i] <= 10^5

示例

输入：nums = [0,1,2,2,4,4,1]
输出：2
解释：
数组中的偶数元素为 0、2 和 4 ，在这些元素中，2 和 4 出现次数最多。
返回最小的那个，即返回 2 。

思路

遍历数组，更新答案即可。

class Solution {
    public int mostFrequentEven(int[] nums) {
        Map<Integer, Integer> cnt = new HashMap<>();
        int ans = -1, maxCnt = 0;
        for (int i : nums) {
            if (i % 2 != 0) continue; // 奇数跳过
            cnt.put(i, cnt.getOrDefault(i, 0) + 1);
            if (cnt.get(i) > maxCnt) {
                maxCnt = cnt.get(i);
                ans = i;
            } else if (cnt.get(i) == maxCnt && i < ans) {
                ans = i;
            }
        }
        return ans;
    }
}

2405. 子字符串的最优划分

题目描述

给你一个字符串 s ，请你将该字符串划分成一个或多个 子字符串 ，并满足每个子字符串中的字符都是 唯一 的。也就是说，在单个子字符串中，字母的出现次数都不超过 一次 。

满足题目要求的情况下，返回 最少 需要划分多少个子字符串*。*

注意，划分后，原字符串中的每个字符都应该恰好属于一个子字符串。

示例

输入：s = "abacaba"
输出：4
解释：
两种可行的划分方法分别是 ("a","ba","cab","a") 和 ("ab","a","ca","ba") 。
可以证明最少需要划分 4 个子字符串。

思路

比较简单的贪心。这题的意思相当于要在原字符串上切上若干刀，切断之后，每一段独立的子串中的字符不会出现重复。问最少需要切多少刀。

可以这样考虑，反正一共要切若干刀。我们不妨从左到右，依次确认每一刀的位置。

一个很直观的想法是，要想使得切的刀的数量最少，那么每次应该在尽可能远的位置进行切割。即，每次切割的时候，要走的尽可能远，直到遇到了重复字符，才进行切割。我们采用这样的贪心策略来进行操作，就能保证最后划分出的子字符串的个数最少。

贪心的题目，重点在于对贪心策略正确性的证明。

下面我尝试简单的证明一下。使用反证法。

若起点是i，往右走，能走到的最远的位置是j。这表明了s[j + 1]这个字符，与区间[i, j]内的某个字符重复。而区间[i, j]内的每个字符都只出现一次。

假设我们此时切割的位置不选j，而选j之前的某个位置k，那么此时能够使得总的切割次数更小吗？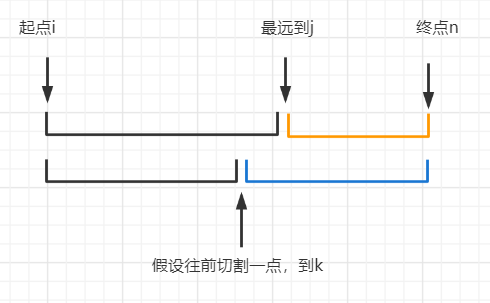

我们假设上图中橙色部分的区间的最小切割次数为t1；而蓝色部分的区间，假设其最小切割次数t2。

则一定有t2 >= t1。为什么呢？

对蓝色部分，首先考虑其和橙色部分重叠的区间，先把这部分区间切割了，则最少需要切割t1次。我们假设取t1 = 2，设切割后的第一段区间为s1，如下图。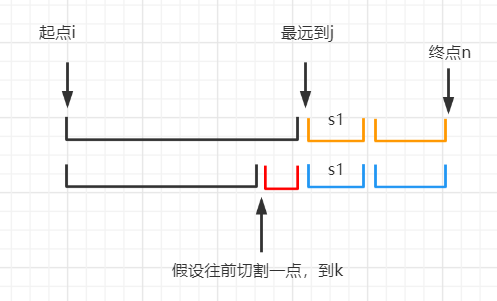

然后我们把前面的一段区间（红色部分），纳入考虑范围。（将红色的这段区间，和s1进行合并）。

由于加上了一段区间，那么字符肯定是变多了。最好的情况是：新增的这段红色区间内的字符，不会和s1中的字符发生重复（即合并后的新区间中，每个字符都只出现一次）。那么我们可以直接把这一段区间，与s1合并产生一个新的区间，而不用额外增加切割次数，这样能维持t2 = t1。

那么坏一点的情况是，红色区间中的字符本身有重复，或与s1中的字符有重复，那么对于合并后的区间，我们需要额外增加切割次数，那么此时一定有t2 > t1。

所以，对于[i, n]的切割，我们取到最远的位置j作为切割点，一共的切割次数是1 + t1。

而对于任何< j 的切割点，其总的切割次数是1 + t2。

而由于t2 >= t1恒成立，那么我们取最远的位置j作为切割点，一定能使得对于[i, n]的切割，切割次数最小。

所以我们的贪心策略是正确的。只需要从左到右遍历，每次取尽可能远的位置作为切割点即可。

class Solution {
    public int partitionString(String s) {
        // 用一个Set来记录出现的字符, 由于每个字符只能出现一次, 所以用Set就能满足需求
        Set<Integer> set = new HashSet<>();
        int ans = 0;
        for (int i = 0; i < s.length(); i++) {
            int u = s.charAt(i) - 'a';
            if (set.contains(u)) {
                ans++; // 出现重复, 进行切割
                set.clear(); // 清空计数
            }
            set.add(u);
        }
        return ans + 1;
    }
}

2406. 将区间分为最少组数

题目描述

给你一个二维整数数组 intervals ，其中 intervals[i] = [lefti, righti] 表示 闭 区间 [lefti, righti] 。

你需要将 intervals 划分为一个或者多个区间 组 ，每个区间 只 属于一个组，且同一个组中任意两个区间 不相交 。

请你返回 最少 需要划分成多少个组。

如果两个区间覆盖的范围有重叠（即至少有一个公共数字），那么我们称这两个区间是 相交 的。比方说区间 [1, 5] 和 [5, 8] 相交。

示例

输入：intervals = [[5,10],[6,8],[1,5],[2,3],[1,10]]
输出：3
解释：我们可以将区间划分为如下的区间组：
- 第 1 组：[1, 5] ，[6, 8] 。
- 第 2 组：[2, 3] ，[5, 10] 。
- 第 3 组：[1, 10] 。
可以证明无法将区间划分为少于 3 个组。

思路

这道题是一个区间的合并问题。要将数个区间进行分组，同一组内的区间不能相交。问最少划分多少个组。

这种什么最多最少，那我感觉我又要开始贪了！

要想划分的组数越少，那么很直观的，每一组中包含的区间数量应该尽可能的多。

那么如何能让一个组包含的区间尽可能多呢？

我们对每一个组，维护一下这个组中最右侧区间的右端点，称其为这个组的right。要想这个组能容纳尽可能多的区间，那么要保证该组的right增长的尽可能的慢。

我们首先对所有区间，按照左端点从小到大排序，然后用一个小根堆，来维护当前的所有组，对于所有组，维护其right属性即可。

然后遍历所有区间；判断，若当前小根堆堆顶的第一个组（right值最小的 组，都和当前这个区间相交），则需要新建一个组来存放当前区间；或者当前小根堆为空，表明当前不存在任何组，则需要新建一个组。

若当前小根堆的第一个组能够容纳当前区间，则插入进去，并更新这个组的right属性。

至于这种做法为什么是正确的，我也不清楚。哈哈，反正贪对了。具体证明等后续看了y总的视频讲解再补充了。

class Solution {
	public int minGroups(int[][] intervals) {
		// 按照区间左端点排序
		int n = intervals.length;
		quickSort(intervals, 0, n - 1); // 这里可以直接用Arrays.sort的API
		PriorityQueue<Integer> q = new PriorityQueue<>();
		for (int[] i : intervals) {
			int l = i[0], r = i[1];
			if (q.isEmpty() || q.peek() >= l) q.offer(r);
			else {
				q.remove(q.peek());
				q.offer(r);
			}
		}
		return q.size();
	}

	private void quickSort(int[][] arr, int l, int r) {
		if (l >= r) return ;
		int x = arr[l + r >> 1][0], i = l - 1, j = r + 1;
		while (i < j) {
			do i++; while (arr[i][0] < x);
			do j--; while (arr[j][0] > x);
			if (i < j) {
				int[] t = arr[i];
				arr[i] = arr[j];
				arr[j] = t;
			}
		}
		quickSort(arr, l, j);
		quickSort(arr, j + 1, r);
	}
}

2407. 最长递增子序列 II

题目描述

给你一个整数数组 nums 和一个整数 k 。

找到 nums 中满足以下要求的最长子序列：

• 子序列 严格递增
• 子序列中相邻元素的差值 不超过 k 。

请你返回满足上述要求的 最长子序列 的长度。

子序列 是从一个数组中删除部分元素后，剩余元素不改变顺序得到的数组。

• 1 <= nums.length <= 10^5
• 1 <= nums[i], k <= 10^5

示例

输入：nums = [4,2,1,4,3,4,5,8,15], k = 3
输出：5
解释：
满足要求的最长子序列是 [1,3,4,5,8] 。
子序列长度为 5 ，所以我们返回 5 。
注意子序列 [1,3,4,5,8,15] 不满足要求，因为 15 - 8 = 7 大于 3 。

思路

这题是经典的最长递增子序列（LIS）的变种。多加了一个约束：子序列中相邻元素相差不能超过k。周赛当天我直接套用LIS的思路，采用贪心加二分。

class Solution {
	public int lengthOfLIS(int[] nums, int k) {
		// f[i] 表示长度为i的子序列, 末尾的最小值
		int n = nums.length;
		int[] f = new int[n + 1];
		int len = 0;
		for (int e : nums) {
			int l = 0, r = len;
			while (l < r) {
				int mid = l + r + 1 >> 1;
				if (f[mid] < e) l = mid;
				else r = mid - 1;
			}
			// 插入
			if (len == 0 || e - f[l] <= k) {
				f[l + 1] = e;
				len = Math.max(len, l + 1);
			}
		}
		return len;
	}
}

提交发现只能通过78个用例

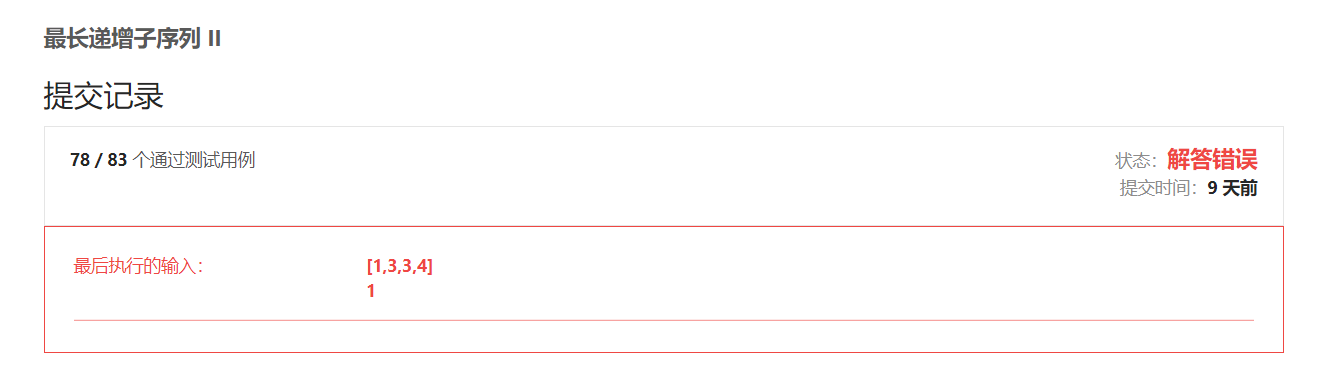
我们来看一下这组数据：[1,3,3,4]

很明显，满足相邻元素相差不超过k = 1，的最长递增子序列，是[3,4]，长度为2。

而我们的贪心策略，是用f[i]表示长度为i的子序列，结尾最小的值。对于这组数据，f[1] = 1，而1结尾，则无法与后面的3和4进行合并。而我们的贪心策略f[i]维护的是末尾最小值，就无法使得f[1]更新为3。只有f[1]能够更新为3后，才能与后面的4进行结合，得到长度为2的递增子序列。

那么换一种思路，那我对所有位置作为起始位置，都求一遍LIS，可以吗？

class Solution {
	public int lengthOfLIS(int[] nums, int k) {
        // 以位置i作为起点, 求解LIS
		Map<Integer, List<Integer>> map = new HashMap<>();
		int ans = 0;
		for (int i = 0; i < nums.length; i++) {
            // 第一个位置作为占位, 以处理边界问题
			if (!map.containsKey(i)) map.put(i, new LinkedList<>(Arrays.asList(0)));
			for (int key : map.keySet()) {
				List<Integer> ff = map.get(key);
				int l = 0, r = ff.size() - 1;
				while (l < r) {
					int mid = l + r + 1 >> 1;
					if (ff.get(mid) < nums[i]) l = mid;
					else r = mid - 1;
				}
				// 插入
				if (ff.size() - 1 == 0 || l == 0 || (nums[i] - ff.get(l) <= k && nums[i] > ff.get(l))) {
					if (l + 1 < ff.size()) ff.set(l + 1, nums[i]);
					else ff.add(nums[i]);
					ans = Math.max(ans, ff.size() - 1);
				}
			}
		}
		return ans;
	}
}

这样能过掉上面的那组数据[1,3,3,4] 1。但提交后发现还是WA。

WA的数据是：[10,3,20,2,16,12] 4。我的代码的输出是1，而正确答案应该是2（[10, 12]）。

分析发现，当对第一个位置求LIS时，其会被后面的3给更新掉，使得以i = 0这个位置求解LIS时的f[1]变为了3，则无法和后面的12进行组合。可以看到，二分是行不通的。因为无法按照维护末尾最小值这种贪心思路来求得正确答案。

于是再来盯着最朴素的 $O(n^2)$ 的动归思路。

对于最长上升子序列问题，我们用动态规划的思路是：

设f[i]表示，结尾数字为nums[i]的所有子序列中，最长子序列的长度。

对于结尾数字为nums[i]的子序列，我们如何进行状态转移呢？考虑倒数第二个数字，倒数第二个数字可以取nums[i - 1]，nums[i - 2]，nums[i - 3]，…

那么。状态转移方程为：f[i] = max{ f[j] } + 1，其中j的取值范围是[0, i - 1]，注意必须满足nums[i] > nums[j]的位置，才能参与到状态转移当中。

这道题目，再最长上升子序列的基础上，添加另一个额外约束：相邻元素相差不超过k，那么状态转移方程中的条件，除了需要满足nums[i] > nums[j]，还需要满足nums[i] - nums[j] < k。

可以发现只需要增加一个条件即可。但是这道题的数据范围是10^5，动态规划的复杂度是$O(n^2)$，会超时。所以我们需要对状态转移的过程进行优化。主要是求解max {f[j]} 这一步，朴素的动归中，使用的是遍历，这种求区间内的最值，可以使用线段树这种数据结构，在$O(logn)$的复杂度完成求解，即可把整个算法的复杂度降低为 $O(nlogn)$。但这个数据结构我还需要补课！

看了一下题解，大概都是说线段树的（其中有个讲分治+单调队列的，横竖都看不懂），无奈这个数据结构我还没学过。先去补课！

------把线段树的基本原理补了一遍。这里大概说一下，线段树的具体笔记等后续学了算法提高课后再做补充。

线段树的基本原理描述如下：

线段树首先是一颗二叉树，并且通常是一颗近似完美的二叉树（除了最后一层节点，其余部分是一颗满二叉树）。线段树通常是用来维护一段区间内的某种信息的。

假设我们用一颗线段树来表示区间[1,10]，表示的信息是区间的和。那么这颗线段树的根节点表示整个区间[1,10]，根节点的值为区间[1,10]的和，根节点有2个子节点，2个子节点会把根节点所代表的区间平均分成两份，左子节点表示区间[1,5]，右子节点表示区间[6,10]，然后每个节点所代表的区间，再继续往下分，直到不可再分为止（树上的节点表示的区间是单点的区间）。如下图所示。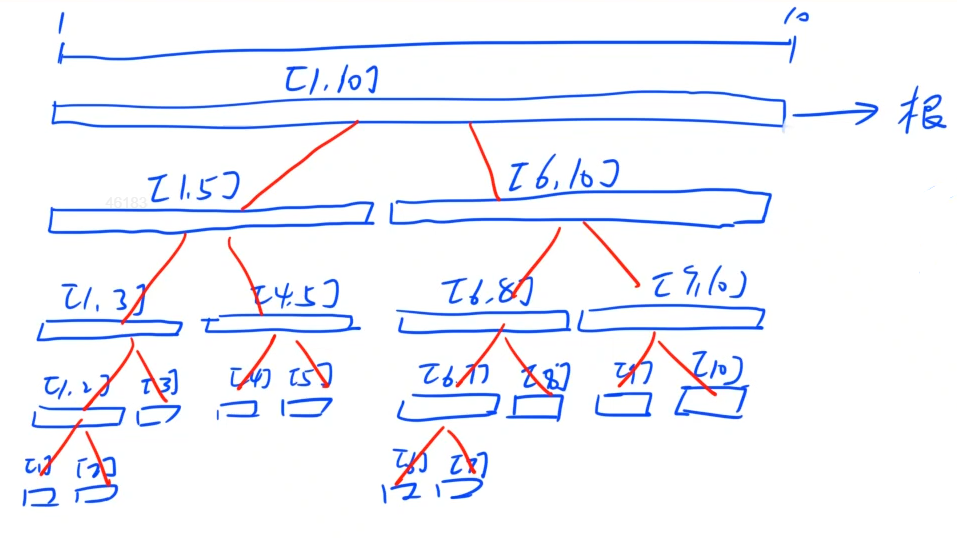

其主要优点是可以对区间内的信息进行动态修改。使得查询某段区间的时间复杂度为$O(logn)$，修改某段区间时间复杂度也为$O(logn)$。对于上面的，维护区间和，其实可以使用前缀和，能够在$O(1)$的复杂度内求得某段区间的和，但是前缀和的局限性在于，无法对区间内的值做修改，一旦做了修改，需要用$O(n)$的复杂度来更新整个前缀和数组。

所以线段树的适用场景，通常是用来求解区间问题，并且区间内的数据可以做动态修改。比如给定一个数组nums，其长度为n。再给出m次操作，每次操作有两种选择：

• 查询下标在[L, R]范围内的最大值
• 修改某个下标i的元素的值

这类问题，便是线段树的经典应用。

由于这道题，我们可以用动态规划的思路来做，但是动归的过程中需要求解一个max {f[j]}，这个过程便可以用线段树来优化，将时间复杂度从 $O(n)$ 降低到 $O(logn)$，使得整体复杂度降为$O(nlogn)$。

我们先将整个动态规划的思路用代码实现一下。注意对于状态f的定义，第二个维度，我们定义时是结尾的数字，而不是下标，这与前面的描述不一致，主要是为了方便使用线段树。

class Solution {
    public int lengthOfLIS(int[] nums, int k) {
        // 用f[i][j] 表示从[0,i]区间中取, 最后一个元素是j的满足条件的子序列中, 长度最长的子序列的长度
        // 当nums[i] != j 时, f[i][j] = f[i - 1][j]
        // 当nums[i] == j 时, f[i][j] = 1 + max {f[i - 1][j']}, 其中 j - j' <= k, 即 j > j' >= j - k
        // 由于f[i][j] 都是从 f[i - 1][j] 转移过来, 我们可以用滚动数组思想, 优化为1维

        int n = nums.length;
        int maxJ = 0;

        // 求一下最大的j
        for (int i = 0; i < n; i++) maxJ = Math.max(maxJ, nums[i]);
        
        // 定义f
        int[] f = new int[maxJ + 1];
        
        // 状态转移
        for (int i = 0; i < n; i++) {
            int j = nums[i];
            // 只需要更新f[i][j]
            int max = 0;
            for (int jj = Math.max(0, j - k); jj < j; jj++) {
                max = Math.max(max, f[jj]);
            }
            f[j] = max + 1;
        }

        int ans = 0;
        for (int i = 0; i <= maxJ; i++) ans = Math.max(ans, f[i]);
        return ans;
    }
}

这份代码提交会报TLE，因为其复杂度达到了 $O(n^2)$，对于求解max {f[i-1][j']} 这一步，我们用线段树来优化。

max {f[i - 1][j']}实际就是求解区间[j - k, j - 1]的最大值，故可以用线段树来优化。

线段树的存储通常用一维数组（类似于用一维数组来存储堆），需要开的节点个数，经过计算，需要开整个区间点的数量的4倍。

class Solution {

	int[] f;
	public int lengthOfLIS(int[] nums, int k) {
		//用f[i][j] 表示从[0,i]区间中取, 最后一个元素是j的满足条件的子序列中, 长度最长的子序列的长度
		// 当nums[i] != j 时, f[i][j] = f[i - 1][j]
		// 当nums[i] == j 时, f[i][j] = 1 + max {f[i - 1][j']}, 其中 j - j' <= k, 即 j > j' >= j - k
		// 由于f[i][j] 都是从 f[i - 1][j] 转移过来, 我们可以用滚动数组思想, 优化为1维

		int n = nums.length;
		int maxJ = 0;
		// 求一下最大的j
		for (int i = 0; i < n; i++) maxJ = Math.max(maxJ, nums[i]);

		// 初始化线段树, 开4倍大小
		f = new int[4 * maxJ];

		// 状态转移
		for (int i = 0; i < n; i++) {
			int j = nums[i];
			// 只需要更新f[i][j]
            if (j == 1) {
                // j - 1 = 0了, 此时
                modify(1, 1, maxJ, 1, 1);
                continue;
            }
			int l = Math.max(1, j - k), r = j - 1;
            // 先求出f[j], 注意这里要暂存
			int t = query(1, 1, maxJ, l, r) + 1;
			// 更新一下线段树
			modify(1, 1, maxJ, j, t);
		}
		// 根节点表示整个区间的最大值, 即max {f[0], f[1], ...., f[maxJ] }
		return f[1];
	}

	// idx 是线段树上的当前节点编号, 根节点编号为1
	// [tl, tr] 是当前节点代表的区间
	// [L, R] 是待查询的区间
	private int query(int idx, int tl, int tr, int L, int R) {
		// 包含这段区间, 直接返回
		if (L <= tl && R >= tr) return f[idx];
		int mid = tl + tr >> 1;
		int ret = 0;
		// 需要查询左儿子
		if (L <= mid) ret = query(idx << 1, tl, mid, L, R);
		// 需要查询右儿子
		if (R > mid) ret = Math.max(ret, query(idx << 1 | 1, mid + 1, tr, L, R));
		return ret;
	}

	// x 是待修改的单点
	// newVal 是新的值
	private void modify(int idx, int tl, int tr, int x, int newVal) {
		// 到达叶子节点
		if (tl == tr) {
			f[idx] = newVal;
			return ;
		}
		int mid = tl + tr >> 1;
		// 要修改的节点在左子树上
		if (x <= mid) modify(idx << 1, tl, mid, x, newVal);
			// 在右子树上
		else modify(idx << 1 | 1, mid + 1, tr, x, newVal);
		// 左右子树修改完毕后, 更新下当前节点
		f[idx] = Math.max(f[idx << 1], f[idx << 1 | 1]);
	}
}

总结

本次周赛表现不错，前3题在半个小时内就都做出来了，然后最后一题坐牢了1个小时。第4题属于没办法，没学过线段树。用线段树是比较好想的，也有其他的不使用线段树的解法，有待后续再研究了。