-
通信原理学习笔记3-4:数字通信系统性能指标(带宽、信噪比Eb/N0、可靠性与误码率、有效性与频谱利用率)
数字系统占用的带宽
为了便于理解分析数字系统带宽,给出如下模型(实际中模型并非如此)

要注意的是:
- 虽然理论上数字基带信号使用矩形脉冲分析,但实际中都是类似sinc的脉冲(由上图「脉冲成形」的升余弦滤波器提供),从而节省带宽、且在接收端抽样判决时可以减少码间串扰
使用sinc的脉冲,也会导致实际看到的PSK/QAM等已调波形与理想的波形不同,因为理想波形都是以矩形脉冲为前提的(例如BPSK: y ( t ) = x ( t ) cos 2 π f t y(t)=x(t)\cos 2\pi ft y(t)=x(t)cos2πft,其中 x ( t ) x(t) x(t)就是矩形脉冲),但我们不需要关注时域已调波形与理论的差异,只要接收端能还原基带脉冲信号(相干解调),并正确抽样判决即可
我们在信道上传输的是脉冲成形后的码元(一个脉冲波形对应一个码元),因此带宽应该从码元级别来看(而非信息比特),也就是说:
- 基带脉冲成形后,基带信号带宽取决于基带成形脉冲信号的能量谱,并和 R s R_s Rs(或着说码元周期 T s = 1 / R s T_s=1/R_s Ts=1/Rs)挂钩:
重要结论
- 矩形脉冲:绝对带宽无限,第一零点带宽
B
=
R
s
=
1
/
T
s
B=R_s=1/T_s
B=Rs=1/Ts
对于归零RZ矩形脉冲,第一零点带宽翻倍: B = 2 R s B=2R_s B=2Rs - sinc脉冲:基带带宽 B = R s / 2 B=R_s/2 B=Rs/2,这是最理想情况,即满足Nyquist准则的无码间串扰的最小带宽
- 升余弦滚降滤波器形成的形似sinc的脉冲:基带带宽 B = ( 1 + α ) R s / 2 B=(1+\alpha)R_s/2 B=(1+α)Rs/2,实际采用的脉冲,同样满足Nyquist准则,但占用的带宽比理想情况稍大
- 频带信号带宽 取决于基带脉冲信号 以及 上变频的方式(上图的“模拟调制”),因此同样和 R s R_s Rs挂钩
例如,考虑最理想的sinc脉冲,则基带带宽 B = R s / 2 B=R_s/2 B=Rs/2;
如果是双边带调制的上变频,则频带带宽 W = 2 B = R s W=2B=R_s W=2B=Rs信噪比SNR和 E b / N 0 E_b/N_0 Eb/N0
模拟通信系统中,信噪比一般用 S / N S/N S/N衡量;数字通信系统中,信噪比一般用 E b / N 0 E_b/N_0 Eb/N0衡量;
实际上,两种指标的本质是相同的,推导如下:
E b E_b Eb为平均每比特能量, N 0 / 2 N_0/2 N0/2为噪声双边功率谱密度, B B B为基带信道带宽,噪声总功率为 N 0 2 × 2 B = N 0 B \frac{N_0}{2}\times2B=N_0B 2N0×2B=N0B(也可以用噪声单边功率谱密度N0乘以带宽B得到)
信噪比就是信号功率和噪声功率的比: S N = E b N 0 ⋅ R b B \frac{S}{N}=\frac{E_b}{N_0}\cdot\frac{R_b}{B} NS=N0Eb⋅BRb
其中分子的含义是:信号能量*传输速率=信号功率写为对数形式,就是 S N R ( d B ) = 10 l o g 10 ( E b N 0 ) + 10 l o g 10 ( R b B ) = E b N 0 ( d B ) + R b B ( d B ) SNR(dB)=10log_{10}(\frac{E_b}{N_0})+10log_{10}(\frac{R_b}{B})=\frac{E_b}{N_0}(dB)+\frac{R_b}{B}(dB) SNR(dB)=10log10(N0Eb)+10log10(BRb)=N0Eb(dB)+BRb(dB)
前面说过,基带信道带宽 B B B取决于基带脉冲信号、上变频的方式,因而与 R s R_s Rs挂钩,例如采用理想sinc脉冲成形,双边带调制,则 B = R s / 2 B=R_s/2 B=Rs/2;
从而在数字调制方式和脉冲成形滤波器确定后, R b B \frac{R_b}{B} BRb是一个常数,因此对数下的 S / N S/N S/N和 E b / N 0 E_b/N_0 Eb/N0没有只是相差一个常数,没有本质区别有效性
数字通信系统的有效性用频谱资源利用率来衡量:
η = 信 息 量 传 输 时 间 × 信 道 带 宽 = R b W ( b p s / H z ) \eta=\frac{信息量}{传输时间\times 信道带宽}=\frac{R_b}{W}(bps/Hz) η=传输时间×信道带宽信息量=WRb(bps/Hz)分母的带宽,如果带入基带带宽,就是基带频谱资源利用率;带入频带带宽,就是频带频谱资源利用率;
若采用双边带调制,基带频谱资源利用率=频带频谱资源利用率x2;
有时分子也带入 R s R_s Rs计算,则此时单位变为Baud/Hz例如,采用理想sinc脉冲成形,双边带调制,则 W = 2 B = R s W=2B=R_s W=2B=Rs,进而有 η = R b W = R b R s \eta=\frac{R_b}{W}=\frac{R_b}{R_s} η=WRb=RsRb可见,由于 R b = l o g 2 M R s R_b=log_2MR_s Rb=log2MRs,调制阶数 M M M越高,调制效率 η \eta η越高;
当然调制阶数增高,也会导致星座图中点间距变小,可靠性降低频谱资源利用率的上限
比特速率 R b R_b Rb和信噪比 E b / N 0 E_b/N_0 Eb/N0固定的情况下(基带滤波也固定),则调制编码方式决定了频谱资源利用率
虽然可以优化调制方式(增加调制阶数),增加频谱利用率,但是频谱资源利用率有上限(一个码元承载过多比特,终究会导致大量误码、无法可靠通信),这个上限由 E b / N 0 E_b/N_0 Eb/N0决定
[推导] 频谱利用率(传输速率 R b R_b Rb与带宽 B B B的比值)和信噪比 E b / N 0 E_b/N_0 Eb/N0的关系
信息传输速率最大,应将 R b = C R_b=C Rb=C代入信噪比 S N = E b N 0 ⋅ R b B \frac{S}{N}=\frac{E_b}{N_0}\cdot\frac{R_b}{B} NS=N0Eb⋅BRb
带入香农公式: C = B l o g 2 ( 1 + S / N ) = B l o g 2 ( 1 + E b N 0 ⋅ C B ) C=Blog_2(1+S/N)=Blog_2(1+\frac{E_b}{N_0}\cdot\frac{C}{B}) C=Blog2(1+S/N)=Blog2(1+N0Eb⋅BC),
可以得到 E b N 0 \frac{E_b}{N_0} N0Eb和 C B \frac{C}{B} BC满足关系: E b N 0 = 2 C / B − 1 C / B \frac{E_b}{N_0}=\frac{2^{C/B}-1}{C/B} N0Eb=C/B2C/B−1,或 E b N 0 ( d B ) = 10 l o g 10 ( 2 C / B − 1 C / B ) \frac{E_b}{N_0}(dB)=10log_{10}(\frac{2^{C/B}-1}{C/B}) N0Eb(dB)=10log10(C/B2C/B−1)
关系如图:
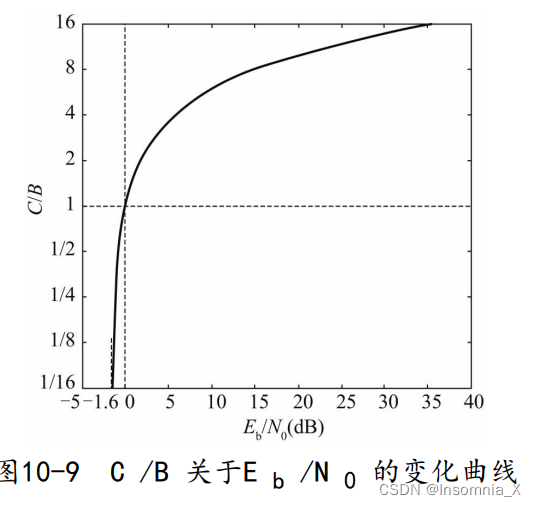
注意,这里讨论的是基带频谱资源利用率 C / B C/B C/B,若采用双边带调制,频带频谱资源利用率为它的一半- 信噪比 E b / N 0 E_b/N_0 Eb/N0决定了基带频谱资源利用率的上限 R b B = C B \frac{R_b}{B}=\frac{C}{B} BRb=BC
- 基带频谱资源利用率
C
/
B
C/B
C/B随着
E
b
/
N
0
E_b/N_0
Eb/N0增大而增大
但由于信号发射功率不可能无限大,所以频谱资源利用率也不可能无限大 - 基带频谱资源利用率
C
/
B
C/B
C/B随着
E
b
/
N
0
E_b/N_0
Eb/N0减小而减小,
E
b
/
N
0
E_b/N_0
Eb/N0趋于
−
1.6
d
B
-1.6dB
−1.6dB(香农极限)时,
C
/
B
C/B
C/B趋于
0
0
0
这表明,要实现无差错的数据传输,信噪比必须高于一定水平( E b / N 0 E_b/N_0 Eb/N0低于 − 1.6 d B -1.6dB −1.6dB不可能实现无差错的数据传输)
狭义香农极限:(通过编码实现)无差错传输,所需的最小信噪比,约为-1.6dB
广义香农极限:要达到给定的误码率,所需的最小信噪比
香农第二定理指出,只要信息传输速率小于信道容量,一定存在一种信道编码,使得信息传输错误概率任意小
香农第二定理对应的 [最大信息传输速率(信道容量C)下,无错传输所需的最小信噪比],正是对应这里的狭义香农极限可靠性
数字通信系统的有效性用误比特率BER来衡量,误比特率通常随着信噪比 E b / N 0 E_b/N_0 Eb/N0增大而降低
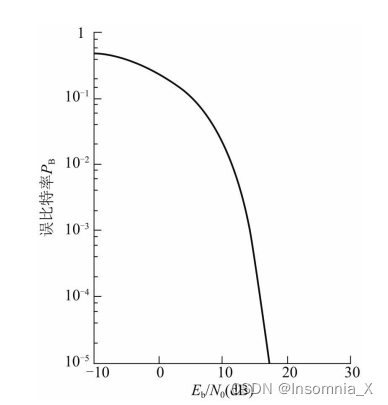
提高可靠性 / 改善误比特率,有两个思路:
①提高信噪比:信号发射功率不可能无限提高,所以信噪比总是有限的
②信道编码:增加的冗余信息来实现纠错,但显然占用了一部分传输资源,有效性降低例如(2,1,3)卷积码,输入1 bit,编码器输出2 bit,信道编码后,若要保持有用信息传输速率 R b R_b Rb不变,则信道编码后的波特率 R s R_s Rs变为原来两倍,进而占用带宽 W = R s W=R_s W=Rs也变为原来两倍,因此频谱资源利用率 η \eta η减半,有效性降低

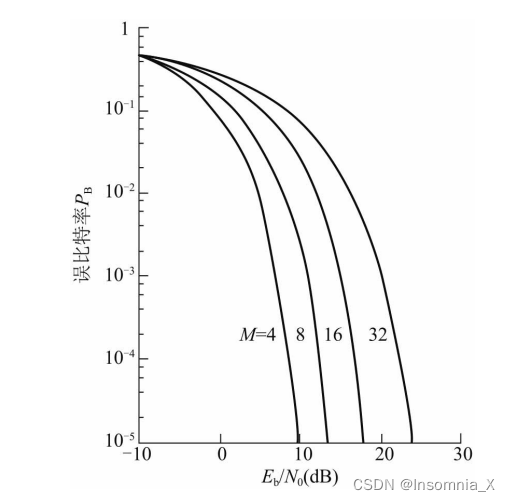
另外,之前也说过,PSK调制阶数增加,虽然有效性更好(频谱利用率升高),但可靠性变差(星座点更靠近)
可见,通信系统的可靠性和有效性总是相互制约的,实际中应该根据不同需要做权衡
-
相关阅读:
电子笔记真的好用吗?手机上适合记录学习笔记的工具
2021年亚太杯APMCM数学建模大赛C题生态保护的建设及其对环境影响的评价求解全过程文档及程序
虚拟机ubantu系统突然重启失去网络
自定义线程实现c++代码回调run方法
集成环信IM时常见问题及解决——包括消息、群组、推送
设计模式之工厂方法模式--更加符合开闭原则的工厂模式
HCIP第十八天笔记
接口自动化测试完整版(文档+视频)
吴恩达《机器学习》8-3->8-4:模型表示I、模型表示II
贪心算法 Greedy Algroithm
- 原文地址:https://blog.csdn.net/Insomnia_X/article/details/126021039