EEG时频主成分分析（TF-PCA）实用教程（附示例数据和代码）

时频主成分分析（TF-PCA）提供了一种数据缩减方法，它不依赖于关于感兴趣效应的特定时间或频率边界的先验约束，因此特别适合于存在认知发展变化的TF数据分析。本教程提供了背景知识、理论和实用指导，文章还附带了一个配套的GitHub存储库，该存储库包含示例代码、数据和如何执行TF-PCA的逐步指南：https://github.com/NDCLab/tfpca-tutorial。

1.理论和方法介绍
1.1 脑电图时频（TF）表征方法简介
TF表征（Time-frequency representation）描述了一个时变信号，如脑电图波形，在时间变化下特定频率的活动（用功率强度表示）。TF表征可以绘制成一个谱图，包含两个空间维度（x和y轴）和第三个非空间维度映射到颜色值（如图1所示）。将时域脑电图信号分解为TF表征的方法有多种方法，最常见的方法是利用Morlet小波进行连续小波变换（CWT)，但缺点是它倾向于在低频率段和高频率段产生“涂抹”，避免这种问题就要对感兴趣的频率段所在边界有很强的先验知识，然后控制CWT/Morlet方法的参数（即母小波中的周期数）以提高特定频带的时频分辨率。Cohens Class Reduced Interference Distribution(RID）方法能够在时域和频域上产生跨越所有频段的相对较高的分辨率，较少依赖频率边界的先验知识，更适合于缺乏先验知识的发展研究中。因此，本文关注于RID方法上，但TF-PCA的核心逻辑应用于任何TF变换方法，包括使用Morlet小波的CWT。

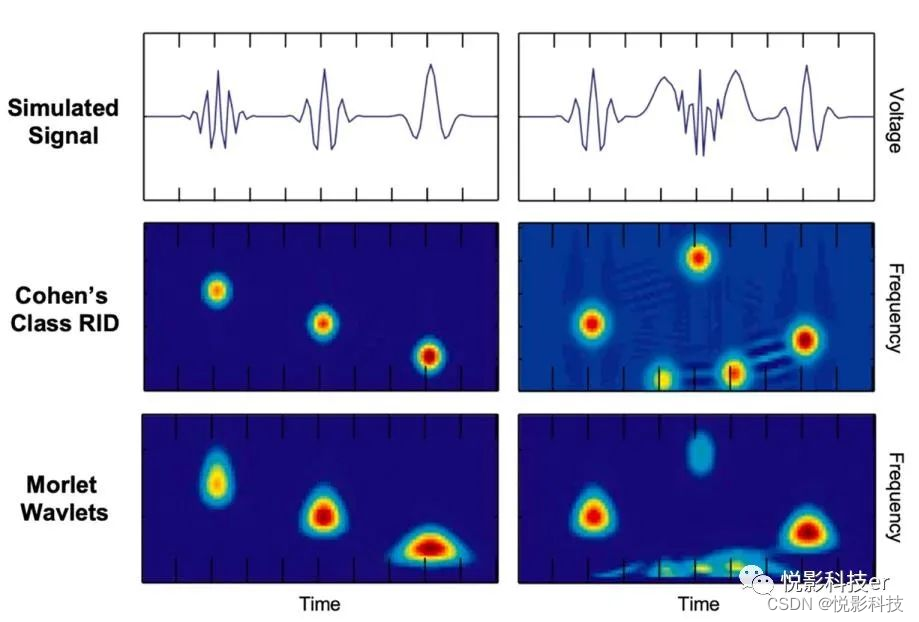
图1：使用Morlet小波与RID方法产生的时频表征

1.2 脑电图TF表征的数据缩减方法
一种分析思路是将TF表征中的所有点（和/或所有电极位置）进行统计分析，并以某种方式纠正大量的多重比较（例如，通过LIMO工具箱）。这种方法对于检测感兴趣的效应特别有用，但是在统计分析之前减少要比较的数据将更有效。最常见的方法之一是在时间和频率上定义一个矩形的“感兴趣区域”(ROI)，然后计算这个ROI内的平均值，但这个方法也是需要先验知识。所以，现在有利用数据驱动的方式来寻找ROI，比如独立成分分析（ICA)。ICA计算一组空间加权矩阵，将原始的脑电图信号分离成一组相互独立的（非高斯）因子，代表与ROI的TF表征有关的独立源神经活动。脑电ICA主要用在个体水平，在组水平分析独立ICA成分仍存在困难，但TF-PCA将TF表征减少到少量的主成分（通常在1-5成分的范围内），可以在不同的参与者或条件之间进行统计比较。而且， TF-PCA使用TF表征进行计算，并反映了所有TF点的权重，不需要在时间和频率维度上定义ROI。

1.2.1 主成分分析（PCA）的简介
主成分分析对变量间的相关性矩阵或协方差矩阵进行特征分解，返回各变量相同的特征向量（因子），每个特征向量的长度等于原始相关/协方差矩阵中的变量数。将每个特征向量投影到一个新的特征空间中，与给定特征向量相关的特征值描述这个新特征空间内的大小，给定因子的特征值就可用于识别给定特征向量（因子）所保留的信息量（方差解释）。最后，将一个因子乘以其特征值的平方根将得到一个此因子的一组载荷。总之，PCA的目的就是数据降维，所以通过方差解释度（界值可以设为60-80%间）或碎石图确定因子数目是关键。一旦确定了因子数目，通常会应用因子旋转（正交或斜向）来产生一组载荷（“权重”），其格式更容易解释且与原始数据相关联。

1.2.2 TF-PCA方法的概述
第一步（图2B）：为每个感兴趣的条件的每个通道计算TF表征（可以是时间窗平均也可以是条件平均）
第二步（图2C）：通过端到端连接每个TF表征（也可以基于选择的TF表征）中的每一行（对应于单个频率段随时间的变化），使得每个TF表征从其原生矩阵组织转换为一个向量
第三步（图2D）：将特征分解应用于每个长向量（代表一个TF表征）。选择一个适当的PCA因子解数量，并应用一个Varimax旋转，为每个提取的因子产生一个权重向量（负荷）。然后将每个因子权值的向量转换回与原始TF表征的维数对应的原生矩阵组织。
第四步（图2E）：对于每个提取的感兴趣的成分，因子权重矩阵乘以原始的TF表征（或相关的TF表征），以分离感兴趣的TF-PCA成分。
第五步（图2F）：提取的TF-PCA成分以类似于传统TF数据的方式进行统计分析

图2：TF-PCA中所涉及的步骤的概述

2. TF-PCA的分析要点
2.1 TF-PCA可以分析非平均（锁相）功率的变化
TF-PCA可以直接应用于总功率的TF表征（包括锁相和非锁相功率），以及基于相位度量TF表征（例如，在电极内或跨电极内计算的相位同步度量）等。当TF-PCA直接应用于TF表征总功率，产生的成分往往时间离散度下降，或（相比成分来自TF表征平均功率）没有“涂抹”。分析总功率（和/或相位）的TF表征是为确定数据集的一组TF-PCA成分，然后将这些成分应用于来自同一数据集的不同TF表征（例如，平均功率、总功率）。但迄今为止，最常见的方法是对平均功率的TF表征执行TF-PCA，然后将TF主成分应用于总功率和相位表示。当然，这两种方法也可以混合使用，最后生成的结果是一系列平均功率的主成分加权TF表征，以及总功率（和/或相位），然后可以绘制和统计分析。重要的是，要准确地理解由此产生的主成分加权TF表征反映了什么，以及它们何时可用和与其他导出的EEG/ERP测量值的关系。总之，这种方法适合研究人员对研究总功率的TF表征感兴趣，同时又要保持锁相活动中相对较高的时间精度的情况下。

2.2 常见的问题和实际的考虑
2.2.1 进行TF-PCA的数据量要求
进行PCA需要一定量的数据。一般统计原则，每个变量至少需要5个观测值，为确定数据量的下限，TF特征数据似乎更稀疏可以放低一点要求，但是仍然需要明确变量数和观察数分别代表什么。对于EEG数据，变量数和用于提取特征根的TF特征中的采样点数量一致，而观察数是被试数、条件以及通道数（参与者x条件x通道=总观测数），如果有trial水平，再乘以试次数，一般一个数据集就有固定的观察数，而变化的主要是受采样率影响的变量数。一般500Hz的采样率的数据只关注9Hz以下的频段，那么研究者就可以将采样率降低到32Hz（4倍以上）。也可以保持原采样率而调整时间窗。在实践中，在进行TF-PCA时，通常会使用这两种方法的组合来增加观察量与变量的比率。总之，只要所使用的数据具有较好的质量（使用单次试验数据的质量较差），并且有足够的观察数与变量数的比例（类似于传统的ERP分析中的信噪比），使用观察量和变量的组合来执行TF-PCA是有效的。

2.2.2 确定合适的因子数
如果有先验知识能确定因子成分，这就有助于检查PC加权的TF特征的可视化结果。可视化的结果也可以是特定条件下或者是对比条件下的结果，基于研究目的，可以选择单一条件下的分组因子报告，还是利用因子差值进行报告。比如，研究关注的是两种条件下theta波活动在中脑区域的差异，就适合分组提取因子数；关注的是条件下的脑活动与心理变量之间的关系，那就适合合并提取因子。总之，不管目的如何，都需要详细报告如何确定因子数的流程和步骤。

2.2.3 低频数据TF-PCA导致解饱和问题
实际上，当TF表征中出现低频（delta）振荡时，它们往往在因子成分中占主导地位，这就导致分析delta频段以上的成分时就会有问题，再者，alpha振荡也干扰研究者感兴趣的4-7theta频段的振荡，导致因子数提取中太多非研究兴趣成分。解决的办法有三种：1）确保留下来的因子数能解释感兴趣频段的成分；2）滤掉不感兴趣的频段再做TF-PCA；3）不是直接滤波，而是限定时间窗，限制低频成分的方差贡献性。但是注意，以上三种方法都要视情况慎用。

2.2.4 时频平稳性的假设
TF-PCA的一个基本假设是TF的平稳性，即虽然单个成分的大小可能不同，但在很大程度上TF表征的总体“结构”保持相似。事实上，尽管单个因子的时间或频率响应的变化将导致因子在时间或频率维度上更分散，但TF-PCA的结果是比较稳健的。但如果研究目的是分析在不同条件下（即实验条件、评估时间点、样本组等）下比较这些成分的大小，那么在TF表征不一样的情况下去比较成分就困难了，因为不确定是否不同条件下明显的PCA加权的电压幅值差异是真正的幅值变化的结果，还是幅值中成分的组合变化和/或成分结构的变化条件。所以，在特定兴趣条件下，TF表征在成分结构中存在实质性差异，谨慎的做法是测试不同条件下基础成分结构的不变性，从而正确解释任何条件导致的差异。本文演示中应用了正交旋转，然后计算 Tuckers Φ作为脑电图数据的TF-PCA结构不变性的正式检验标准。当然也有一些其他的方法，本文不详细介绍，但建议的流程是：1）两两比较条件（比如实验条件、时间窗、群组等）中有一者为参考者；2）TF-PCA按上文介绍的流程对参考组进行；3）基于参考组提取的成分提取另一组数据；4）采用正交的曲线旋转，使加权矩阵从第二条件向参照组的加权矩阵旋转；5）计算Tuckers Φ度量跨两个条件下的结构不变性的。之前在其他领域的研究表明Φ>0.95反映了两种条件下的等效成分结构，0.95>Φ>0.85反映了中等水平的结构不变性，Φ<0.85反映了缺乏结构不变性。

3. 基于实例介绍TF-PCA方法在发展心理学的应用
TF-PCA在发展心理学研究中的应用意义包括：
1）检测被其他方法所遗漏的横断面差异。对FRN/RewP（反馈后负波/奖赏后正波）成分的研究，使用TF-PCA分析揭示了theta和delta 的TF-PCA因子得分与年龄相关的变化。此外，这些theta和delta因子分数与FRN/RewP具有相似的时间和地形，随后的回归分析显示了这些因子分数如何与FRN/RewP相关。利用TF-PCA可以提供跨年龄的神经认知变化的敏感指标，而该结果可能会被更传统的脑电图分析技术所忽略。
2）一种数据驱动的方法分离出感兴趣效应。在成年人中，错误试验中的反应（相对于正确的反应）与中额叶皮层的theta能力的增加有关，可以定义一个TF ROI，但在儿童中这个ROI就没有足够的支持性。此时可以使用TF-PCA方法，在成人近似时间、频带和地形依据下，识别该样本中与错误相关的中额theta TF-PCA成分，再分离出兴趣效应后，就能够进行推理和统计测试。
3）解开重叠的神经认知动力学。TF-PCA方法可用于分离相同TF表征中代表反应前theta（对刺激冲突更敏感）和反应后theta（对错误委员会更敏感）的不同成分，然后可以用于推测他们与刺激冲突，当前试验的准确性，和下一次试验的行为表现的关系。总的来说，TF-PCA可提供一个有用的框架来解开在单一TF表征中存在的特定子过程。
4）研究纵向变化。研究青少年不同时间点的脑电数据，先对后期时间点进行TF-PCA，以提取错误相关中额叶的theta的TF-PCA加权矩阵。然后，我们将该矩阵用于前后时间点数据进行TF表征计算，以便在每个时间点提取相同的错误相关的中额theta成分，之后就能统计这个错误相关的中额theta成分的纵向变化。此外，中额叶theta成分的发育变化也可以预测同一发育窗口内精神病理症状的纵向变化。但是，考虑之前所提的时频测量的平稳性问题，如果没有首先评估测量不变性，就不可能精确地推断观察到的变化是否反映了成分大小/结构的变化。因此，建议未来的工作尽可能完成测量不变性测试，以便得出更精确的结论。

4. 使用示例代码和数据的教程演练
本文最后的演练以及所有必需的数据、代码和生成的输出示例，可以在GitHub存储库：https://github.com/NDCLab/tfpca－教程中找到。

5. 结论
TF-PCA的独特价值在于提供了一种数据缩减方法，并且不依赖于关于感兴趣区域的特定时间或频率边界的先验知识约束，所以它也特别适合于发展心理学TF数据的分析。
参考文献：A practical introduction to EEG Time-Frequency Principal Components Analysis (TF-PCA)