39. 组合总和

题目

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。
示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都 互不相同
1 <= target <= 500

dfs思路一：

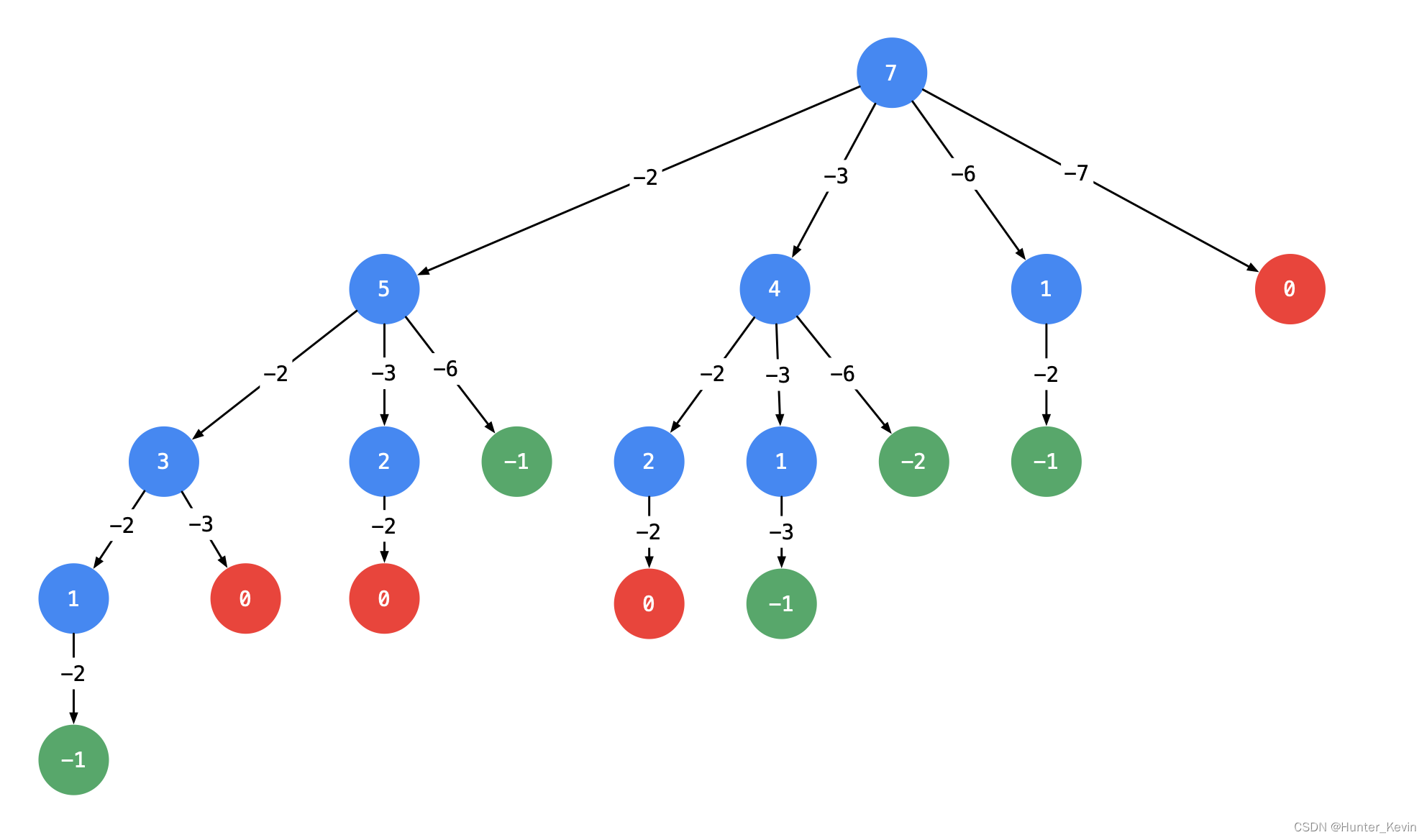
class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path; 
    vector<vector<int>> combinationSum(vector<int>& num, int target) {
        sort(num.begin(), num.end());
        dfs(num, 0, target);
        return ans;
    }

    void dfs(vector<int>& num, int begin, int target){
        // 如果符合情况，则添加到答案中
        if(target == 0){
            ans.push_back(path);
            return;
        }
        
        // 枚举当前下标之后的数字，去重
        for(int i = begin; i < num.size(); i++){
            // 如果减去当前位置元素之后剩余值<0时，则不再继续深搜,剪枝，递归结束的条件
            if(target - num[i] < 0) break;
            path.push_back(num[i]);
            dfs(num, i, target-num[i]);
            path.pop_back();
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

dfs思路二：

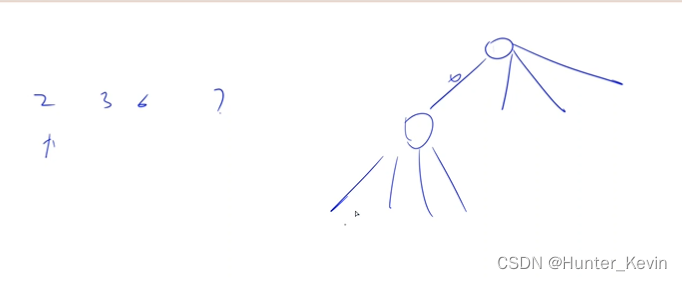
每一层表示num[cur]选几个
下一层表示num[cur+1]选几个
恢复现场的时候要清空当前层的状态，即当前层选了多少个，在结束之前就pop多少次

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    vector<vector<int>> combinationSum(vector<int>& num, int target) {
        dfs(num, target, 0);
        return ans;
    }

    void dfs(vector<int>& num, int target, int cur){
        // 如果符合条件，则添加到结果数组中
        if(target == 0){
            ans.push_back(path);
            return;
        }
        // 递归结束条件
        if(cur == num.size()) return;
        // 枚举在当前状态下，num[cur]选多少个，限制条件为在当前状态下，选取num[cur]的个数要<=剩余值
        for(int i = 0; i * num[cur] <= target; i++){
            dfs(num, target - i*num[cur], cur+1);
            path.push_back(num[cur]);
        }

        // 在当前状态下，num[cur]选取了多少个，就pop多少次，这里pop的是当前状态下的path
        for(int i = 0; i * num[cur] <= target; i++)
            path.pop_back();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28