【重温基础算法】内部排序之归并排序法

内部排序之归并排序法

归并排序（Merging sort）是建立在归并操作上的一种有效的排序算法。是采用分治法的一个非常典型的应用。

主要思想

2-路归并排序法

初始序列有n个元素记录，就可以看成$n$个子序列，每个子序列的长度为$1$，然后前后相邻的序列两两合并，得到$\lceil \frac{n}{2}\rceil$个长度为$2$或为$1$的有序子序列，在两两合并，直到得到一个长度为n的有序序列为止。

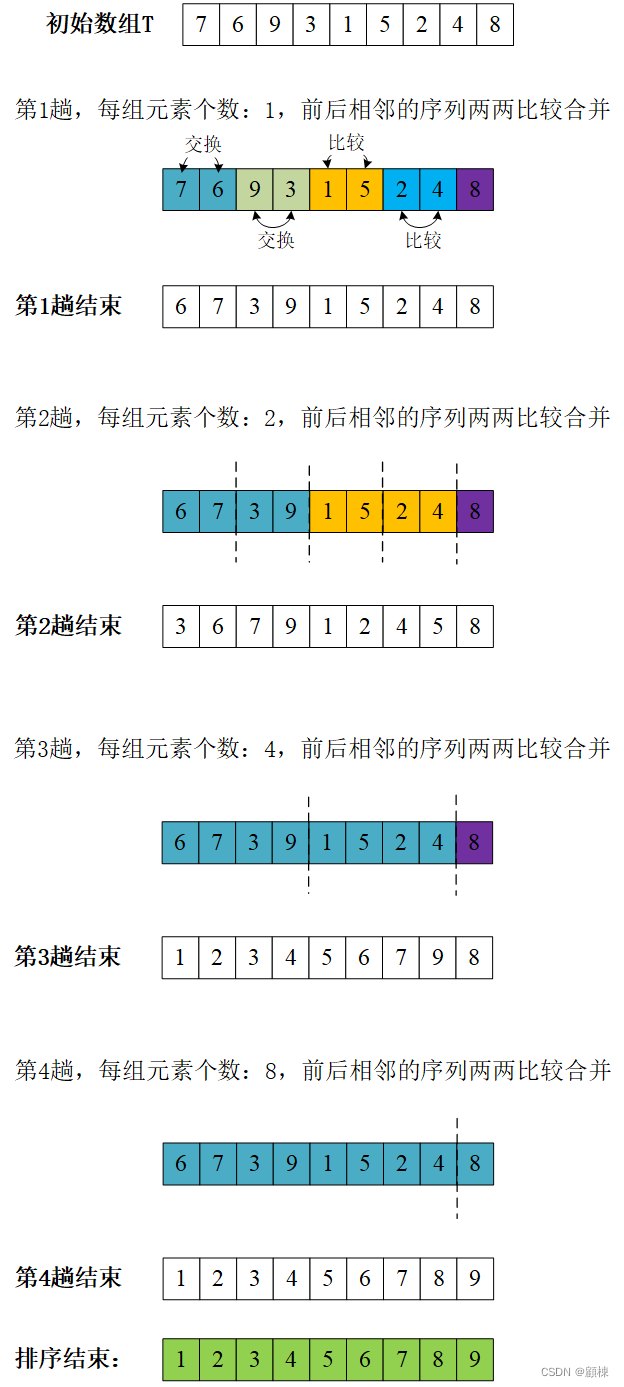
过程演示

递归过程

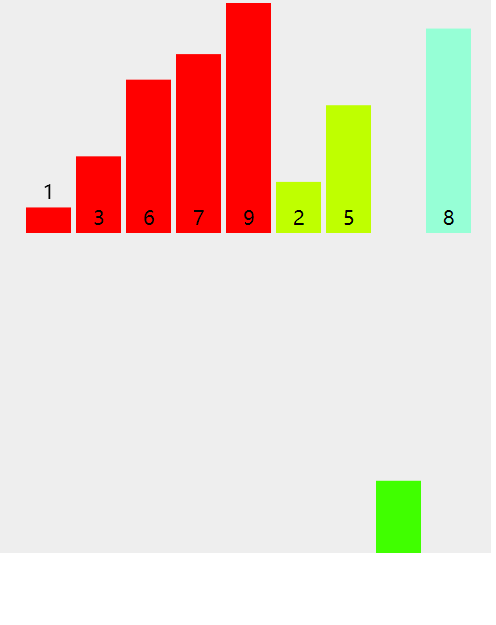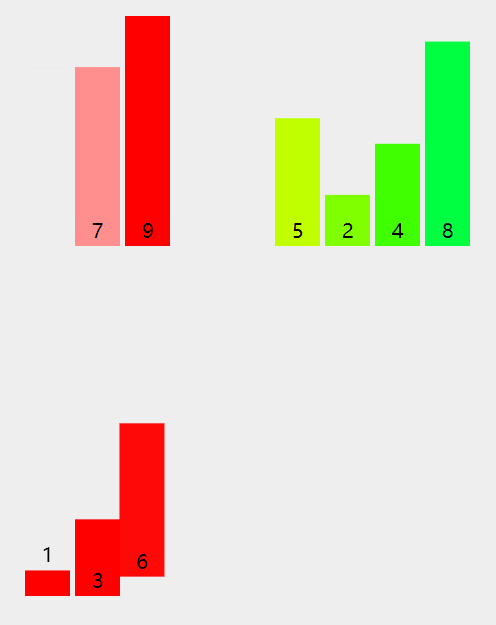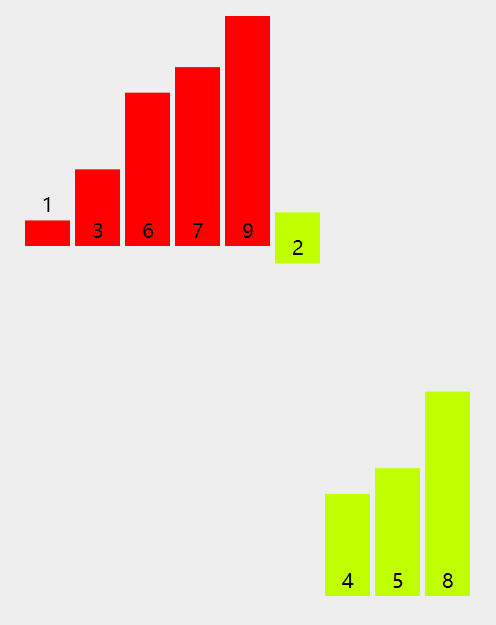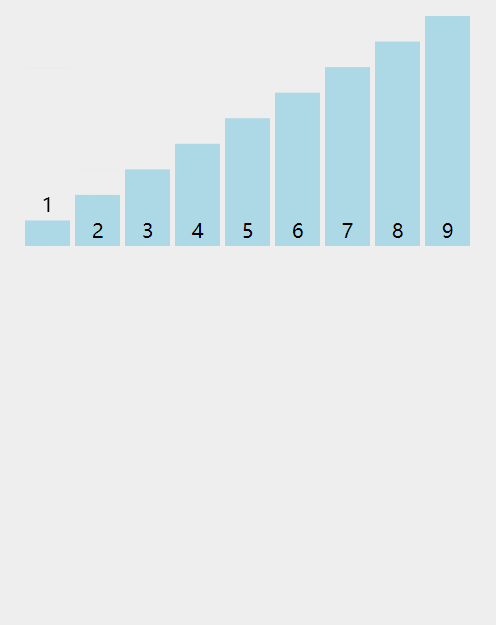
非递归过程

JAVA代码

非递归实现

package sort;

import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args) throws Exception {
        int[] o = {7, 6, 9, 3, 1, 5, 2, 4, 8};
        System.out.print("排序前: ");
        for (int t : o) {
            System.out.print(t);
            System.out.print(" ");
        }
        System.out.println();

        // 算法部分
        // 非递归的方式
        nonRecursive(o);

        System.out.print("排序后: ");
        for (int t : o) {
            System.out.print(t);
            System.out.print(" ");
        }
        System.out.println();

    }

    public static void nonRecursive(int[] o) {
        int[] temp = new int[o.length];
        int gap = 1;
        int count = 1;
        while (gap < o.length) {
            for (int i = 0; i < o.length; i = i + 2 * gap) {
                int j = i;
                // 比较的左数组
                int start1 = i;
                int end1 = i + gap - 1;
                // 比较的右数组
                int start2 = i + gap;
                int end2 = i + 2 * gap - 1;

                // 控制越界
                if (start2 >= o.length) {
                    break;
                }
                if (end2 >= o.length) {
                    end2 = o.length - 1;
                }

                while (start1 <= end1 && start2 <= end2) {
                    if (o[start1] > o[start2]) {
                        temp[j++] = o[start2++];
                    } else {
                        temp[j++] = o[start1++];
                    }
                }

                while (start1 <= end1) {
                    temp[j++] = o[start1++];
                }

                while (start2 <= end2) {
                    temp[j++] = o[start2++];
                }

                // 将本轮排序结果返回给o数组，
                if (end2 + 1 - i >= 0) {
                    System.arraycopy(temp, i, o, i, end2 + 1 - i);
                }

            }
            System.out.print("第" + count + "趟，每组元素个数：" + gap + "，排序后: ");
            for (int t : o) {
                System.out.print(t);
                System.out.print(" ");
            }
            System.out.println();
            count++;
            gap = 2 * gap;
        }
    }

    public static int[] sort(int[] sourceArray) {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        if (arr.length < 2) {
            return arr;
        }
        int middle = (int) Math.floor(arr.length / 2);

        int[] left = Arrays.copyOfRange(arr, 0, middle);
        int[] right = Arrays.copyOfRange(arr, middle, arr.length);

        return merge(sort(left), sort(right));
    }


    protected static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        int i = 0;
        while (left.length > 0 && right.length > 0) {
            if (left[0] <= right[0]) {
                result[i++] = left[0];
                left = Arrays.copyOfRange(left, 1, left.length);
            } else {
                result[i++] = right[0];
                right = Arrays.copyOfRange(right, 1, right.length);
            }
        }

        while (left.length > 0) {
            result[i++] = left[0];
            left = Arrays.copyOfRange(left, 1, left.length);
        }

        while (right.length > 0) {
            result[i++] = right[0];
            right = Arrays.copyOfRange(right, 1, right.length);
        }

        System.out.print("排序数组:");
        for (int t : result) {
            System.out.print(t);
            System.out.print(" ");
        }
        System.out.println();

        return result;
    }
}

结果

排序前: 7 6 9 3 1 5 2 4 8 
第1趟，每组元素个数：1，排序后: 6 7 3 9 1 5 2 4 8 
第2趟，每组元素个数：2，排序后: 3 6 7 9 1 2 4 5 8 
第3趟，每组元素个数：4，排序后: 1 2 3 4 5 6 7 9 8 
第4趟，每组元素个数：8，排序后: 1 2 3 4 5 6 7 8 9 
排序后: 1 2 3 4 5 6 7 8 9 

递归实现

package sort;

import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args) throws Exception {
        int[] o = {7, 6, 9, 3, 1, 5, 2, 4, 8};
        System.out.print("排序前: ");
        for (int t : o) {
            System.out.print(t);
            System.out.print(" ");
        }
        System.out.println();

        // 算法部分
        // 递归的方式
        o = sort(o);

        System.out.print("排序后: ");
        for (int t : o) {
            System.out.print(t);
            System.out.print(" ");
        }
        System.out.println();

    }

    public static void nonRecursive(int[] o) {
        int[] temp = new int[o.length];
        int gap = 1;
        int count = 1;
        while (gap < o.length) {
            for (int i = 0; i < o.length; i = i + 2 * gap) {
                int j = i;
                // 比较的左数组
                int start1 = i;
                int end1 = i + gap - 1;
                // 比较的右数组
                int start2 = i + gap;
                int end2 = i + 2 * gap - 1;

                // 控制越界
                if (start2 >= o.length) {
                    break;
                }
                if (end2 >= o.length) {
                    end2 = o.length - 1;
                }

                while (start1 <= end1 && start2 <= end2) {
                    if (o[start1] > o[start2]) {
                        temp[j++] = o[start2++];
                    } else {
                        temp[j++] = o[start1++];
                    }
                }

                while (start1 <= end1) {
                    temp[j++] = o[start1++];
                }

                while (start2 <= end2) {
                    temp[j++] = o[start2++];
                }

                // 将本轮排序结果返回给o数组，
                if (end2 + 1 - i >= 0) {
                    System.arraycopy(temp, i, o, i, end2 + 1 - i);
                }

            }
            System.out.print("第" + count + "趟，每组元素个数：" + gap + "，排序后: ");
            for (int t : o) {
                System.out.print(t);
                System.out.print(" ");
            }
            System.out.println();
            count++;
            gap = 2 * gap;
        }
    }

    public static int[] sort(int[] sourceArray) {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        if (arr.length < 2) {
            return arr;
        }
        int middle = (int) Math.floor(arr.length / 2);

        int[] left = Arrays.copyOfRange(arr, 0, middle);
        int[] right = Arrays.copyOfRange(arr, middle, arr.length);

        return merge(sort(left), sort(right));
    }


    protected static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        int i = 0;
        while (left.length > 0 && right.length > 0) {
            if (left[0] <= right[0]) {
                result[i++] = left[0];
                left = Arrays.copyOfRange(left, 1, left.length);
            } else {
                result[i++] = right[0];
                right = Arrays.copyOfRange(right, 1, right.length);
            }
        }

        while (left.length > 0) {
            result[i++] = left[0];
            left = Arrays.copyOfRange(left, 1, left.length);
        }

        while (right.length > 0) {
            result[i++] = right[0];
            right = Arrays.copyOfRange(right, 1, right.length);
        }

        System.out.print("排序数组:");
        for (int t : result) {
            System.out.print(t);
            System.out.print(" ");
        }
        System.out.println();

        return result;
    }
}

结果

排序前: 7 6 9 3 1 5 2 4 8 
排序数组:6 7 
排序数组:3 9 
排序数组:3 6 7 9 
排序数组:1 5 
排序数组:4 8 
排序数组:2 4 8 
排序数组:1 2 4 5 8 
排序数组:1 2 3 4 5 6 7 8 9 
排序后: 1 2 3 4 5 6 7 8 9 

算法分析

时间复杂度

对n个元素的序列进行归并排序，若$n>1$，T(n)=本次分组的合并时间加上，拆分成两个小组的比较合并时间，若$n=1$,即有序了。所花时间可能就是一个常数C。则
T ( n ) = { C n = 1 n + 2 T ( n 2 ) n > 1 T(n)=

T(n)={C​n+2T(2n​)​n=1n>1​

∴ T ( n ) = n + 2 T ( n 2 ) = n + 2 ( n 2 + 2 T ( n 4 ) ) = 2 n + 4 T ( n 4 ) = n + 2 ( n 2 + 2 ( n 4 + 2 T ( n 8 ) ) ) = 3 n + 8 T ( n 8 ) . . . = k n + 2 k ∗ T ( n 2 k ) 当 n 2 k = 1 时，分组达到最后一层，即 k = l o g 2 n 原式 = n ∗ l o g 2 n + 2 l o g 2 n ∗ C = n l o g 2 n + C ∗ N    ⟹    O ( n l o g 2 n )

∴T(n)当2kn​原式​=n+2T(2n​)=n+2(2n​+2T(4n​))=2n+4T(4n​)=n+2(2n​+2(4n​+2T(8n​)))=3n+8T(8n​)...=kn+2k∗T(2kn​)=1时，分组达到最后一层，即k=log2n​=n∗log2n​+2log2n​∗C=nlog2n​+C∗N⟹O(nlog2n​)​​

由于归并排序的算法跟有序度无关，所以时间复杂度很稳定都是$O(nlo{g}_2^n)$；

空间复杂度

在算法实现中，需要申请与长度不超过$n$的空间使用。其空间复杂度为$O(n)$。