-
树状数组实战
一 问题提出
一个包含 n 个数的序列2,7,1,12,5,9...,计算前 i 个数的和值,即前缀和 sum[i|=a[1]+a[2]+…+a[i]。该怎么计算呢?
累加求前 n 个数的和值需要 O(n)时间。而且若对 a[i] 进行修改,则sum[i],sum[i+1 ],...sum[n] 都需要修改,最坏的情况下需要 O(n) 时间。
树状数组可以高效实现,其查询前缀和与点更新均为O(logn)。
二 树状数组原理
树状数组引入了分级管理制度,设置一个管理小组,每个管理员管理一个或多个连续的元素。例如,数列有9个元素,分别用a[1],a[2],…,a[9] 存储,管理数组为 c[]。管理数组 c[] 是树状的,因此称为树状数组。
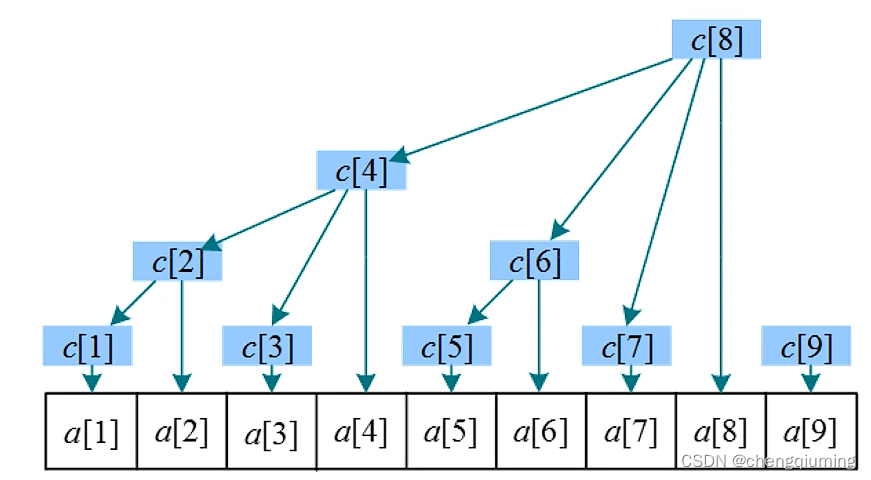
树状数组,又称为二进制索引树(Binary Indexed Trees ),通过二进制分解划分区间。那么 c[i]存储的是哪些值?
1 区间长度
若 i 的二进制表示末尾有 k 个连续的 0,则 c[i] 存储的区间长度为2^k,从 a[i]向前数 2^k 个元素,即 c[i] = a[i-2^k+1]+a[i-2^k+2]+...a[i]。
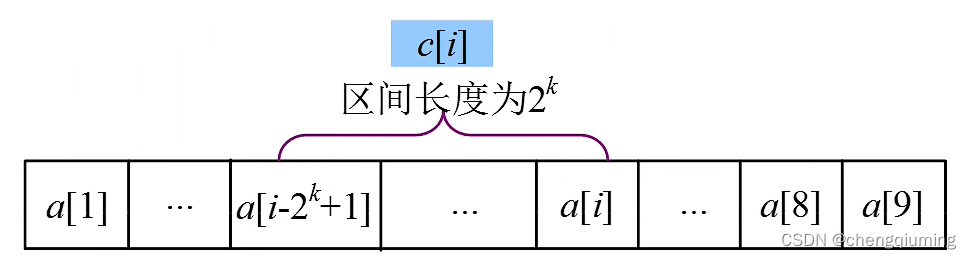
区间长度就是 i 的二进制表示下最低位的 1 及它后面的 0 构成的数值。例如 i=20,其二进制表示为10100,末尾有2个0,区间长度为2^2,其实就是 10100 最低位的 1 及其后面的 0 构成的二进制数值 100,十进制为 4。
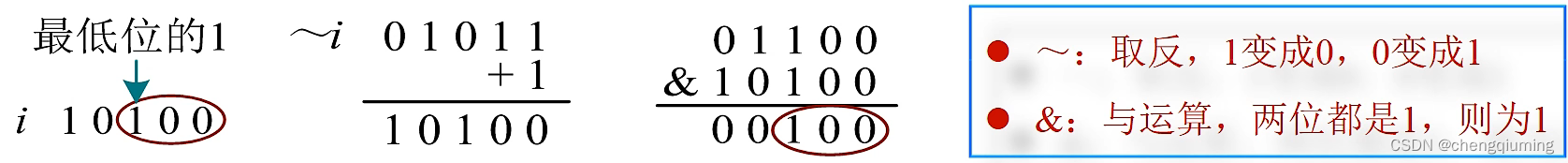
在计算机中二进制数采用的是补码表示,-i 的补码正好是 i 取反加1。
c[i] 存储的区间长度:lowbit(i)=(-i)&i
2 前驱和后继
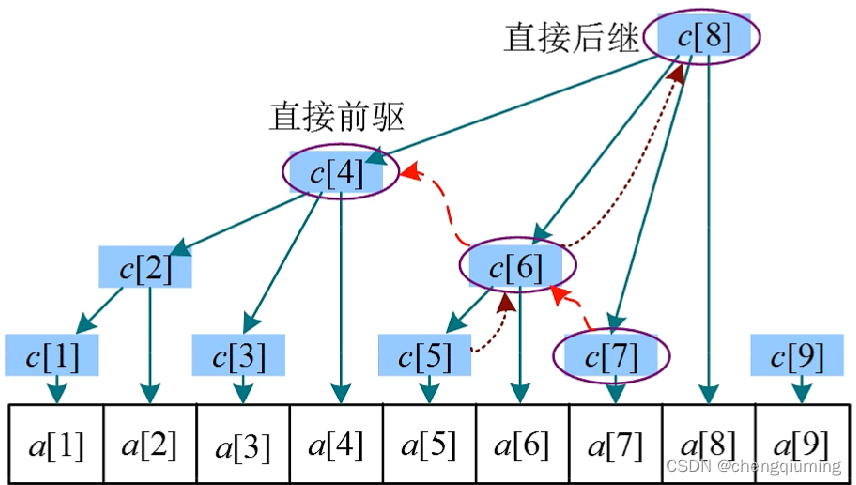
直接前驱:c[i] 的直接前驱为 c[i-lowbit(i)],即 c[i] 左侧紧邻的子树的根。
直接后继:c[i] 的直接后继为 c[i+lowbit(i)],即 c[i] 的父节点。
前驱:c[i] 左侧所有子树的根。
后继:c[i] 的所有祖先。
3 查询前缀和
前 i 个元素的前缀和 sum[i] 等于 c[i]+c[i]的前驱。
sum[7] 等于 c[7] 加上 c[7] 的前驱,sum[7]=c[7]+c[6]+c[4]。
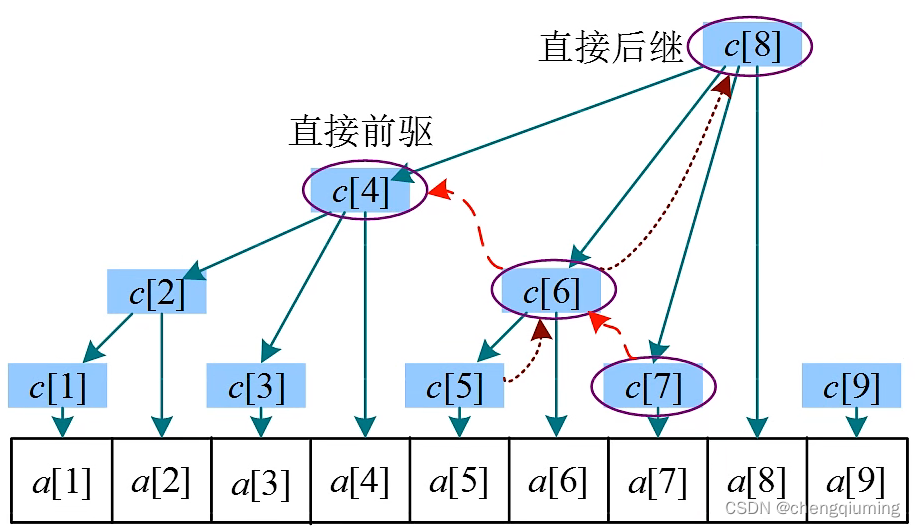
4 点更新
若对 a[i] 进行修改,令 a[i] 加上一个数 z,则只需更新 c[i] 及其后继(祖先),即令这些节点都加上 z 即可,无需修改其他节点。
例如,修改 a[5],令其加2。
只需 c[5]+2,然后c[5]的后继分别加2,即c[6]+2、c[8]+2。
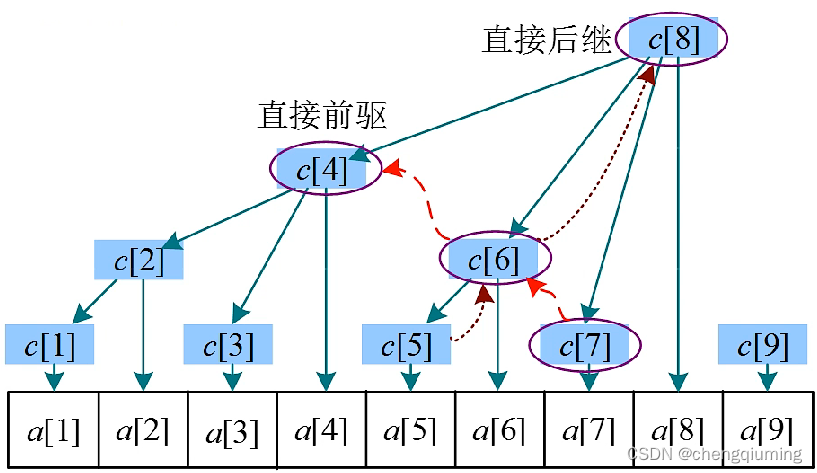
5 查询区间和
若求区间和值 a[i]+a[i+1]+...+a[j],则求解前 j 个元素的和值减去前 i-1 个元素的和值即可,即sum[j]-sum[i-l ]。
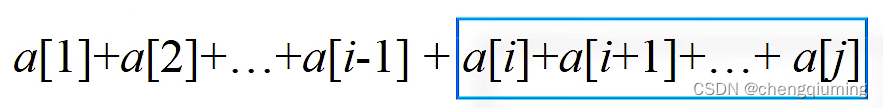
三 代码
- package com.platform.modules.alg.alglib.p65;
- public class P65 {
- private final int maxn = 10000;
- int n;
- int a[] = new int[maxn];
- int c[] = new int[maxn];
- int s[] = new int[maxn];
- public String output = "";
- // c[i]的区间长度
- int lowbit(int i) {
- return (-i) & i;
- }
- // a[i]加上z
- void add(int i, int z) {
- for (; i <= n; i += lowbit(i)) // 直接后继,即父亲i+=lowbit(i)
- c[i] += z;
- }
- // 求前缀和a[1]..a[i]
- int sum(int i) {
- int s = 0;
- for (; i > 0; i -= lowbit(i)) // 直接前驱 i-=lowbit(i);
- s += c[i];
- return s;
- }
- // 求区间和a[i]..a[j]
- int sum(int i, int j) {
- return sum(j) - sum(i - 1);
- }
- public String cal(String input) {
- String[] line = input.split("\n");
- n = Integer.parseInt(line[0]);
- String[] num = line[1].split(" ");
- for (int i = 1; i <= n; i++) {
- a[i] = Integer.parseInt(num[i - 1]);
- add(i, a[i]);//加入树状数组
- }
- int x1, x2;
- String[] query = line[2].split(" ");
- x1 = Integer.parseInt(query[0]);
- x2 = Integer.parseInt(query[1]);
- output += sum(x1) + "\n";
- output += sum(x1, x2) + "";
- return output;
- }
- }
四 测试
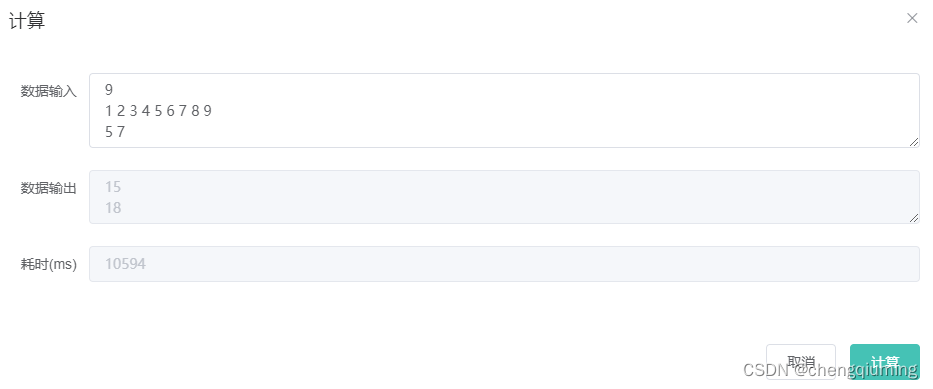
-
相关阅读:
Git使用及配置
07-app端文章搜索-黑马头条
浅尝docker--基础篇
vivo 基于 JaCoCo 的测试覆盖率设计与实践
23年用vuex进行状态管理out了,都开始用pinia啦!
二分搜索树深度优先遍历(Java 实例代码)
Spring-Cloud-Alibaba-SEATA源码解析(二)(客户端)
Go+VsCode配置环境
GoFrame:如何简单地搭建一个简单地微服务
从压测碰到的诡异断连问题聊聊Nginx的连接管理
- 原文地址:https://blog.csdn.net/chengqiuming/article/details/126941750