孟桥版信号与系统学习笔记

第三章开篇语

信号与系统必须要啃下来，不能只停留老师的讲课视频上，必须要运用到实践中。对于已经学过的章节特意做一个归纳总结，当笔记使用。因为刚把第三章，连续信号的正交分解 学习了，所以先从此章开始。

线性系统的分析方法最根本的是应用了线性系统的齐次性和叠加性。这样我们可以把复杂的激励信号分解为很多个简单的激励信号的和，这里的和是广义的求和，是积分。然后我们通过简单信号的响应，把他们加到一起，我们就可以得到复杂信号的响应。在第二章中，我们把响应分为0输入响应和0状态响应，我们更关注的是0状态响应，因为我们更关心的是说，把信号加到系统上以后系统有什么反应，0输入响应是自然产生的，一方面我们不是太关心，第二个很多系统搭起来后給其上电也不可能有什么初始储能。所以相对来说，我们对零状态响应更为关心。
零状态响应带来的东西比较多，激励信号可能会千变万化比较复杂，第二个就是我应对的系统可能会比较复杂。这个时候就需要进行简化。复杂信号变为简单信号的和，其实对系统的简化也是如此，給的高阶系统，可以变成很多个低阶系统的和（通过部分分式分解进行变化）。
低阶系统的冲激响应是容易求的，把各个低阶系统冲激响应加到一起就是那个高阶系统的冲激响应。

那么我们需要做的工作有：
选子信号：找什么样的子信号？
如何分解：怎么样把任何的一个复杂信号分解为子信号的和？
子信号响应：如何求解子信号的响应？
如何叠加：如何把很多个子信号的响应叠加成整个信号的响应？怎么合成为一个统一的公式。

对于第二章，
选子信号选的是冲激信号或阶跃信号；
分解是通过卷积积分的形式进行分解，把复杂信号变成很多个冲激信号或阶跃信号的和（其实我们看到的是积分，广义上的求和）；
子信号的响应，我们进行了冲激信号的求解过程；
最后叠加就是个卷积公式e(t)卷积h（t）;

不过第二章的这种做法不是唯一的，子信号的选法并不是唯一的只可以选取冲激或者阶跃。第三章我们选取的子信号是正选信号函数。我们想办法把一个任意信号分解为很多个正弦信号的和，然后通过系统对正弦信号的响应，来求解系统对任意一个信号的响应。

这种做法在工程当中，比第二章中的时域法更有意义，他能带出很多相应的概念，比如说信号的频域特性，系统的频域特性等等。很多时候，用频域来研究解决一个问题要比时域法要简洁的多，而且可以得到很多非常具有实用价值的一般性结论，这些一般性结论可以給在以后的研究或者设计当中带来很多很多好处。

现在从新来回答一遍问题，
选什么样的子信号：选正弦信号；
怎么样分解：怎么样把任意一个信号分解为一系列正弦信号的和或者积分；
怎么样求子信号的响应，其实这个子信号的响应我们见过，在电路分析课程中，有讲解电路的正弦稳态响应；
如何叠加，一样的，如何合成系统对整个激励的响应。

对于本章就是要研究如何对信号进行分解与合成

俩函数的分量系数

这里系数C12的选择，要求使误差函数的方均值为最小。误差函数的方均值为







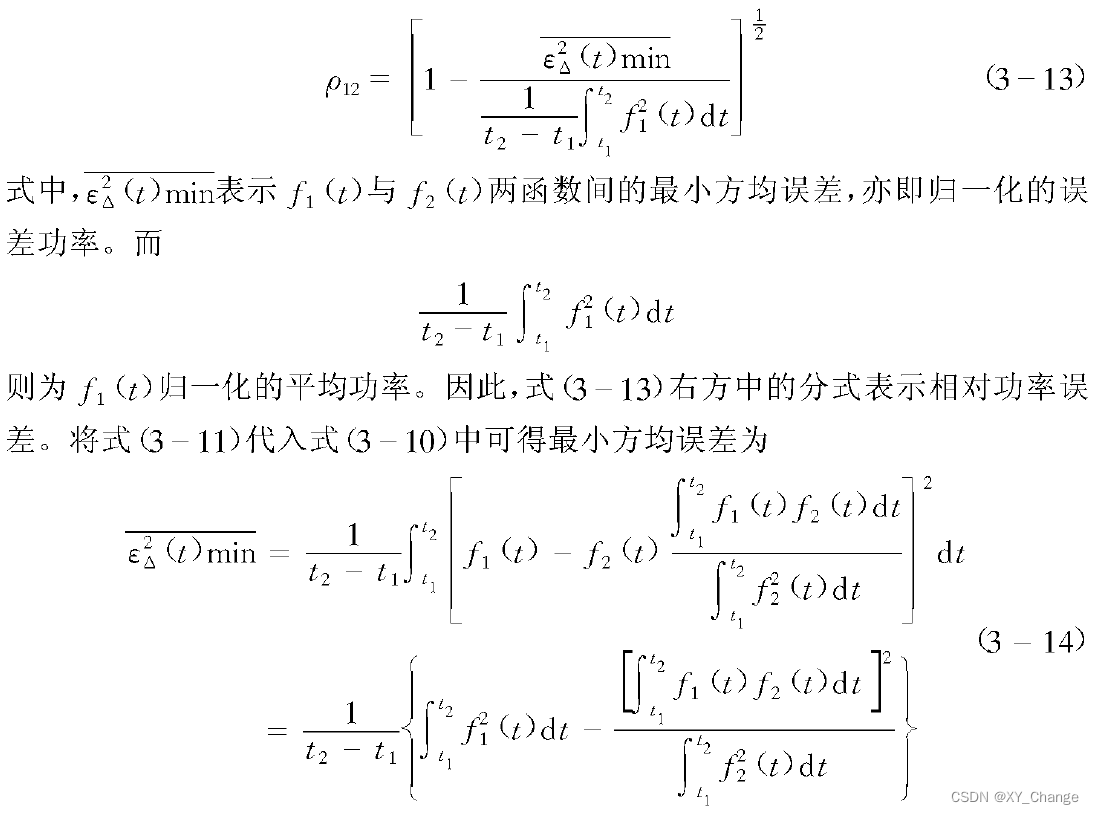
总结以上，与矢量分解相似，对信号进行分解。
单个标准信号下的分解



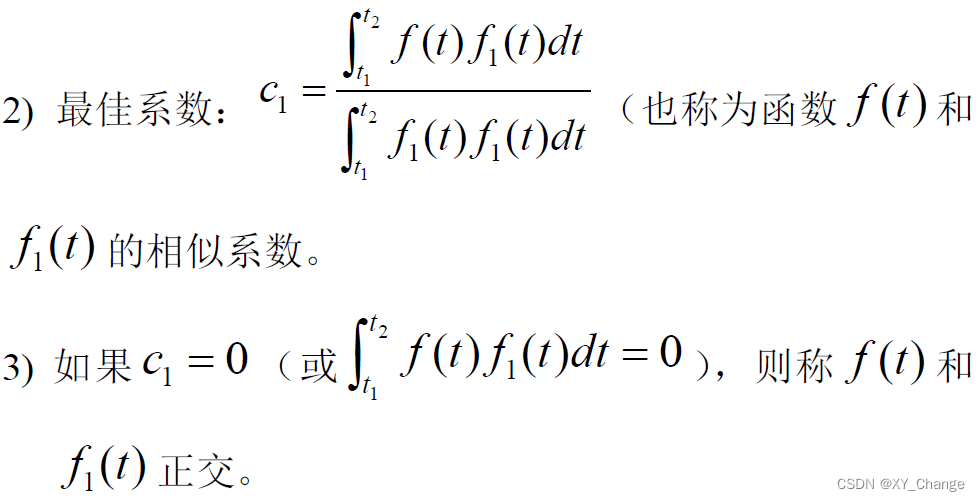
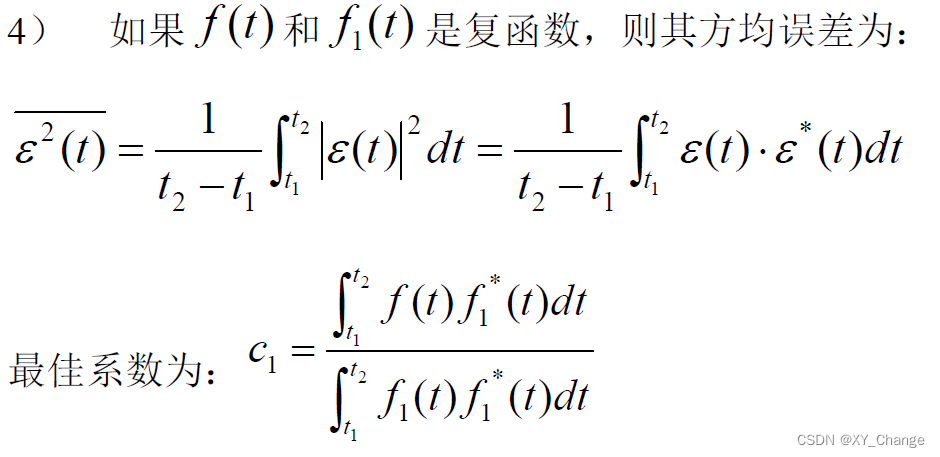
方均误差其实就是误差信号的平均功率。

信号的傅里叶级数表示

所用函数集：

需要证明函数集是否满足正交性

再看看是否是归一化的

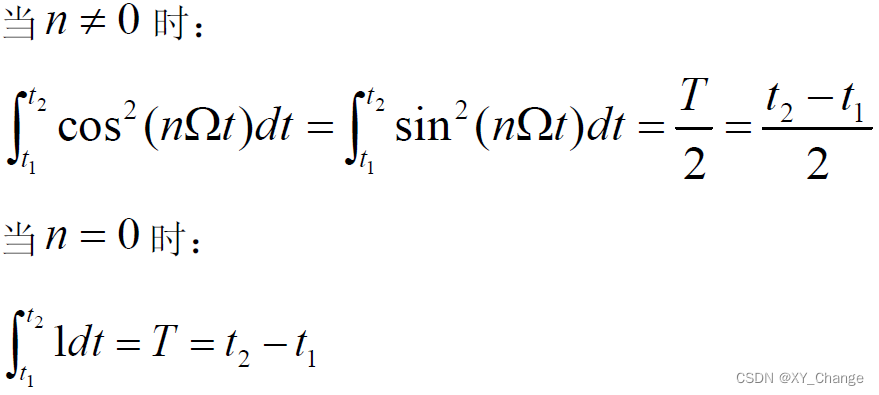
由此看是不归一的，不归一就不归一，算时注意一下就行，正交必须满足就行。




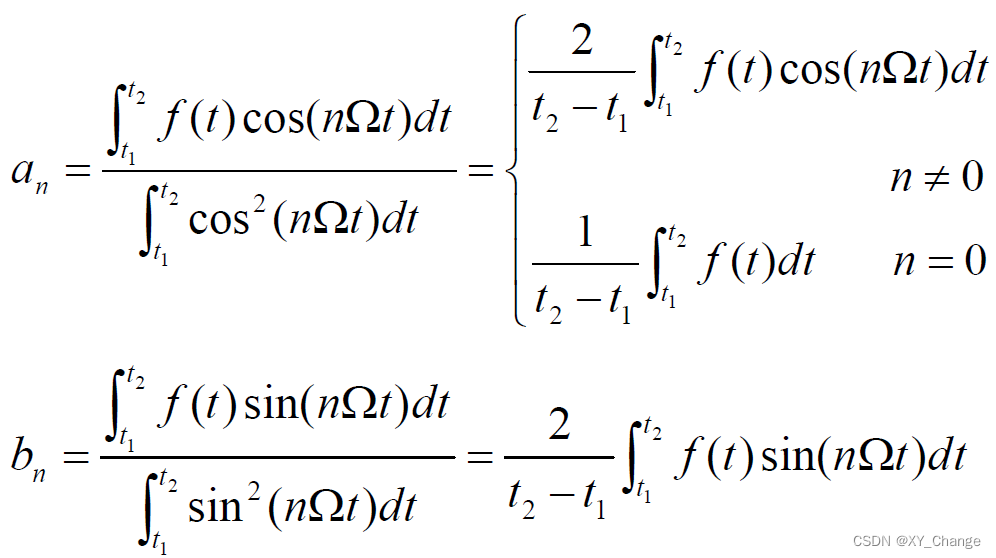
对于求解线性时不变系统的响应，激励信号平移了以后，响应信号也会平移。

对于上面的分解等式左右两边函数是否相等，没有误差？或者，是否随着n趋向于无穷大，等式右边的函数收敛于左边的函数？迪利克雷回答了此问题


第三种展开-----将函数用复指数正交函数集展开

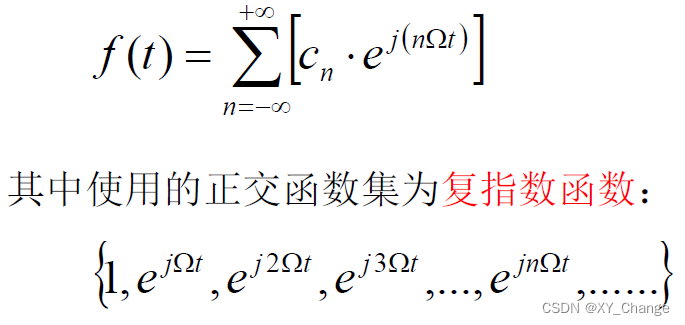
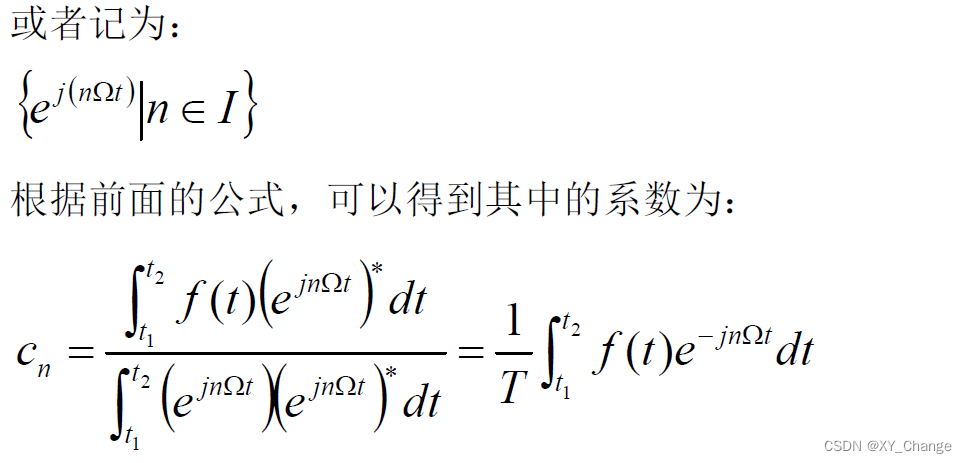
复指数形式的傅里叶级数推导从三角函数形式的傅里叶级数入手

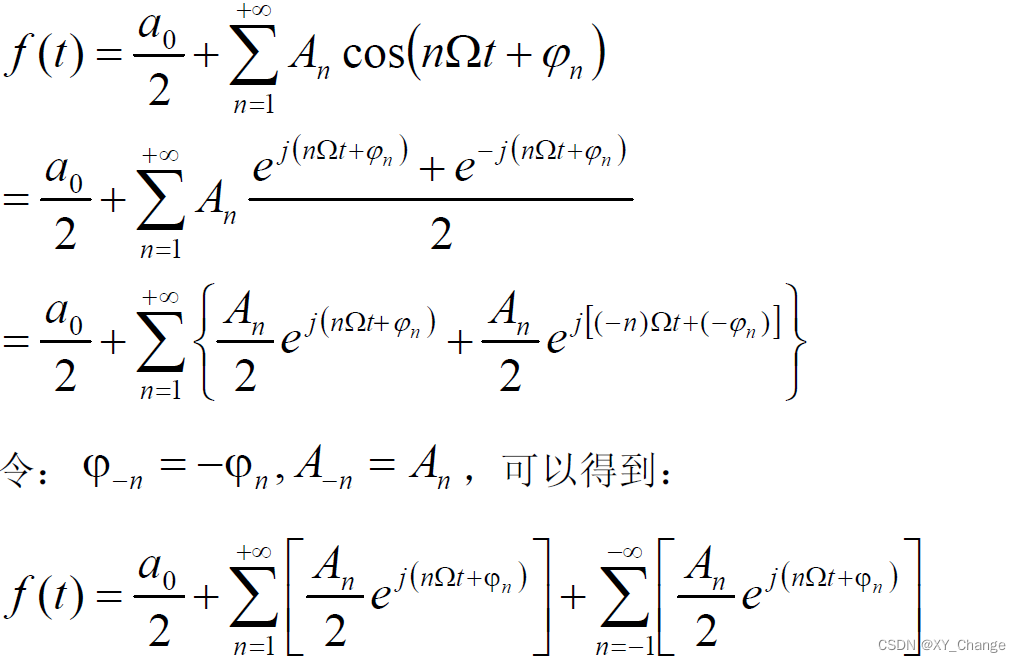
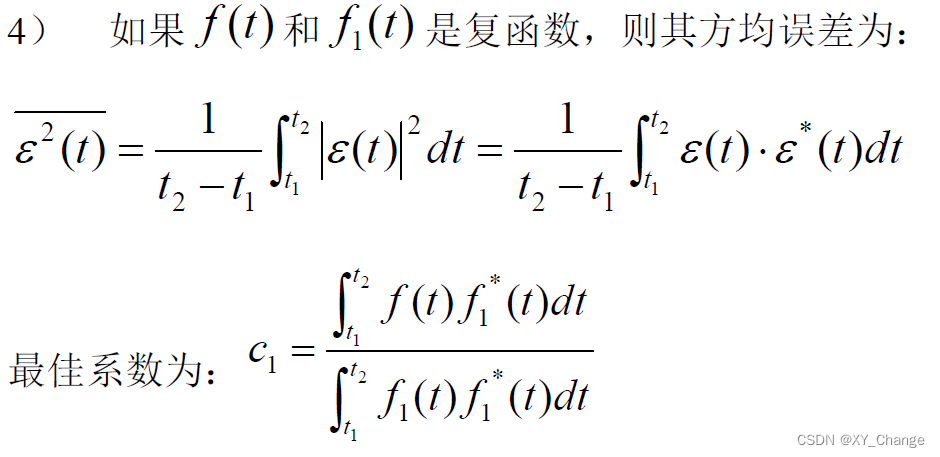
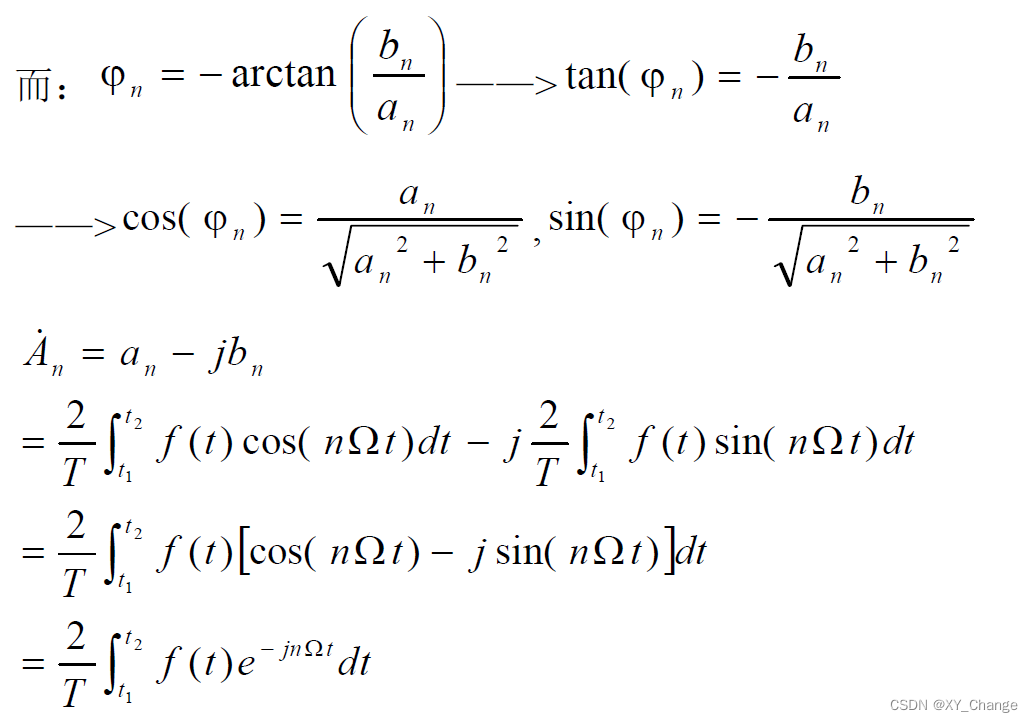
三种形式的傅里叶展开式：一种是sin、cos的；第二种是就是按照cos的；第三种是复指数的。

通过函数的奇偶谐波特性，可以使我们对傅里叶级数中包含的成份进行快速判断，有利于我们的计算。


在用有限项的傅里叶级数去逼近一个信号的时候，这个信号的功率差（少算的功率）就等于逼近的方均误差。