leetcode 101对称二叉树

对称二叉树

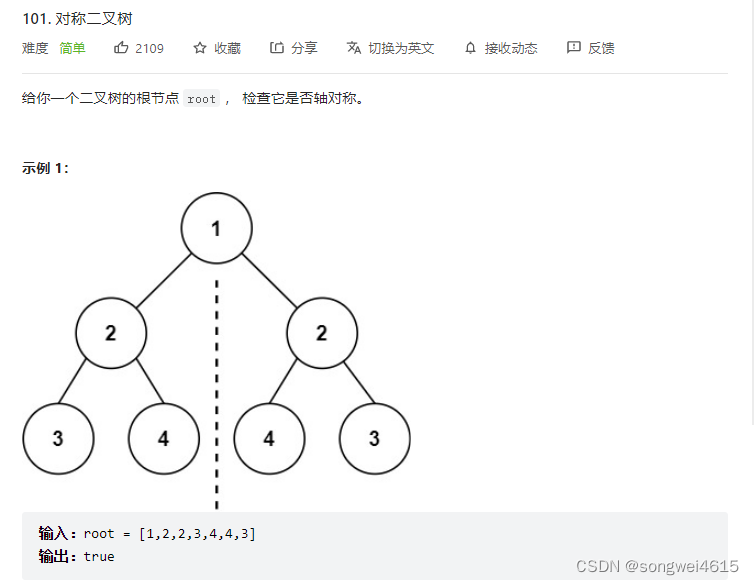
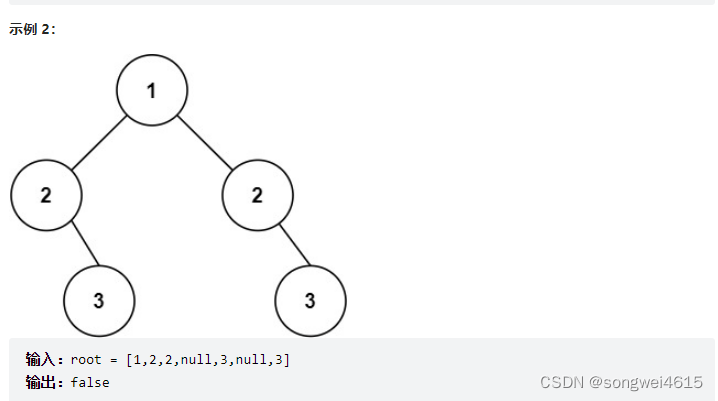
对称二叉树核心是对比左子树和右子树是否对称。
即 外侧 左子树的左和右子树的右 ；
内侧 左子树的右和右子树的左

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool compare(TreeNode* cur_left ,TreeNode* cur_right)
    {
    	//左子树和右子树都是空的，说明是叶子节点，对称
        if(cur_left == nullptr && cur_right == nullptr ) return 1;
        //左子树是空，右子树有值，不对称
        else if(cur_left ==nullptr && cur_right != nullptr) return 0;
        //左子树有值，右子树为空，不对称
        else if(cur_left !=nullptr && cur_right == nullptr) return 0;
        //左右子树内容不相等，不对称
        else if(cur_left->val != cur_right->val) return 0;
		
		//递归计算外侧和内侧的是否对称
        bool outside = compare(cur_left->left , cur_right->right);
        bool inside =  compare(cur_left->right , cur_right->left);
		//内测外侧都对称，则树对称
        return outside&&inside;

    }
    bool isSymmetric(TreeNode* root) {
		//如果是空节点，返回对称
        if(root ==nullptr) return 1;
        //递归对比左子树和右子树
        return compare(root->left , root->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

二刷

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool back_track(TreeNode* left_tree , TreeNode* right_tree )
    {
        if(left_tree == nullptr && right_tree == nullptr ) return true;
        else if(left_tree == nullptr || right_tree == nullptr ) return false;
        else if(left_tree->val != right_tree->val) return false;

        bool inside = back_track(left_tree->right , right_tree->left);
        bool outside = back_track(left_tree->left , right_tree->right);

        return inside&outside;
    }
    bool isSymmetric(TreeNode* root) {
       
        if(root==nullptr) return true;
        return back_track(root->left , root->right);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

高刷题

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool result = true;
    void track_back(TreeNode* cur1 , TreeNode* cur2)
    {
        if(cur1 == nullptr && cur2 == nullptr) return;
        if(cur1 == nullptr || cur2 == nullptr)
        {
            if(result == true) result = false;
            return;
        }

        if(cur1->val != cur2->val && result == true) result = false;

        track_back(cur1->left,cur2->right);
        track_back(cur1->right,cur2->left);
        return;
    }
    bool isSymmetric(TreeNode* root) {
        track_back(root->left , root->right);
        return result;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34