算法入门之链表简介

链表简介

前言

链表为数据结构中第二种基本结构，一般链表就是指在物理结构上非连续，非有序的数据结构，链表又分为单向链表和双向链表，单向链表一般可以如下定义

class Node{
    // 链表节点存放数字
    int data;

    // 节点的后指针
    Node next;
}

1
2
3
4
5
6
7
8

结构图如下

因为单向链表搜索顺序只能由左到右，显然对检索效率有一定影响，这时候就要推出双向链表，顾名思义就是在单项链表的基础上新增一个prev前指针既可以向前搜索也可以向后搜索，定义如下

class Node1{
    // 链表节点存放数字
    int data;

    // 节点的后指针
    Node next;

    // 节点的前指针
    Node prev;
}

1
2
3
4
5
6
7
8
9
10
11

结构图如下

链表的基本操作

为实现方便下面代码采用单项链表

链表插入操作

链表插入和数组插入同样需要考虑如下的问题

队头插入

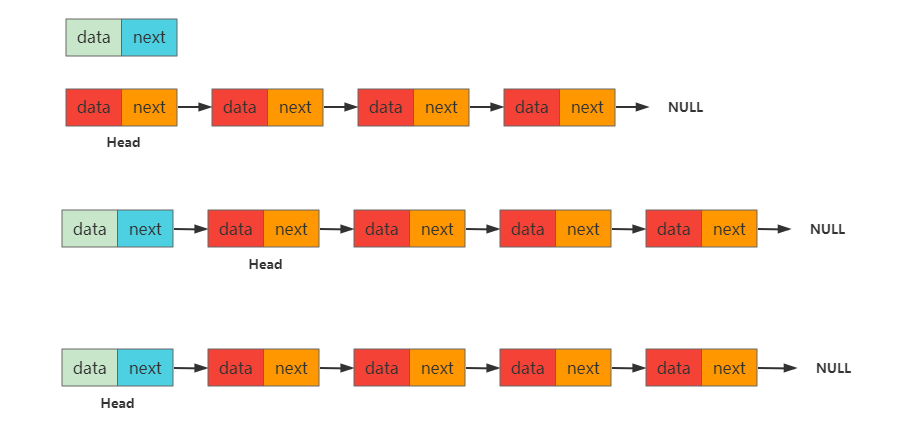
将一个新的Node节点从链表的头部插入，注意这里不用像数组一样还需要移动其它元素，这个过程分为两步

• 将新的Node节点的next指针指向原Head头节点。

• 链表Head头节点指向新Node节点。

队尾插入

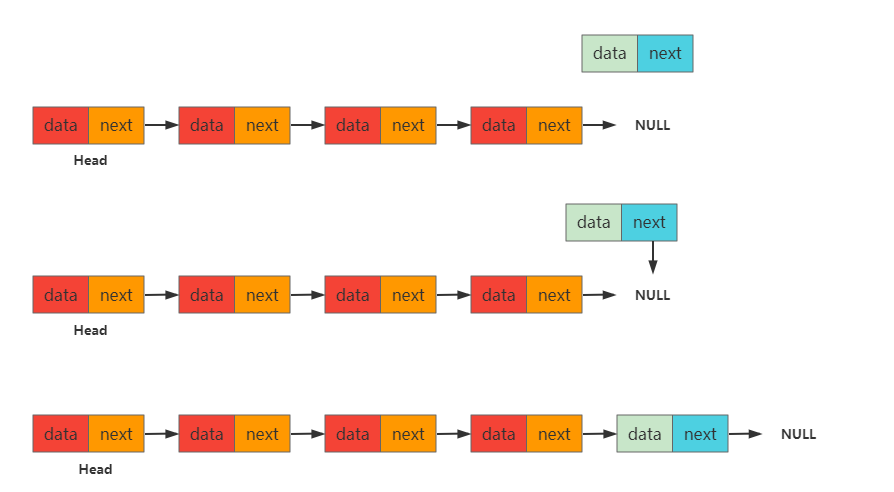
队尾插入和队头插入类似，同样分为两步

• 将新的Node节点next指针置为NULL。

• 将原队尾节点的next指针指向新的Node节点

中间插入

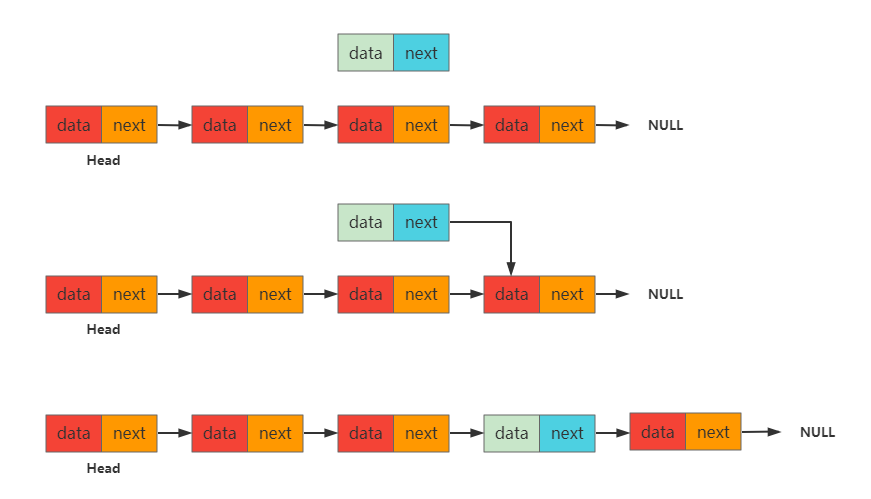
中间插入和其余两种完全不同，这个过程分为三个步骤

• 获取插入位置的前一个元素，因为链表是单向的，直接获取插入位置元素后将无法获取插入位置前的元素。

• 将新Node节点的next指针指向需要插入的位置。

• 将插入位置的前一个元素的next指针指向新的Node节点，形成链表。

按照这个思路整理代码如下

public class LinkedDemo {
    /**
     * 定义单向链表节点
     */
    private static class Node{
        // 链表节点存放数字
        int data;

        // 链表的下一个节点
        Node next;

        public Node(int data){
            this.data = data;
            this.next = null;
        }

        @Override
        public String toString() {
            return "Node{" +
                    "data=" + data +
                    ", next=" + next +
                    '}';
        }
    }

    // 头指针
    private Node head;

    // 尾指针（为了尾部插入方便）
    private Node last;

    // 链表长度
    private int size;

    /**
     * 链表插入
     * @param index
     * @param date
     */
    public void insert(int index,int date){
        if (index < 0 || index > size){
            throw new RuntimeException("下标值有误");
        }

        Node insertData = new Node(date);

        if (size == 0){
            // 空链表
            head = insertData;
            last = insertData;
        } else if (index == 0){
            // 队头插入
            insertData.next = head;
            head = insertData;
        }else if(index == size){
            // 队尾插入
            last.next = insertData;
            last = insertData;
        }else {
            // 链表中间插入
            // 先要去获取index下标的前一个Node节点（注意不是index下标的节点）
            Node indexNode = getIndexNode(index-1);

            insertData.next = indexNode.next;
            indexNode.next = insertData;
        }
        size++;
    }

    public void show(){
        Node temp = head;
        do {
            System.out.println(temp.toString());
            temp = temp.next;
        }while (temp!=null);
    }

    /**
     * 获取执行下标的Node节点
     * @param index 下标应该位于[0,size)之间
     * @return
     */
    public Node getIndexNode(int index){
        Node temp = head;
        for (int i = 0; i < index ; i++) {
            temp = temp.next;
        }
        return temp;
    }

    public static void main(String[] args) {
        LinkedDemo linkedDemo = new LinkedDemo();
        linkedDemo.insert(0,12);
        linkedDemo.insert(1,33);
        linkedDemo.insert(2,45);
        linkedDemo.insert(3,3);

        linkedDemo.insert(0,999);

        linkedDemo.show();
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103

链表删除操作

理解了链表的插入操作，链表的删除操作也是类似了，同样分为三种方式

队头删除

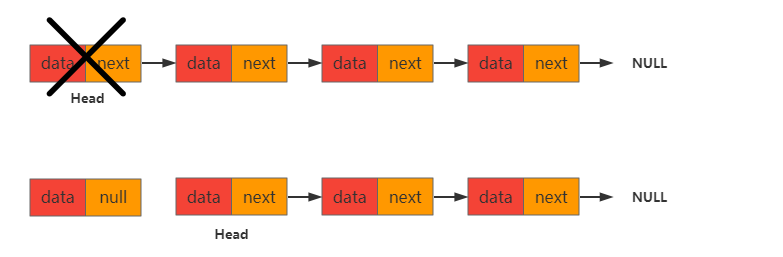
队头节点就是head，那么删除步骤分为

• 获取队头节点的下一个节点newHead。

• 将原对头节点的next指针置为NULL，对于JAVA语言对象回收由GC处理，所以只需要让Node对象无引用即可。

• 将head头节点指向原头节点的下一个节点newHead。

队尾删除

队尾删除的关键就是获取队尾的前一个节点，将队尾的前一个节点的next指针置为NULL即可。

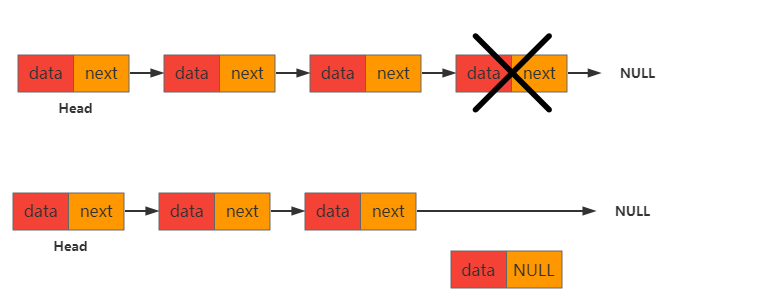
中间删除

中间删除较为复杂分为如下几步

• 获取删除元素的前一个节点和后一个节点。

• 将删除元素的next指向指向NULL。

• 将删除元素的前一个节点指向删除元素的后一个节点。

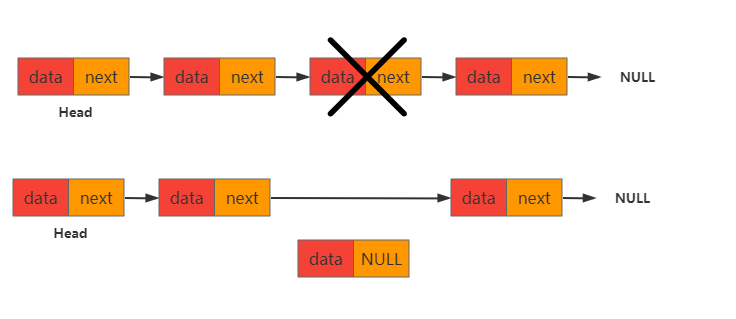
综上删除代码如下

    /**
     * 删除元素
     */
    public void delete(int index){
        if (index < 0 || index >= size){
            throw new RuntimeException("下标值有误");
        }

        if (index == 0){
            // 队头删除
            Node next = head.next;
            head.next = null;
            head = next;
        }else if (index == size){
            // 队尾删除
            // 获取队尾的前一个节点
            Node node = getIndexNode(index - 1);
            last = node;
        }else {
            // 获取index节点的前一个节点
            Node beforeNode = getIndexNode(index - 1);

            // 获取index节点的后一个节点
            Node afterNode = beforeNode.next.next;

            // index下标的节点
            Node node = beforeNode.next;
            node.next = null;

            beforeNode.next = afterNode;
        }
        size--;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

至于查询和修改操作不涉及到指针变化，但由于链表的存储特点，所以查询和修改都需要遍历链表才能完成，所以查询和修改的时间复杂度为O(n)，而插入和删除的时间复杂度为O(1)，这正好和数组的特征相反。

综上数组的优点是快速定位所以读多写少的场景会很适合，而链表的优势在于插入和删除更加灵活。