VSC/SMC(十六)——自适应鲁棒滑模控制

目录

1.参数不定和扰动不定但有界的系统

 2.滑模控制自适应律设计

2.1控制律设计总结

3.仿真分析

3.1 PD控制

3.2普通自适应律

3.3映射自适应律

3.4总结

4学习问题

---

1.参数不定和扰动不定但有界的系统

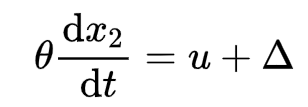
其中： 

 

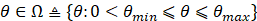
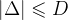
 2.滑模控制自适应律设计

设计滑模面：

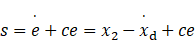
由于θ有界不定，所以用θ^代替θ 

 

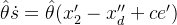
稳定性证明：

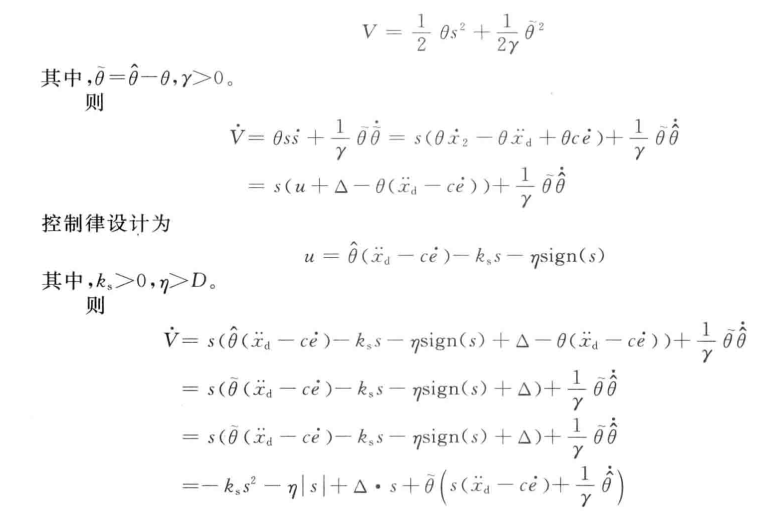
2.1控制律设计总结

其设计的思想还是可以用等效滑模项+鲁棒滑模项进行解释：

①定义滑模面：s = e'+c*e，则:s' = e''+c*e' = (u+Δ)/θ-xd''+c*e'，不考虑扰动Δ，令s' = 0，所以得到等效项ueq = θ*(xd''-c*e')；

②选取指数趋近律：s' = -k*s-η*sign(s)，所以鲁棒项usw = θ*(-k*s-η*sign(s))，所以滑模控制律为：u = ueq+usw = θ*(xd''-c*e'-k*s-η*sign(s))，注η > |Δ|。

③将θ换成θ^，即θ的估计值，也是自适应律，定义自适应律为θ^ = -γ*s*(xd''-c*e')；选取Lyapunov函数进行闭环系统稳定性证明(见上图片)。

④这里为了防止自适应律过大而导致输入信号过大等问题，引入映射自适应算法对自适应律进行修正(见上图片)。

3.仿真分析

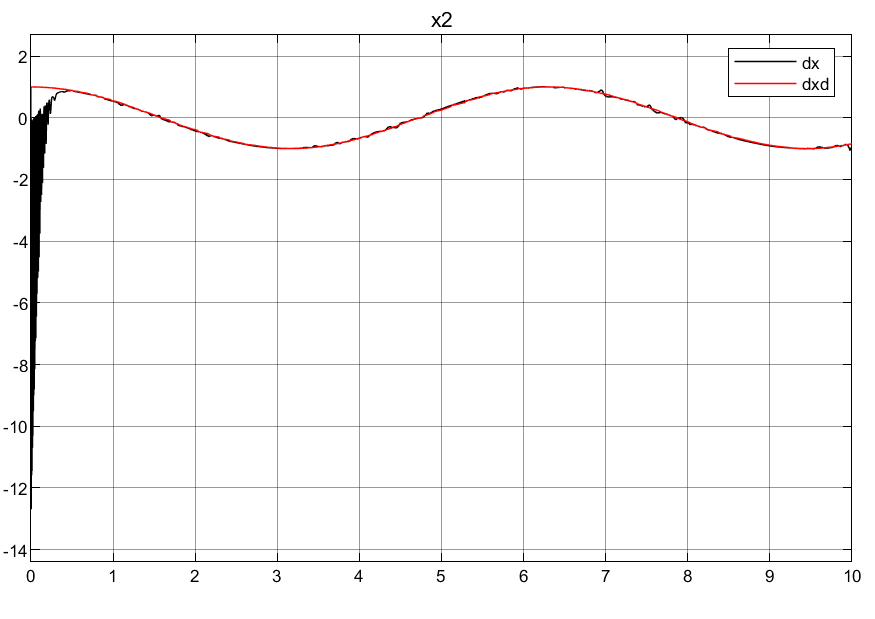
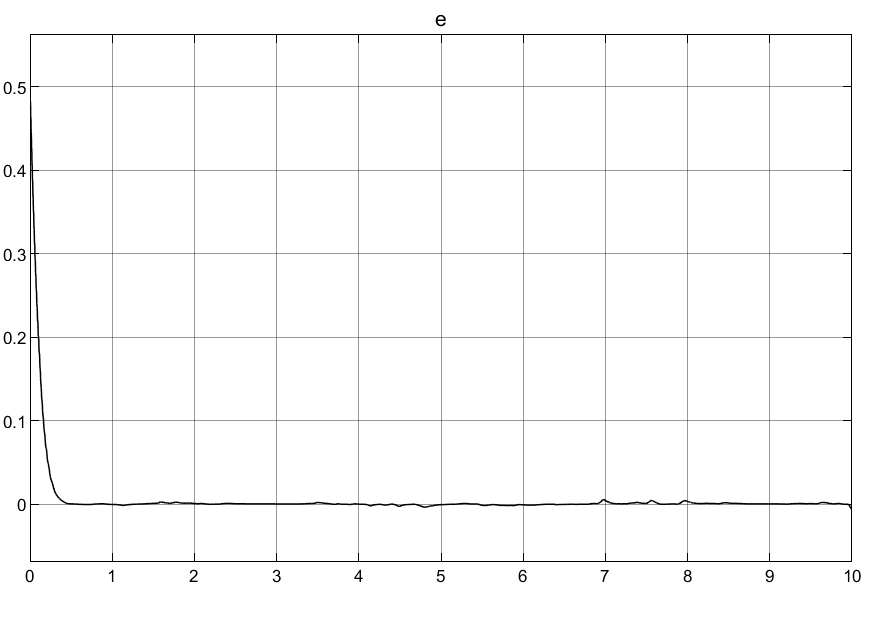
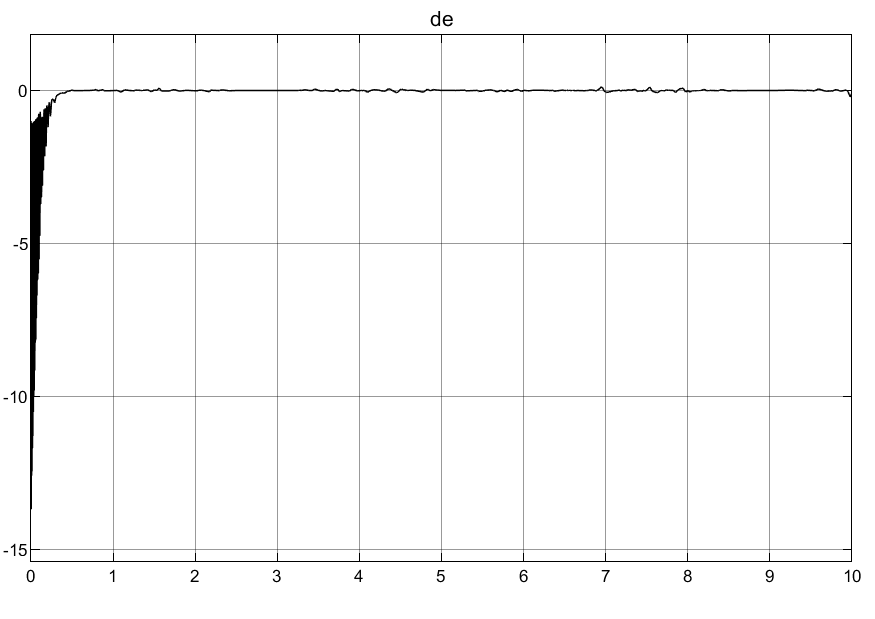
取θ = 1，系统不确定性波动θmin = 0.5 <= θ <= θmax = 1.5，不确定扰动Δ=0.5*x2+1.5*sign(x2)，所以扰动边界D = 2；初始状态定位[0.5;0]。

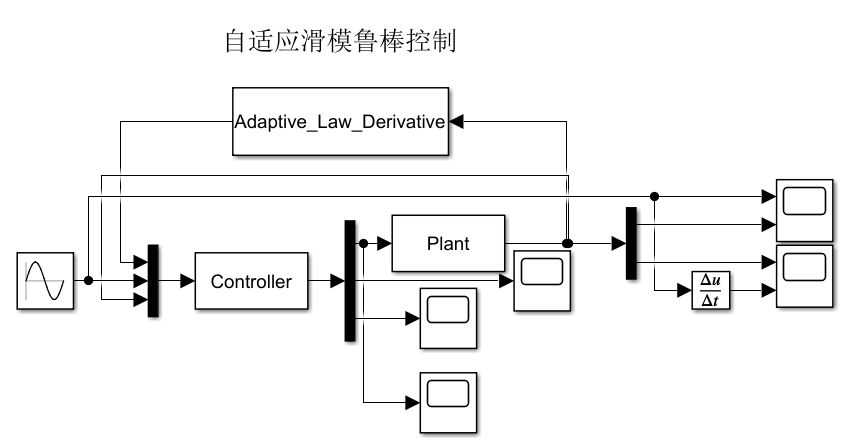
3.1 PD控制

这里我是采用的s函数编写pd控制器，这个很简单，但是调参需要人为调节，我前面的文章介绍了PID Tune，推荐使用这个，文章在这里：

基于抗积分饱和(Anti-windup)的自适应PID控制(白嫖程序模型)_Mr. 邹的博客-CSDN博客

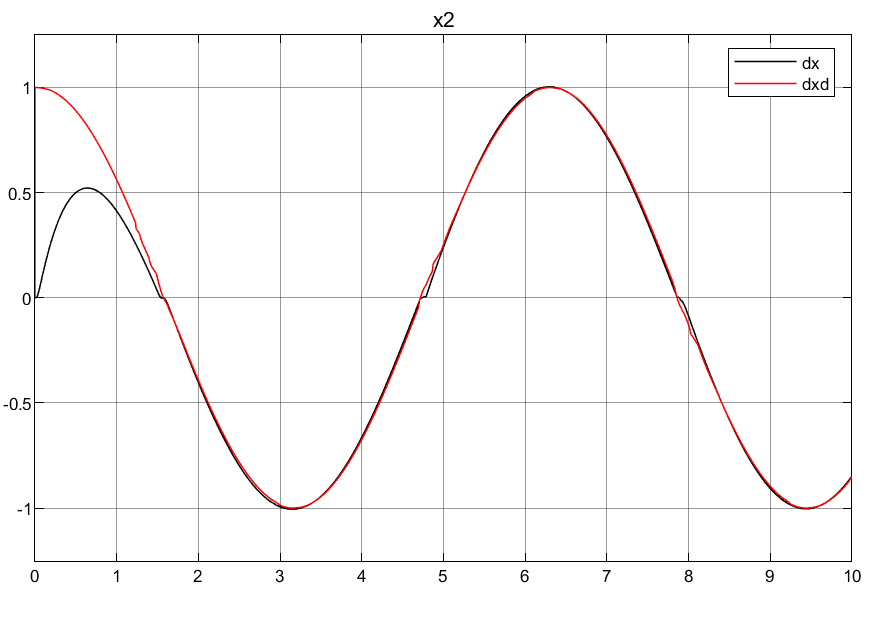
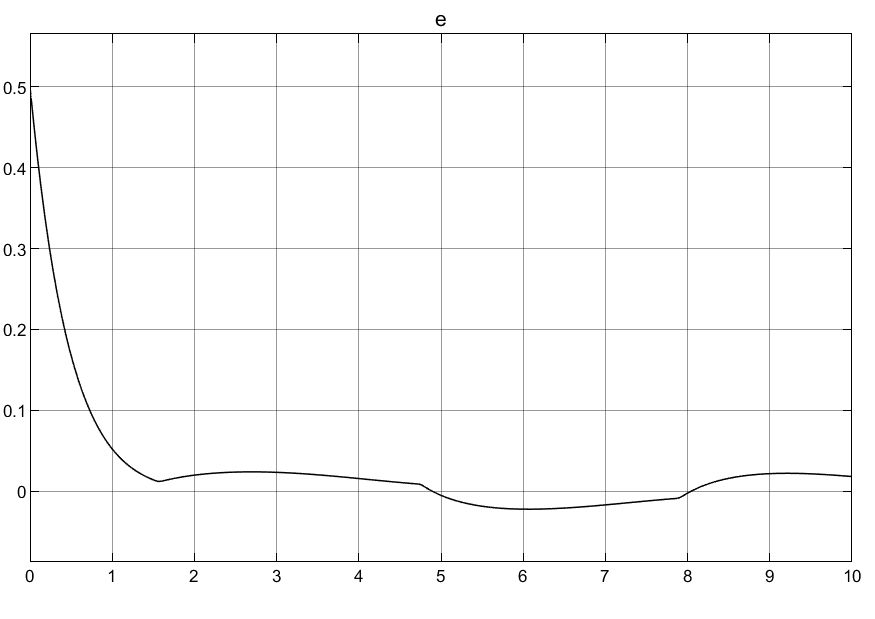
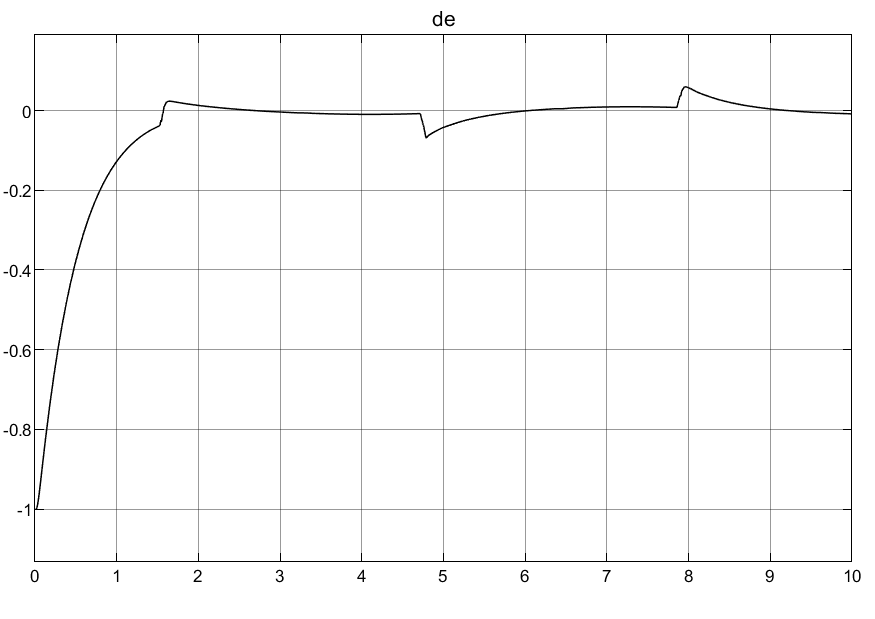
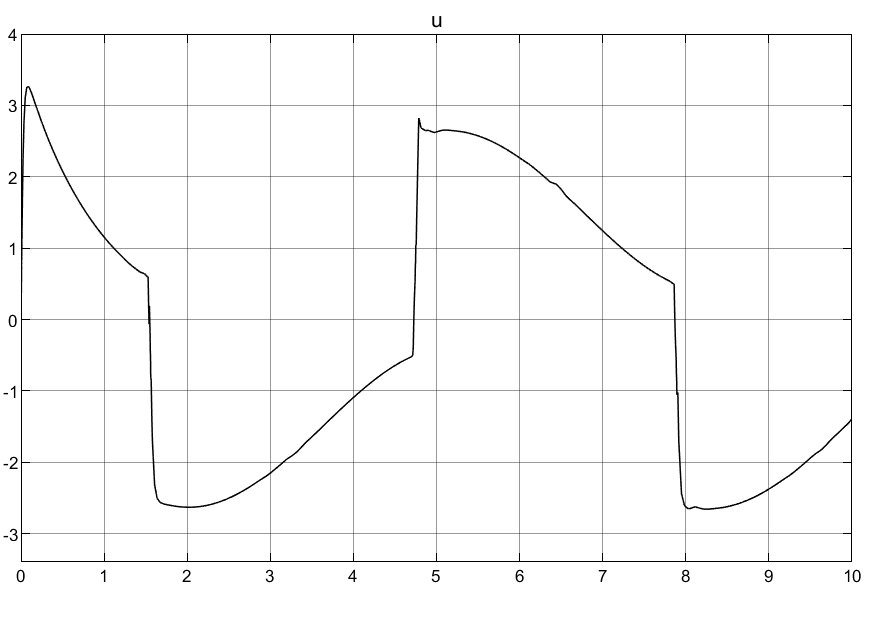
3.2普通自适应律

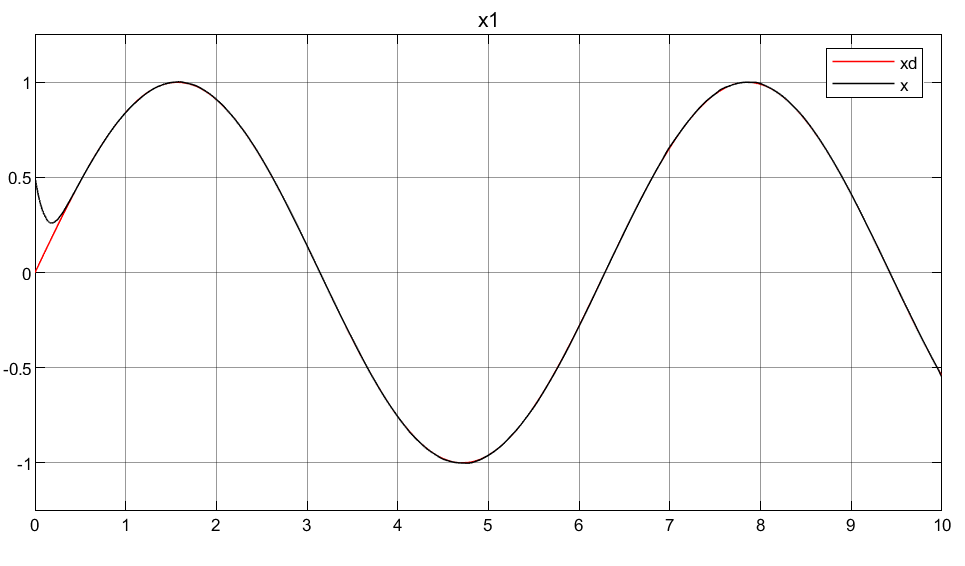
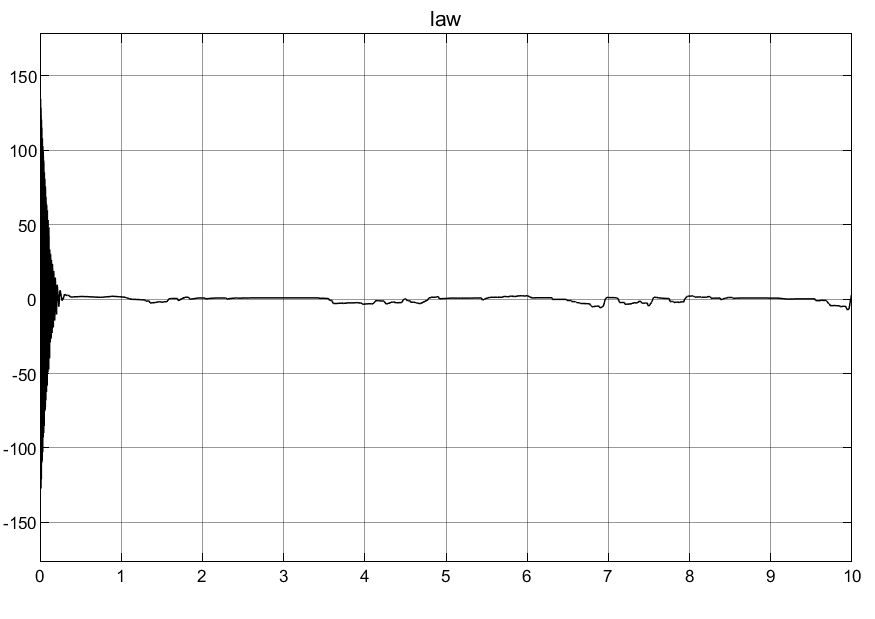
3.3映射自适应律

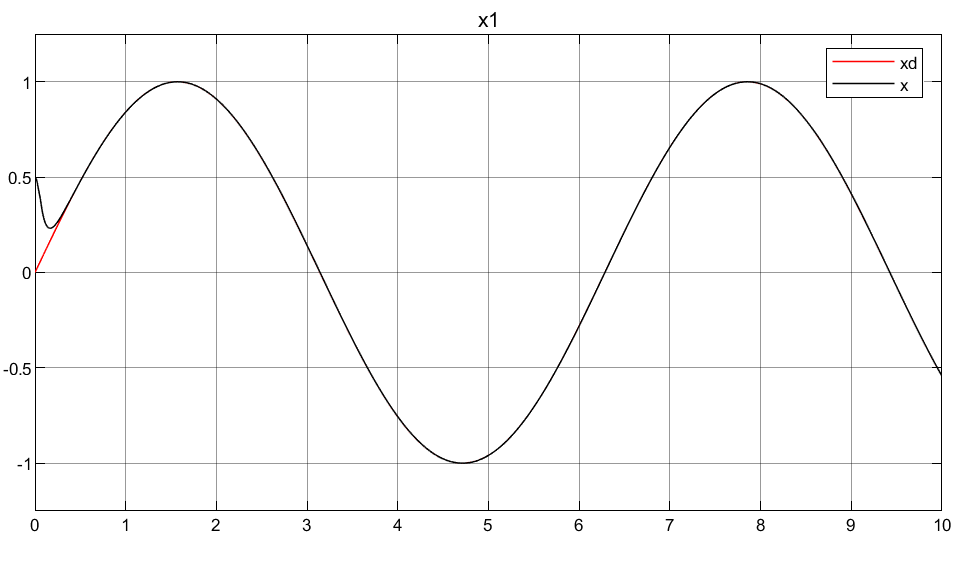
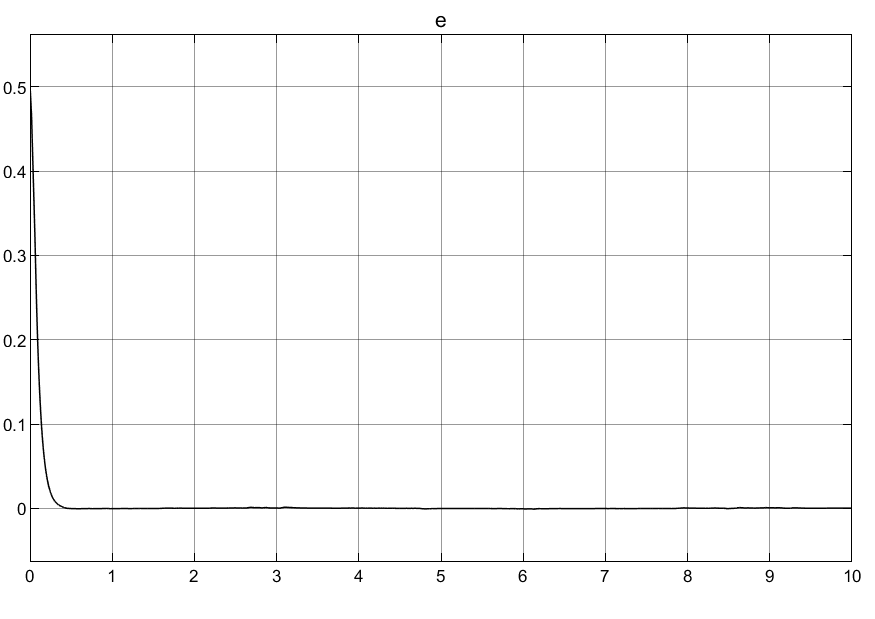
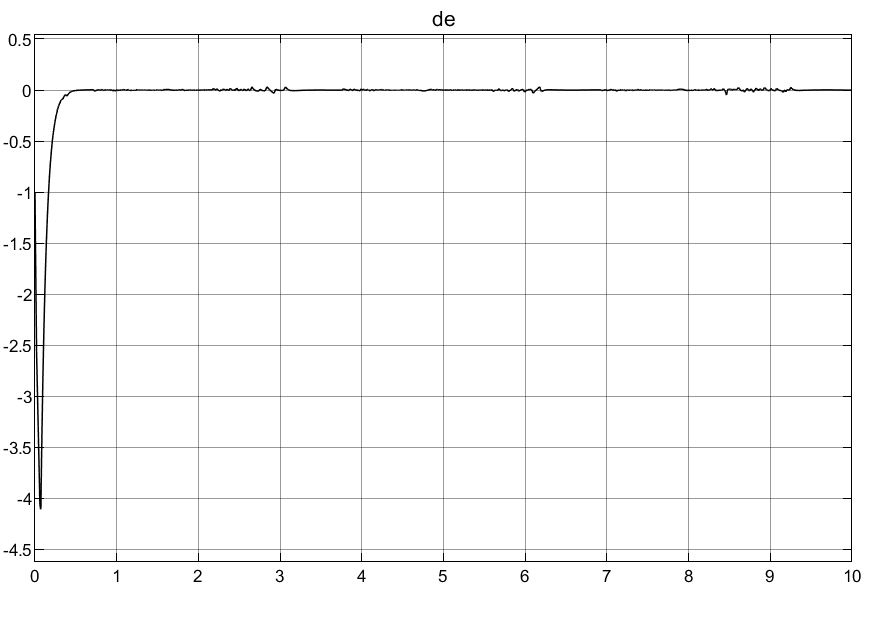
3.4总结

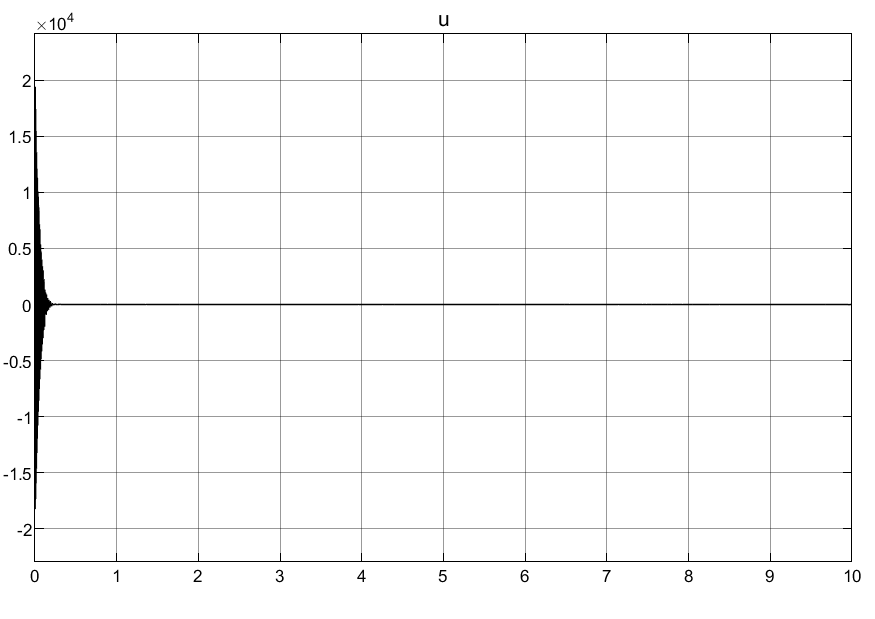
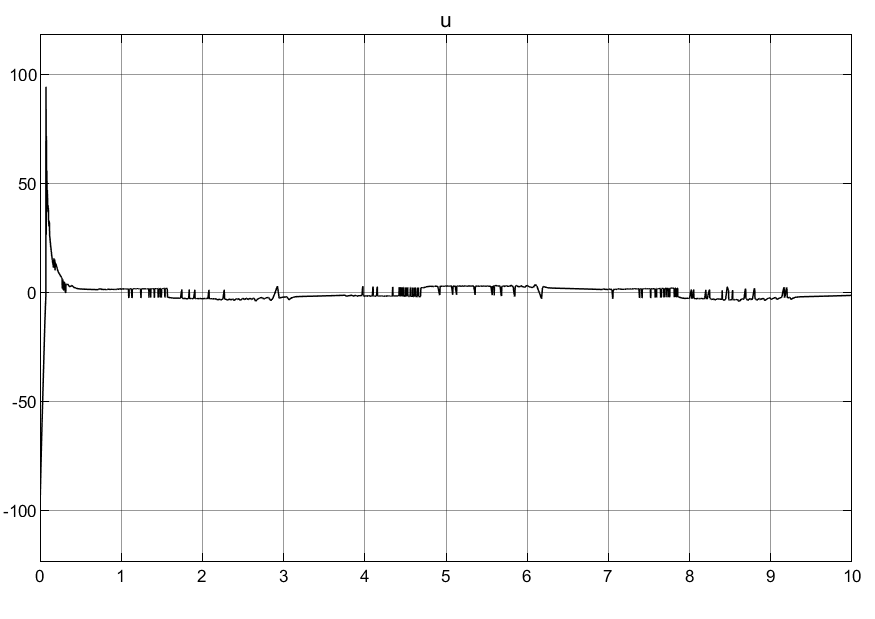
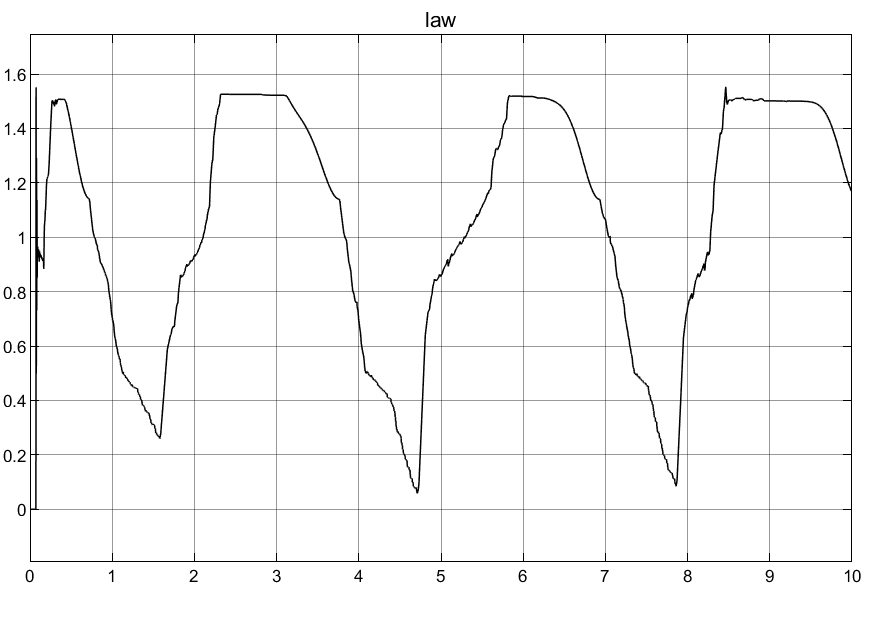
①可以看到普通自适应律刚开始的控制输入超调量过大，导致刚开始的时候产生较大的抖动。

②本例中个人对自适应律的理解：因为系统θ的不确定性，所以需要针对其提出估计θ^，也就是自适应律，但是普通的自适应律没有范围限定，也就是没有系统不确定性边界调节，会导致控制输入过大情况，所以需要加上边界条件对自适应律进行限制，也就是后面的映射自适应律。

③可以看到映射自适应律使得初始控制输入的过冲很小，这对于底层执行器的响应是非常友好的，对于实际意义很大！

4学习问题

进行调试的时候一定要先进行求解器的设置，尽量不要取使用系统自动选择的求解器，本实例仿真中我就是用默认求解器去调试结果发了控制器和控制律编写没问题，但是仿真结果确实错的，找了好久问题，踩了这个坑，才知道求解器不仅仅影响求解速度还会导致结果错误！

建议：如果使用变步长，推荐使用ode45求解器；如果定步长，推荐ode4求解器，步长为0.001s。

如果有帮助，麻烦帮忙点个赞是我最大的分享动力，非常感谢！

注：仅为便利自己学习，错误在所难免，如有侵权，请联系删除，有兴趣的学者可以参考学习交流，谢谢！