《算法导论》18.2 B树上的基本操作（搜索、创建、插入）（包含C++代码）

一、约定

本节将给出B-TREE-SEARCH、B-TREE-CREATE和B TREE-INSERT操作的细节。在这些过程中，我们采用两个约定:
●B树的根结点始终在主存中，这样无需对根做DISK-READ操作;然而，当根结点被改变后，需要对根结点做一次DISK-WRITE操作。
●任何被当做参数的结点在被传递之前，都要对它们先做一次DISK-READ操作。
给出的过程都是“单程”算法，即它们从树的根开始向下，没有任何返回向上的过程。

二、搜索B树

1、对每个内部结点x，做的是(x.n+1)路的分支选择。
2、B-TREE-SEARCH是定义在二叉搜索树上的TREE-SEARCH过程的一个直接推广。它的输入是一个指向某子树根结点x的指针，以及要在该子树中搜索的一个关键字k。因此，顶层调用的形式为B-TREE-SEARCH(T. root, k)。如果k在B树中，那么B-TREE-SEARCH返回的是由结点y和使得y. key_i=k的下标i组成的有序对(y, i)；否则，过程返回NIL。

B-TREE-SEARCH
i = 1
while i <= x.n and k > x.keyi
	i = i+1
if i <= x.n and k == x.keyi	//i小于x存储的关键字个数且等于其中一个值
	return(x,i)
elseif x.leaf	//如果x是叶结点，直接返回
	return NIL
else DISK-READ(x,ci)//如果x不是叶结点，继续调用函数
	return B-TREE-SEARCH(x,ci,k)
1
2
3
4
5
6
7
8
9
10

三、创建一棵B树

为构造一棵B树T，先用B-TREE-CREATE来创建一个空的根结点，然后调用B-TREE-INSERT来添加新的关键字。这些过程都要用到一个辅助过程ALLOCATE-NODE，它在O(1)时间内为一个新结点分配一个磁盘页。我们可以假定由ALLOCATE-NODE所创建的结点并不需要DISK-READ,因为磁盘上还没有关于该结点的有用信息。

B-TREE-CREATE(T)
x = ALLOCATE-NODE()
x.leaf = TRUE
x.n = 0
DISK-WRITE(x)
T.root = x
1
2
3
4
5
6

四、向B树中插入一个关键字

1、将新的关键字插入一个已经存在的叶结点上。由于不能将关键字插入一个满的叶结点，故引入一个操作，将一个满的结点y(有2t-1个关键字)按其中间关键字( median key)y. key~t，分裂(split)为两个各含t-1个关键字的点。
2、中间关键字被提升到y的父结点，以标识两棵新树的划分点。但是如果y的父结点也是满的，就必须在插入新的关键字之前将其分裂，最终满结点的分裂会沿着树向上传播。
3、与一棵二叉搜索树一样，可以在从树根到叶子这个单程向下过程中将一个新的关键字插入B树中。为了做到这一点，当沿着树往下查找新的关键字所属位置时，就分裂沿途遇到的每个满结点(包括叶结点本身)。因此就能确保每当要分裂一个满结点y时，它的父结点不是满的。

分裂B树中的结点

过程B-TREE-SPLIT-CHILD的输入是一个非满的内部结点x(假定在主存中)和一个使x.c_i(也假定在主存中)为x的满子结点的下标i。
该过程把这个子结点分裂成两个，并调整x，使之包含多出来的孩子。要分裂一个满的根，首先要让根成为一个新的空根结点的孩子，这样才能使用B-TREE-SPLIT-CHILD。树的高度因此增加；分裂是树长高的唯一途径。

B-TREE-SPLIT-CHILD(x,i)
z = ALLOCATE-NODE()
y = x.ci			//x是被分裂的结点，y是x的第i个孩子
z.leaf = y.leaf	
z.n = t - 1
//将y的t-1个关键字给z
for j = 1 to t-1
	z.keyj = y.key(j+t)
if not y.leaf
	for j = 1 to t
		z.cj = y.c(j+t)	
y.n = t - 1	//调整y关键字个数
//将z插入为x的一个孩子
for j = x.n + 1 downto i + 1	//从i+1个孩子开始x的所有孩子都往后移动一位
	x.c(j+1) = x.cj
x.ci+1 = z						//x的第i+1个孩子成为z
for j = x.n downto i			//x的关键字也和前面一样
	x.key(j+1) = x.keyj
//提升y的中间关键字到x来分隔y和z
x.keyi = y.keyt
x.n = x.n + 1
//写出所有修改过的磁盘界面
DISK-WRITE(y)
DISK-WRITE(z)
DISK-WRITE(x)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

以沿树单程下行方式向B树插入关键字

B-TREE-INSERT(T,k)
r = T.root
if r.n == 2t-1		//处理根结点为满的情况
	s = ALLOCATE-NODE()
	T.root = s
	s.leaf = FALSE
	s.n = 0
	s.c1 = r
	B-TREE-SPLIT-CHILD(s,1)
	B-TREE-INSERT-NONFULL(s,k)
else
	B-TREE-INSERT-NONFULL(r,k)
1
2
3
4
5
6
7
8
9
10
11
12

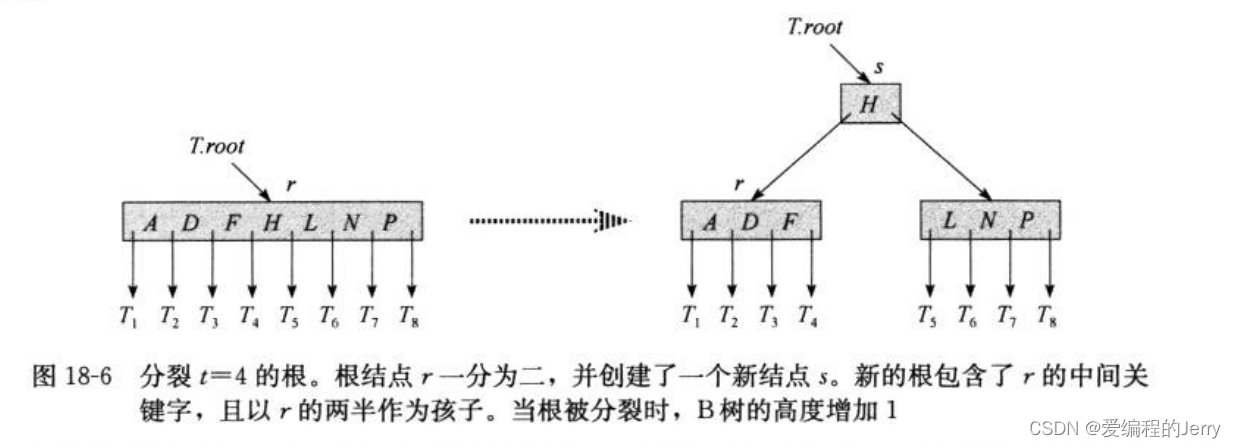
辅助的递归过程B-TREE-INSERT-NONFULL将关键字插入结点x，要求假定在调用该过程时x是非满的。操作B-TREE-INSERT和递归操作B-TREE-INSERT-NONFULL保证了这个假设成立。

B-TREE-INSERT-NONFULL(x,k)
i = x.n
if x.leaf
	//从尾部开始遍历，当k小于keyi的时候，不断将keyi向后移动一位，直到找到
	while i >= 1 and k < x.keyi
		x.key(i+1) = x.keyi
		i = i-1
	x.key(i+1) = k	//赋值
	x.n = x.n + 1
	DISK-WRITE(x)
else while i >= 1 and k < x.key	//决定向x的哪个子结点递归下降
		i = i - 1
	i = i + 1
	DISK-READ(x,ci)
	if x.ci.n == 2t - 1		//检查是否递归降至了一个满子结点上
		B-TREE-SPLIT-CHILD(x,i)
		if k > x.keyi	//确认向两个孩子中哪一个下降是对的
			i = i + 1
	B-TREE-INSERT-NONFULL(x,ci,k) //递归地将k插入到合适的子树中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

四、C++代码

#include 
using namespace std;
static const int m = 3;  //定义最小度为3
static const int key_max = 2 * m - 1;//关键字最大个数
static const int key_min = m - 1;//关键字最小个数
static const int child_max = key_max + 1;//子节点最大个数(这里可以看出子节点数与关键字数有关)
static const int child_min = key_min + 1;//子节点最小个数

template <class T>
class BTree;//前置声明

template <class T>
class BTnode
{
    friend class BTree<T>;//友元函数
public:
    BTnode()
    {
        keyNum = 0;
        parent = NULL;//父节点初始化
        isleaf = true;
        int i;
        for (i = 0; i < child_max; i++)//子树指针数组初始化
        {
            pchild[i] = NULL;
        }
        for (i = 0; i < key_max; i++)//关键字数组初始化
        {
            keyvalue[i] = '\0';
        }
    }
private:
    bool isleaf;//判断节点是否是叶子节点
    int keyNum;//关键字个数
    BTnode<T>* parent;//指向父节点
    BTnode<T>* pchild[child_max];//子树指针数组
    T   keyvalue[key_max];//关键字数组
};

template <class T>
class BTree
{
public:
    //构造函数
    BTree()
    {
        root = NULL;
    }

   //函数作用:插入关键字
    bool BTree_insert(T value)
    {
        if (contain(value))//看树中是否有相同的关键字
        {
            return false;
        }
        else
        {
            if (root == NULL)
            {
                root = new BTnode<T>();
            }
            if (root->keyNum == key_max)
            {
                BTnode<T>* newnode = new BTnode<T>();
                newnode->pchild[0] = root;
                newnode->isleaf = false;//由上步操作可知newnode已经有子节点
                SplitBlock(newnode, 0, root);//分块操作
                root = newnode;//更新根节点
            }
            Notfull_insert(root, value);//插入块未满的操作
            return true;
        }
    }

    //分裂结点
    void SplitBlock(BTnode<T>* node_parent, int child_index, BTnode<T>* node_child)
    {
        BTnode<T>* node_right = new BTnode<T>();
        node_right->isleaf = node_child->isleaf;
        node_right->keyNum = key_min;
        int i;
        //node_right拷贝关键字
        for (i = 0; i < key_min; i++)
        {
            node_right->keyvalue[i] = node_child->keyvalue[i + child_min];
        }
        //判断分裂的节点是否是叶子节点,如果不是的话就要把它的孩子赋值过去
        if (!node_child->isleaf)
        {
            for (i = 0; i < child_min; i++)
            {
                node_right->pchild[i] = node_child->pchild[i + child_min];
                node_child->pchild[i + child_min]->parent = node_right->pchild[i];
            }
        }
        node_child->keyNum = key_min;//更新子节点的关键字数
        //把父节点关键字和子指针往后移 倒序赋值
        for (i = node_parent->keyNum; i > child_index; i--)
        {
            node_parent->keyvalue[i] = node_parent->keyvalue[i - 1];
            node_parent->pchild[i + 1] = node_parent->pchild[i];
            node_child->pchild[i]->parent = node_parent->pchild[i + 1];
        }
        node_parent->keyNum++;//更新父节点关键字数
        node_parent->pchild[child_index + 1] = node_right;
        node_right->parent = node_parent->pchild[child_index + 1];
        //把中间的那个关键字上移到父节点
        node_parent->keyvalue[child_index] = node_child->keyvalue[key_min];
    }

    //函数作用:往没有满的节点中增加关键字
    void Notfull_insert(BTnode<T>* node, T value)
    {

        int node_keynum = node->keyNum;//获取节点关键字数
        if (node->isleaf)//node是叶子节点
        {
            while (node_keynum > 0 && value < node->keyvalue[node_keynum - 1])
            {
                node->keyvalue[node_keynum] = node->keyvalue[node_keynum - 1];//把关键字往后移动
                --node_keynum;
            }
            node->keyvalue[node_keynum] = value;
            node->keyNum++;
        }
        else//node是内部节点
        {
            while (node_keynum > 0 && value < node->keyvalue[node_keynum - 1])
            {
                --node_keynum;
            }
            //在比它小和比它大中间那个子节点中找合适位置,
            //如果它比所有的都小则在第一个子节点中寻找
            BTnode<T>* node_child = node->pchild[node_keynum];
            if (node_child->keyNum == key_max)
            {
                SplitBlock(node, node_keynum, node_child);
                if (value > node->keyvalue[node_keynum])//插入值和子节点中间的值比较
                {
                    node_child = node->pchild[node_keynum + 1];
                }
            }
            Notfull_insert(node_child, value);//继续往下寻找合适的位置
        }
    }

    //查找是否有相同元素在数中
    bool contain(T value)
    {
        if (BTree_find(root, value) != NULL)
            return true;
        return false;
    }

    //函数作用:查找是否有相同元素在树中
    BTnode<T>* BTree_find(BTnode<T>* node, T value)
    {
        if (node == NULL)//当前节点为空的时候
        {
            return NULL;
        }
        else//当前节点不为空
        {
            int i;
            //在比它小和比它大的中间子节点中寻找相等的
            for (i = 0; i < node->keyNum; i++)
            {
                if (value <= node->keyvalue[i])
                {
                    break;
                }
            }
            //校验当前的关键字是否等于查找的关键字
            if (i < node->keyNum && value == node->keyvalue[i])//i是下标最大值keyNum-1
            {
                return node;
            }
            else
            {
                //如果之前比查找关键没有相等的关键字并且当前节点是叶子节点的话
                //那么在B树中没有一样的关键字(因为后面比关键字更大)
                if (node->isleaf)
                {
                    return NULL;
                }
                else//如果不是叶子节点则在下面的子节点中寻找
                {
                    return BTree_find(node->pchild[i], value);//这里的return别忘了
                }
            }
        }
    }

    //打印元素
    void printpoint(BTnode<T>* node, int count)
    {
        if (node != NULL)//判断元素是否为空
        {
            int i, j;
            //每个节点从小到大打印
            for (i = 0; i < node->keyNum; i++)
            {
                //判断是否叶节点,不是的话则要往子节点中寻找打印
                if (!node->isleaf)//判断是否是叶子节点
                {
                    printpoint(node->pchild[i], count - 3);
                }
                for (j = count; j >= 0; j--)
                {
                    cout << "-";
                }
                cout << "|" << node->keyvalue[i] << "|" << endl;
            }
            if (!node->isleaf)//子节点数比关键字数多一个
            {
                printpoint(node->pchild[i], count - 3);
            }
        }
    }

    //printpoint无参函数传递值过去
    void printpoint()
    {
        printpoint(root, key_max * 5);
    }
private:
    BTnode<T>* root;//根节点
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229