无人机中的坐标系与相机姿态计算

球坐标系

球坐标系是三维坐标系中的一种，在无人机中一般使用球坐标系来表示相机姿态，相机姿态的坐标是相对于无人机的，而无人机的飞行姿态则是相对于大地坐标系的。这里我们使用的相机是2自由度的相机，即可以水平 $\varphi$ 和垂直 $\theta$ 两个方向转动，其中 $\varphi \in [0,2\pi ]$ 或 $[-\pi ,\pi ]$，$\theta \in [0,\pi ]$，这里 $\rho$ 为球半径（默认我们使用右手坐标系）

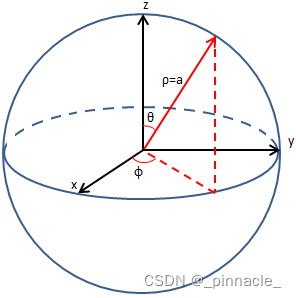
球坐标与笛卡尔坐标的转换

在后面的计算中因为球坐标不方便作旋转变换，我们需要用到球坐标与笛卡尔坐标的坐标转换

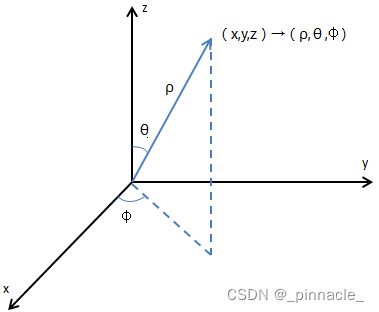
球坐标到笛卡尔坐标

  $x=\rho \ast sin(\theta )\ast cos(\varphi )$

  $y=\rho \ast sin(\theta )\ast sin(\varphi )$

  $z=\rho \ast cos(\theta )$

笛卡尔坐标到球坐标

  $\rho =\sqrt{x^2+y^2+z^2}$

  $\theta =arccos(z÷\rho )$

  $\varphi =arctan(y,x)$

相机相对大地坐标系的姿态

为了计算方便，我们一般旋转坐标系将$z$轴向下，这个时候无人机机头方向即是 $x$ 轴方向，$\varphi$即是相对于无人机机头的相机水平旋转角度，$\theta$在垂直于无人机方向上为0度；这时的无人机载体的坐标系就是我们常用的北东地坐标系（NED，即$x$轴指向北，$y$轴指向东，$z$轴指向地面）。

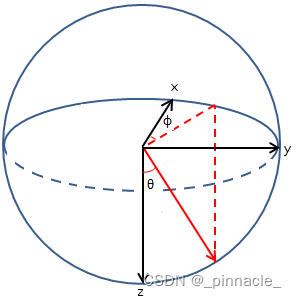
在无人机飞行中，无人机平台由于飞行运动及气流运动等因素，会影响无人机的飞行姿态，这时搭载的相机姿态相对大地坐标系会发生变化，需要加入无人机姿态去计算修正，以便于更准确计算相机的观测位置

无人机姿态一般包括3个角度即：偏航角(Yaw)、俯仰角(Pitch)、翻滚角(Roll)。偏行角一般指无人机相对北极的顺时针角度，也即整个坐标系沿 $z$ 轴顺时针旋转的角度，俯仰角即飞机的攻角或者飞机机头的俯仰角，在上面的坐标系中是沿 $y$ 轴旋转的角度。翻滚角则是飞机左右倾斜的角度，在上面的坐标系中是沿 $x$ 轴旋转的角度。

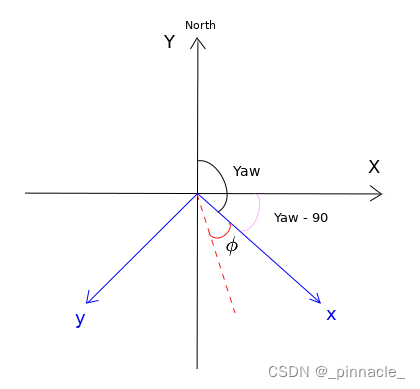
以上需要注意的是：偏航角与其他角不同，这里偏航角的旋转的角度是：$Yaw-90$，如上图，是3维坐标系的俯视图，蓝色坐标系即是无人机载体坐标系NED，黑色坐标系即是大地坐标系。所以这里无人机载体的坐标系是相对于大地坐标系顺时针旋转了$Yaw-90$度。另一个需要注意的是：最后得到的相机水平 $\varphi$ 角度需要取反，即 $-\varphi$;因为NED坐标系和大地坐标系中$y$轴是对称的，如：上图可将蓝色$x$轴转到$X$轴上，这时俩坐标系$y$轴是对称的，所以角度是相反的。

三维空间的旋转矩阵

沿 $x$ 轴的旋转

   R x ( α ) = [ 1 0 0 0 c o s ( α ) − s i n ( α ) 0 s i n ( α ) c o s ( α ) ] R_x(\alpha)=

Rx​(α)= ​100​0cos(α)sin(α)​0−sin(α)cos(α)​ ​

沿 $y$ 轴的旋转

   R y ( β ) = [ c o s ( β ) 0 s i n ( β ) 0 1 0 − s i n ( β ) 0 c o s ( β ) ] R_y(\beta)=

Ry​(β)= ​cos(β)0−sin(β)​010​sin(β)0cos(β)​ ​

沿 $z$ 轴的旋转

   R z ( γ ) = [ c o s ( γ ) − s i n ( γ ) 0 s i n ( γ ) c o s ( γ ) 0 0 0 1 ] R_z(\gamma)=

Rz​(γ)= ​cos(γ)sin(γ)0​−sin(γ)cos(γ)0​001​ ​

合并旋转后的三维旋转矩阵

  $R_{3d}=R_z(\gamma )R_y(\beta )R_x(\alpha )$

这里需要注意的是：1.旋转矩阵相乘的顺序，矩阵乘法不满足交换律，所以不同顺序一般最后得到的相机旋转角度不同（比较常用的顺序为 $XYZ$ 和 $ZYX$，这个依赖于惯性测量单元(IMU)的姿态解算约定的旋转顺序 ）。 2. 旋转方向，这里默认写的都是正向旋转。下面贴一下逆向的旋转矩阵作为参考：

沿 $x$ 轴的逆向旋转

   R x c ( α ) = [ 1 0 0 0 c o s ( α ) s i n ( α ) 0 − s i n ( α ) c o s ( α ) ] R_x^c(\alpha)=

Rxc​(α)= ​100​0cos(α)−sin(α)​0sin(α)cos(α)​ ​

沿 $y$ 轴的逆向旋转

   R y c ( β ) = [ c o s ( β ) 0 − s i n ( β ) 0 1 0 s i n ( β ) 0 c o s ( β ) ] R_y^c(\beta)=

Ryc​(β)= ​cos(β)0sin(β)​010​−sin(β)0cos(β)​ ​

沿 $z$ 轴的逆向旋转

   R z c ( γ ) = [ c o s ( γ ) s i n ( γ ) 0 − s i n ( γ ) c o s ( γ ) 0 0 0 1 ] R_z^c(\gamma)=

Rzc​(γ)= ​cos(γ)−sin(γ)0​sin(γ)cos(γ)0​001​ ​

很显然 $R_x^c(\alpha )=R_x(-\alpha )$，同理沿其他轴也是一样的，所以两种矩阵是形式等价的，只用一种就行了，注意旋转方向的正负。

代码实现

from math import *
import numpy as np

def rad(x):
    return radians(x)

def deg(x):
    return degrees(x)

def coord_sphere2cart(theta,phi, rho = 1):
    x = rho*sin(rad(theta))*cos(rad(phi))
    y = rho*sin(rad(theta))*sin(rad(phi))
    z = rho*cos(rad(theta))
    return x,y,z

def coord_cart2sphere(x,y,z):
    rho = sqrt(x**2+y**2+z**2)
    theta = acos(z/rho)
    phi = atan2(y,x)
    return rho,deg(theta),deg(phi)

def uav_rot(x,y,z,RX,RY,RZ):
    R = rad(RX) #Roll-X
    P = rad(RY) #Pitch-Y
    Y = rad(RZ) #Yaw-Z
    
    Rx = [[1,0,0],
          [0,cos(R),-sin(R)],
          [0,sin(R),cos(R)]]
    Ry = [[cos(P),0,sin(P)],
          [0,1,0],
          [-sin(P),0,cos(P)]]
    Rz = [[cos(Y),-sin(Y),0],
          [sin(Y),cos(Y),0],
          [0,0,1]]
    Rx = np.array(Rx)
    Ry = np.array(Ry)
    Rz = np.array(Rz)
    R3d = Rz @ Ry @ Rx
    xyz = np.array([x,y,z])
    return R3d @ xyz

def camera_rectify(pan,tilt,yaw,pitch,roll):
    x,y,z = coord_sphere2cart(theta=tilt,phi=pan,rho=1)
    x_,y_,z_ = uav_rot(x,y,z,RX=roll,RY=pitch,RZ=yaw)
    rho,theta,phi = coord_cart2sphere(x_,y_,z_)
    pan = phi
    tilt = theta
    return pan,tilt
    
def rot_mat_to_symbol():
    from sympy import Symbol,Matrix,sin,cos
    R = Symbol("R") #Roll-X
    P = Symbol("P")  #Pitch-Y
    Y = Symbol("Y") #Yaw-Z
    
    x = Symbol("x")
    y = Symbol("y")
    z = Symbol("z")
    xyz = Matrix([[x],[y],[z]])

    Rx = Matrix([[1,0,0],
                 [0,cos(R),-sin(R)],
                 [0,sin(R),cos(R)]
                ])

    Ry = Matrix([[cos(P),0,sin(P)],
                 [0,1,0],
                 [-sin(P),0,cos(P)],
                ])

    Rz = Matrix([[cos(Y),-sin(Y),0],
                 [sin(Y),cos(Y),0],
                 [0,0,1]
                ])

    res = Rz*Ry*Rx*xyz
    for a,m in zip(xyz,res):
        print(a,"=",m)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

参考：

1. Geometric transformations in 3D and coordinate frames