-
偏差与方差
error due to “bias” and error due to “variance”
假设 y ^ \hat{y} y^ 是最正确的函数
-
From training data,我们可以找到 f ∗ f^* f∗
-
f ∗ i s a n e s t i m a t o r o f f ^ f^*\,\,\,is\,\,\,an\,\,\,estimator\,\,\,of\,\,\,\hat{f} f∗isanestimatoroff^
那么 f ∗ f^* f∗ 与 f ^ \hat{f} f^ 的距离,可能是由偏置项bias和variance组成的
——偏差和方差
Bias and Variance of Estimator
-
Estimate the mean of a variable x
估计x的均值
-
assume the mean of x is μ \mu μ
-
assume the variance of x is σ 2 \sigma^2 σ2
-
Estimator of mean μ \mu μ ——估计 μ \mu μ 值
-
Sample N points: { x 1 , x 2 , . . . , x N } \{x^1,x^2,...,x^N\} {x1,x2,...,xN}
采样N个点
-
m = 1 N ∑ N x N m=\frac{1}{N}\sum_{N}x^{N} m=N1N∑xN
-
m = 1 N ∑ N x N ≠ μ m=\frac{1}{N}\sum_{N}x^{N}\neq \mu m=N1∑NxN=μ
但是我们如果对m取期望值
E [ m ] = E [ 1 N ∑ N x N ] = 1 N ∑ N E [ x N ] = μ E[m]=E[\frac{1}{N}\sum_{N}x^{N}]=\frac{1}{N}\sum_NE[x^N]=\mu E[m]=E[N1N∑xN]=N1N∑E[xN]=μ这个m的偏差能偏差多少,取决于
V a r i a n c e [ m ] = σ 2 N Variance[m]=\frac{\sigma^2}{N} Variance[m]=Nσ2
m的方差取决于这个采样的数目,N越大的时候,方差值越小Estimator of varicance σ 2 \sigma^2 σ2
- Sample N points: { x 1 , x 2 , . . . , x N } \{x^1,x^2,...,x^N\} {x1,x2,...,xN}
m = 1 N ∑ N x N s 2 = 1 N ∑ N ( x N − m ) 2 m=\frac{1}{N}\sum_Nx^N\\ s^2=\frac{1}{N}\sum_N(x^N-m)^2 m=N1N∑xNs2=N1N∑(xN−m)2
- Biased estimator
E [ s 2 ] = N − 1 N σ 2 E[s^2]=\frac{N-1}{N}\sigma^2 E[s2]=NN−1σ2
这里取期望值,并不是直接等于 σ 2 \sigma^2 σ2
——Bias反映的是,你瞄准的靶心是不是正确的
——Variance反映的是,你的技术会导致你离你瞄准的位置有多远

f ∗ f^* f∗重复实验
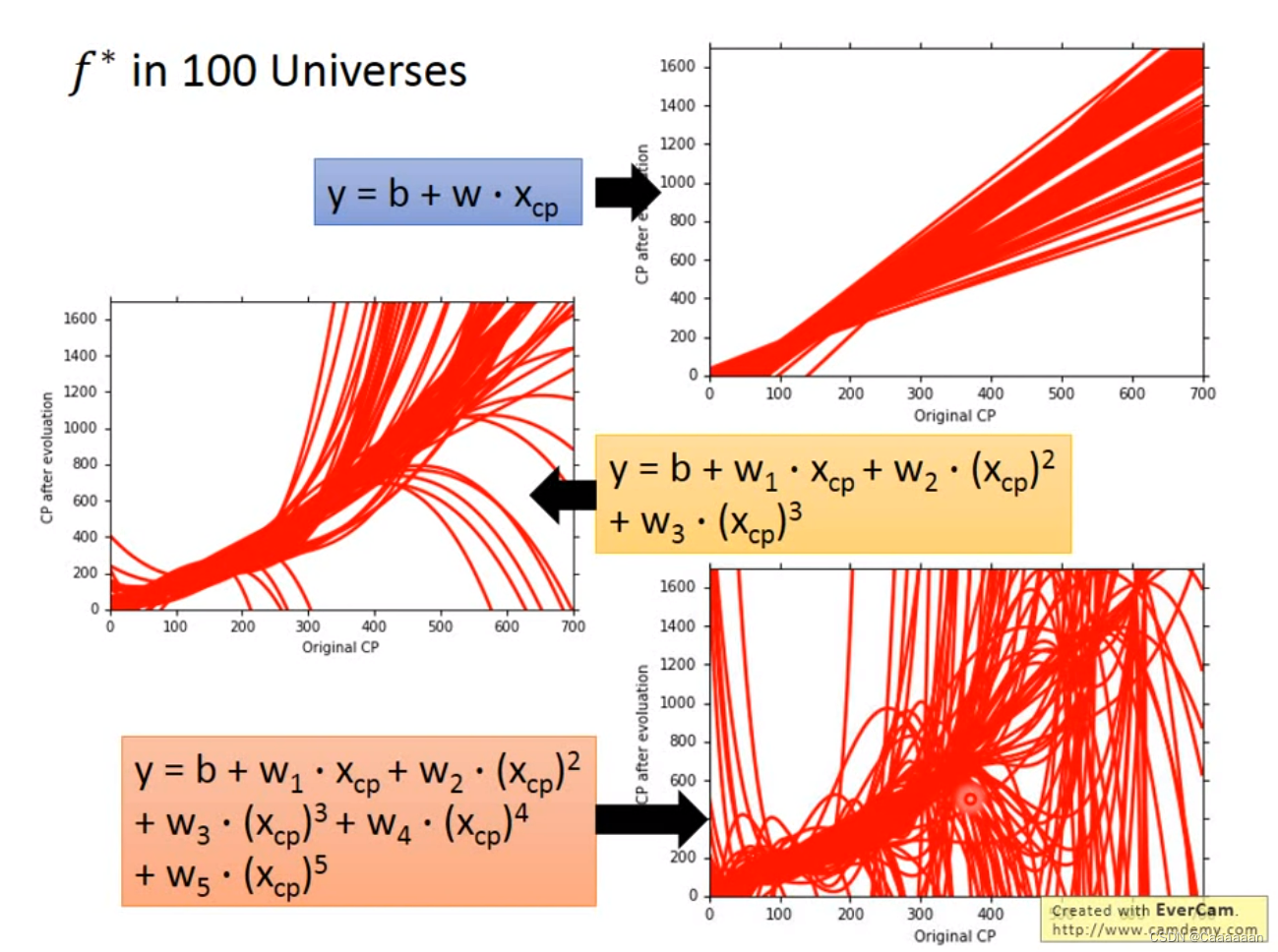
Variance

——简单的model具有比较小的Variance
——复杂的model往往具有比较大的Variance
Simpler model is less influenced by the sampled data
Bias
——你的所有 f ∗ f^* f∗ 的平均值——离你的 f ^ \hat{f} f^ 有多近,越近Bias越小

——简单的model具有比较大的Bias
——复杂的model具有比较小的Bias
因为简单的model的function set的范围很小,不一定能把target包含在内,target不在内的时候,无论你的function怎么sampled,都是不太好的

Bias v.s. Variance
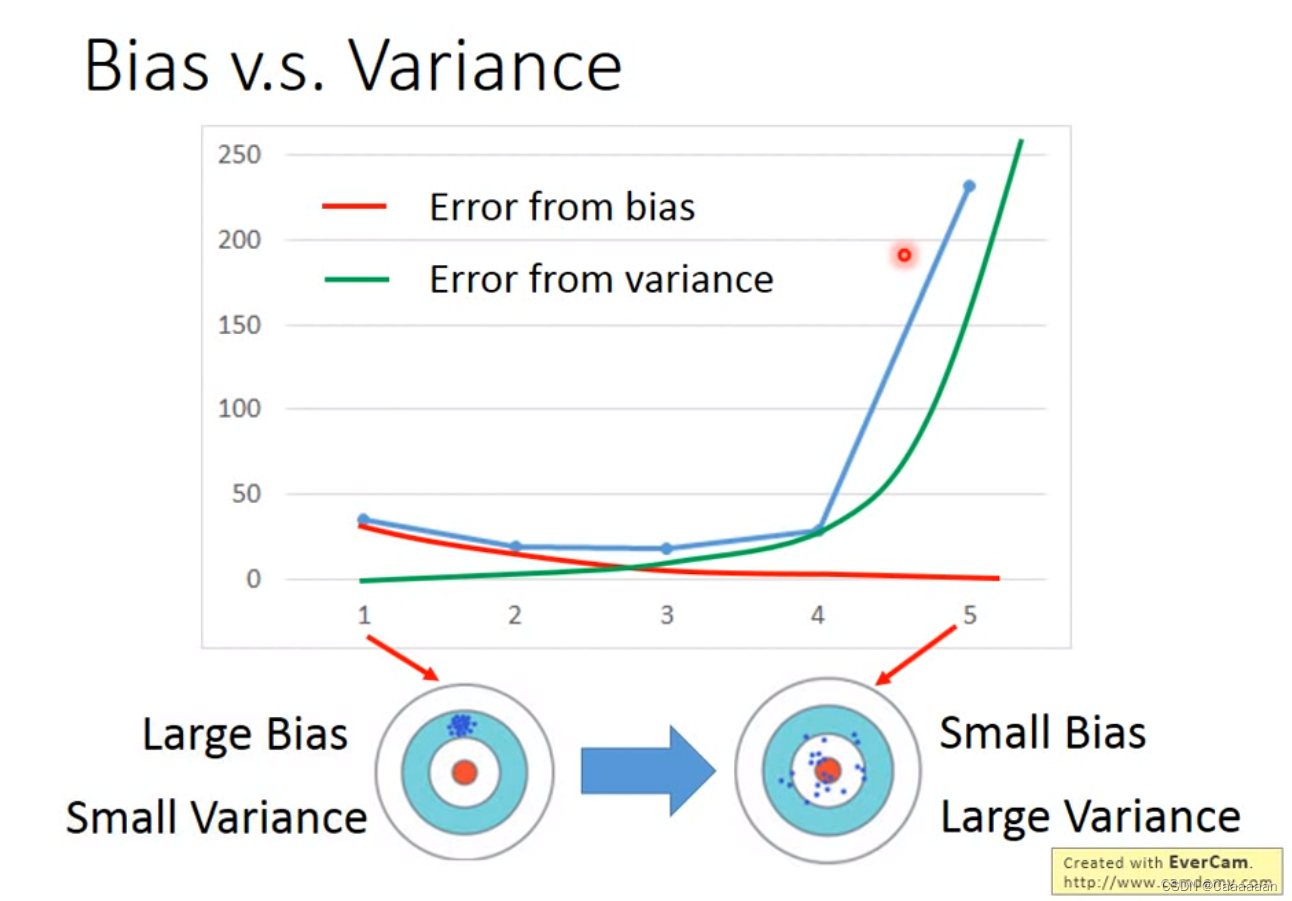
如果你的函数的error大部分来自variance,那么这个时候,呈现出来的就是过拟合(Overfitting)
如果你的函数的error大部分来自bias,那么这个时候,呈现出来的就是欠拟合(Underfitting)
- 如果你的模型,不能很好的fit训练集,就是UnderFitting
- 如果你的模型,在训练集上error很小,但是测试集的error很大,这个时候是Overfitting
Solve
-
对于很大的Bias,你需要做的是redesign你的模型
- 增加更多的输入特征
- 采用更复杂的模型
-
对于很大的Variance
-
增加更多数据
- 收集难——generate假的training data
-
正则化——Regularization
会使得曲线变得平滑——提高鲁棒性
-

——收集更多的数据,不会伤害Bias
——但是,正则化,相当于调整的function space,因此有可能会伤害你的Bias
Model Selection
- There is usually a trade-off between bias and variance.
- Select a model that balances two kinds of error to minimize total error.
交叉验证
进行Cross Validation获得最优的model

多折交叉验证
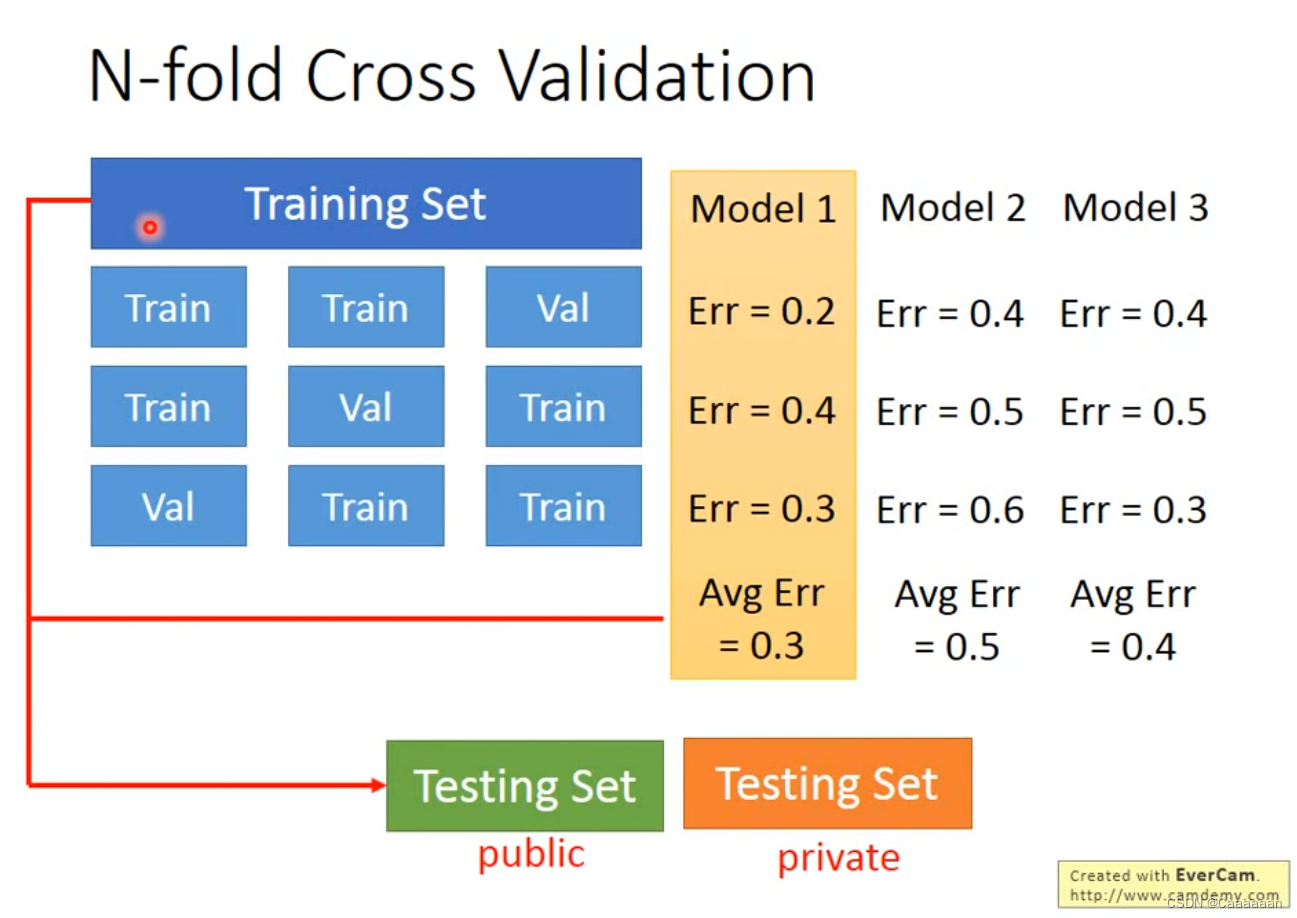
-
-
相关阅读:
我的Quick Latex For Obsidian-Setting(持续更新)
模型压缩(二)yolov5剪枝
IOS渲染流程之提交图层数据至RenderThread进程
九、数据仓库详细介绍(元数据)
类与对象(中)--六大默认函数--重点
SpringBoot整合篇 04、Springboot整合Redis
实现logstash从rabbitmq取数据存elasticsearch
Redis基于布隆过滤器解决缓存穿透问题(15)
(万字详解)MySQL增删改查(基础+进阶)
在微信小程序中怎么做投票活动
- 原文地址:https://blog.csdn.net/Hacker_ccc/article/details/126918342