时间序列分析|数据裁剪和滚动异常值检测

前言

在上一篇 《时间序列分析|异常值检测》 一文中，我们介绍了如何利用TSOD模块对5类异常值进行检测，这一篇我们将要介绍如何利用时序本身计算出来的统计量进行时序数据裁剪，滚动异常值检测。

先看数据

我们还是以air_passenger数据集为对象进行演示，先来看一下原数据长什么样子并对其进行可视化

import datetime
import time
import tsod
import pandas as pd
import pmdarima as pm
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from sklearn.metrics import mean_absolute_error 
from tsod import RangeDetector,GradientDetector,ConstantGradientDetector,RollingStandardDeviationDetector,DiffDetector

air_passenger = pd.read_csv(r"D:\项目\时间序列\air_passenger.csv") #读取数据
air_passenger['date'] = pd.to_datetime(air_passenger['date']) #datetime格式化

fig = plt.figure(figsize = (6,4)) #新建6*4的画布
plt.plot(air_passenger['date'],air_passenger['passenger'] ,label = 'ts_origin') #原时序图
plt.xticks(rotation =45) #横坐标逆时针倾斜45度
plt.legend() 
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

原数据就2列，一列是date，一列是passenger， 以date为横坐标，passenger为纵坐标，绘制出air_passenger的时序图，从air_passenger时序图我们看到序列的时间跨度是从2019年09月之前开始一直到2022年09月，中间有4段处于停飞状态，2020年05月到2020年09月中间有一段至暗时期，人数跌落到50人以下，姑且称为波谷，但是再2021年05月到2021年09月有一段高光时期，人数突破了200大关，暂称为波峰，除去这两段时期外，其余大部分位于150上下波动，且波动幅度不是特别大，那么我们可以预判这些为平稳时期表现，其余的如波峰，波谷，停飞期都可视为异常片段或者异常点，异常片段就是异常点形成聚集效果的时间段，现在要想办法将其甄别出来并适当剔除。

数据裁剪

数据裁剪是指对整个时序进行切片，保留那些正常的可为建模利用的时序片段。有时候，整个时序中会存在大时间跨度的空缺从而导致时序不连贯，姑且称为空档期，因为空挡期的前后时序的特征极有可能发生的特征迁移，如上图的2020年7月到2021年7月，时序就发生了特征迁移，假如利用空档期前时序进行训练，肯定不能用于空挡期后序列的预测，假如将空缺期前后序列混在一起进行训练的话，势必带来大量噪声，这对时序分析是大忌，如果整个时序观测点，特别是空档期后面的观测样本点比较丰富，完全可以进行时序截取，只保留空档期后面的时序进行训练和测试，下面我们就针对这种情况进行数据截取演示。

首先，我们需要把那些空档期找出来，为此，定义一个时间跨度的度量date_diff, 其计算方法就是date的向前一阶差分序列，即用date列的后面一个值减去前面一个值求得相邻两个date的时间差。

$$date[i+1]-date[i],foriindatelist$$

air_passenger = air_passenger[["date", "passenger"]].sort_values(by="date") #按日期升序排序
air_passenger['day_diff'] = [16]+[(air_passenger['date'].tolist()[i+1] - air_passenger['date'].tolist()[i]).days for i in range(len(air_passenger)-1)] #计算天数差
leap_point = [air_passenger['date'].tolist()[i]  for i in range(len(air_passenger)) if air_passenger['day_diff'].tolist()[i]>15] #时间跳跃点

print(air_passenger, leap_point)
1
2
3
4
5

这样，我们就多了一列air_passenger[‘day_diff’]用来表示时间差，为了数据对齐，我们在最前面加了一个单位长度的列表[16]拼接而成，这里的16可依据业务场景而定，因为我这里认为半个月(15天)停飞就是很不正常了，所以一切大于15天的都会被识别为空档期，设置为16恰好比半个月多一天，自然会被识别出来; 并且可以将这些空档期的日期leap_point(跳跃点)挑出来做成一个列表。

        date  passenger  day_diff
0   2019-06-30        153        16
1   2019-07-07        154         7
2   2019-07-14        156         7
3   2019-07-21        158         7
4   2019-07-28        152         7
..         ...        ...       ...
405 2022-08-29        142         2
406 2022-08-30        155         1
407 2022-09-01        185         2
408 2022-09-03        147         2
409 2022-09-05        132         2

[410 rows x 3 columns] [Timestamp('2019-06-30 00:00:00'), Timestamp('2019-10-27 00:00:00'), Timestamp('2020-05-18 00:00:00'), Timestamp('2021-03-28 00:00:00'), Timestamp('2022-07-09 00:00:00')]
1
2
3
4
5
6
7
8
9
10
11
12
13
14

我们看到一共有5个leap_point, 分别是2019-06-30，2019-10-27，2020-05-18，2021-03-28，2022-07-09，对应图中空档期的尾巴，现在只要把所有跳跃点都裁剪掉便得到后面的不含空档期的时序了，完成了数据裁剪。

ts_without_gap = air_passenger[air_passenger['date']>=leap_point[-1]] #取最近一个时间跳跃点后面的时序

fig = plt.figure(figsize = (6,4)) #新建6*4的画布
plt.plot(ts_without_gap['date'],ts_without_gap['passenger'] ,label = 'ts_without_gap') #原时序图
plt.xticks(rotation =45) #横坐标逆时针倾斜45度
plt.legend() 
plt.show()
1
2
3
4
5
6
7

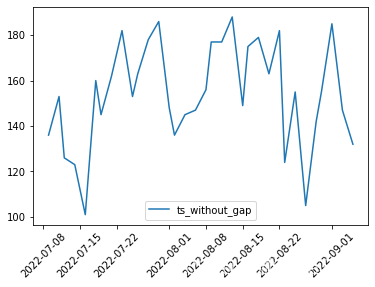
由上图我们可以看到，裁剪后的时序是从2022-07-09开始的，这段时序还是比较正常的，连贯且没有跳跃点，可以作为后续训练时序模型的原数据。

滚动异常检测

上一文在RollingStandardDeviationDetector检测一节中说过滚动标准差检测是以某个固定的滚动窗口进行向前滚动统计其均值和标准差，这完全可以用rolling函数把滚动均值算出来，然后将其标准差计算出来，规定其上下几倍个标准差的即为正常范围，超出这个范围的即认为是异常值。

air_passenger.set_index("date", inplace = True) #重置索引, 将date_设置为索引index
ts = air_passenger["passenger"] #乘客人数序列
print("原序列\n", ts)
ts_rolling = ts.rolling(window = 7).mean() #7阶截尾滑动平均
ts_rolling_std = ts_rolling.std() #标准差
# print("滑动平均:\n", ts_rolling, ts_rolling_std)
upper = (lambda x, y: x>y+1.5*ts_rolling_std)(ts, ts_rolling)
lower = (lambda x, y: x<y-1.5*ts_rolling_std)(ts, ts_rolling)
# print(upper, lower)
ts_filter = ts.drop(labels = ts[upper].index) #去上异常值
ts_filtered = ts_filter.drop(labels = ts[lower].index)#去下异常值
print("过滤后序列\n", ts_filtered)
plt.plot(ts, color = 'red', alpha = 1.0, label = 'ts_origin') #原序列
plt.plot(ts_rolling,   color = 'blue', alpha = 0.8, label = 'ts_rolling',) #移动平均序列
plt.plot(ts_filtered, color = 'green', alpha = 0.5,label = 'ts_filtered') #过滤后序列
plt.fill_between(ts_rolling.index, ts_rolling-2*ts_rolling_std, ts_rolling+2*ts_rolling_std, color='yellow', alpha= 0.2)
plt.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

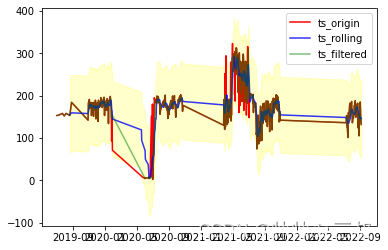
从上图可以看到那些超出来的红色样本就是异常值了，透明度为0.2的黄色便是滚动均值的1.5倍标准差可行范围，也只有红色曲线超出了这个范围，便可以将其过滤掉，过滤后样本点由原来的410个减少到385个，减少了一些噪声点。

至此，我们完成了时间序列的裁剪工作和利用滚动均值和标准差进行异常值检测。

参考文献

1，时间序列分析|异常值检测