FAIG滤波器

还是搬运者学习记 一切感恩于大佬

单分支网络如何自动学习区分退化？本文提出了一种盲超分网络解释的方法 FAIG，一种基于积分梯度的对 Filter 进行归因的方法。

发现盲超分模型中具有特定退化作用的滤波器

论文名称：Finding Discriminative Filters for Specific Degradations in Blind Super-Resolution (NeurIPS 2021)

论文地址：https://arxiv.org/pdf/2108.01070.pdf

盲超分任务介绍

作为基本的 low-level 视觉问题，单图像超分辨率 (SISR) 越来越受到人们的关注。SISR 的目标是从其低分辨率观测中重建高分辨率图像。目前已经提出了基于深度学习的方法的多种网络架构和超分网络的训练策略来改善 SISR 的性能。顾名思义，SISR 任务需要两张图片，一张高分辨率的 HR 图和一张低分辨率的 LR 图。超分模型的目的是根据后者生成前者，而退化模型的目的是根据前者生成后者。经典超分任务 SISR 认为：低分辨率的 LR 图是由高分辨率的 HR 图经过某种退化作用得到的，这种退化核预设为一个双三次下采样的模糊核 (downsampling blur kernel)。 也就是说，这个下采样的模糊核是预先定义好的。但是，在实际应用中，这种退化作用十分复杂，不但表达式未知，而且难以简单建模。 双三次下采样的训练样本和真实图像之间存在一个域差。以双三次下采样为模糊核训练得到的网络在实际应用时，这种域差距将导致比较糟糕的性能。这种退化核未知的超分任务我们称之为盲超分任务 (Blind Super Resolution)。

盲超分任务的退化方式有很多种, 比如模糊 (blur), 噪声 (noise) 或者下采样 (downsampling) 等。令  和  分别代表  和  图片, 退化模型为:

式中,  代表卷积操作, 模型主要由3部分组成: 模糊核 , 下采样操作  和附加噪声  。前人工作中最广泛采用的模糊核是各向同性高斯模糊核 (isotropic Gaussian blur kernel)。  一般为加性白高斯噪声 (Additive White Gaussian Noise, AWGN)。Blind SISR 任务就是从 LR 图片恢复  图片的过程。

盲超分模型的两种模式

盲超分模型有单分支网络 (One-branch Network) 和双分支网络 (Two-branch Network) 两种模式，在之前我介绍的工作中：

超分辨率超详细解读

(一)：模糊核迭代校正盲超分方法 IKC 超分辨率超详细解读

(二)：盲超分的端到端交替优化方法 DAN

 

IKC 和 DAN 这两个盲超分方法，以及 DASR[1]等等，都属于下图1中的双分支网络。图1中还有一种单分支网络。

双分支网络的其中一个分支A一般用于预测模糊核 (degradation prediction)，另一个分支B根据分支A所预测的模糊核重建 SR 图像 (conditional restoration)。 这种设计结合了一些退化过程的人类先验知识，因此具有一定程度的可解释性。

那么单分支网络能不能很好地完成盲超分的任务呢？单分支网络没有模糊核预测这一步，那么它能不能在缺乏人类先验知识的情况下完成这个任务呢？

对于两种最先进的盲超分模型：DAN 和 DASR，作者对比了它们的双分支网络版本和单分支网络版本的性能。

对于双分支网络，使用相应的官方发布的代码进行的，除了网络结构之外，其他设置都保持不变。

对于单分支网络，使用 SRResNet 作为模型。作者调整残差块的数量，以匹配双分支网络和单分支网络相似的计算复杂度 (FLOPs 和 Params.)。退化核使用 blur 和 blur+noise 两种情况，PSNR 的比较如下图2所示。作者发现在相似的计算复杂度下，双分支网络版本和单分支网络版本性能差距不大，这一有趣的观察促使作者去研究盲超分网络，尤其是单分支网络的潜在机制。whaosoft aiot http://143ai.com 

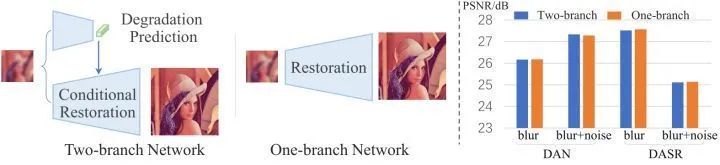
图1：左：盲超分的双分支网络和单分支网络。右：对于最先进的盲超分方法 DAN 和DASR，对应的单分支网络可以在类似的计算预算下实现可比的性能。

图2：盲超分任务中双分支和单分支网络的 PSNR (RGB通道) 对比

双分支网络具有更高的可解释性。尽管单分支和双分支网络的性能相当，但是单分支网络更像一个 "黑盒"，我们很好奇它与双分支网络的联系。 具体来说，上面的现象使作者提出两个关键问题：

1. 单分支网络能够自动学习得像双分支网络那样具有区分不同退化作用的能力吗？

2. 对于某种特定的退化作用，单分支网络是否存在一个子网络专门负责这种特定的退化作用？

在 Filter 维度使用积分梯度进行归因分析

积分梯度

积分梯度代表了图像中的每个像素对最终输出结果的 "贡献度大小" 或 "影响程度"。

假设我们要分析的输入是 , 还有一个基线图片是 , 可以取纯黑的图片等等。模型是 , 假设是个分类模型或者  模型,  是插值参数，  表示从基线图片  到原始输入图片  的揷值过程。则积分梯度 (Integral Gradient) 的定义为：

其中,  的含义是输入图片  的第  个像素对最终输出结果的 "贡献度大小" 或 "影响程度"。

积分梯度满足所有分量的积分梯度之和等于从基线图片到最终图片模型输出结果的变化:

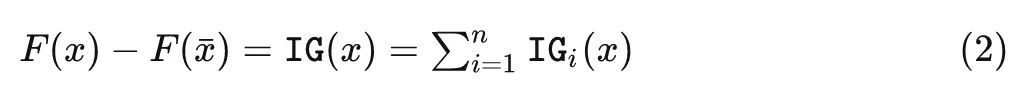
积分梯度可以通过找出解释网络预测结果的最重要的输入像素或输入特征来解释深度神经网络。

在 Filter 维度使用积分梯度进行归因分析

传统的积分梯度方法是找出对于网络预测结果的最重要的输入像素或输入特征。本文作者试图找到对于盲超分网络特定的消除退化作用 (比如去模糊，去噪等等) 的最重要的那些 Filter (这里 Filter 的定义是一个  的卷积核) ，也就是在 Filter 维度使用积分梯度。因此本文方法叫做 "在 Filter 维度使用积分梯度进行归因分析" Filter Attribution Integrated Gradients (FAIG)。

下面两段话是本文的核心思想：

• 积分梯度方法 (IG) 有个基线输入图片，它是一张纯黑的图片，分类模型的输出结果没有任何含义。目标图片是有意义的输入图片 (比如一张 dog 的图片)。积分梯度使输入从基线图片逐渐过渡到目标图片，输出也从无意义的输出结果 (分类结果无意义) 过渡到有含义的结果 (比如分类结果为 dog 类别)。那么这个过程中每个像素的积分梯度就代表这个像素对结果的 "贡献度"。

• 本文方法 (FAIG) 有个基线网络，它是一个不能消除任何退化作用的纯 SR 网络 (不是盲超分网络)，网络本文只有超分功能，没有任何消除退化 (degredation) 的功能。目标网络是一个可以处理复杂退化的盲超分网络。积分梯度使输入从基线网络逐渐过渡到目标网络，模型的功能也从单纯的超分功能过渡到有同时具备消除退化的功能和超分功能。给定相同的输入，网络输出的变化可以归因于网络参数 (即 Filter) 的变化。 那么这个过程中每个 Filter 的积分梯度就代表这个 Filter 对网络功能变化的 "贡献度"。

令  代表具有去退化作用的盲超分网络, 输入图片为 , 网络参数为  。使用下式来量化网络的功能:

式中,  是 HR 图片,  衡量了网络输出和真值之间的差距。距离越短, 表示网络 degredation 的功能越强。

我们令  为积分梯度的路径,  分别代表了模型的起点 (纯超 分模型) 和终点 (盲超分模型)。

对于任意的输入图片 , 模型从纯超分模型沿路径  变化为盲超分模型, 网络输出和真值之间的差距也会越来越小。这一过程的积分梯度可以写成：

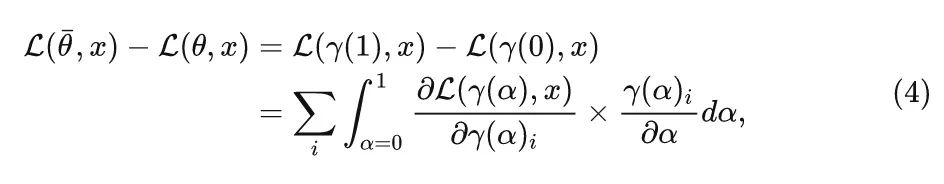
所以, 模型的第  个 Filter 对最终输出结果的 "贡献度大小" 或 "影响程度" (即  ) 可以表示为:

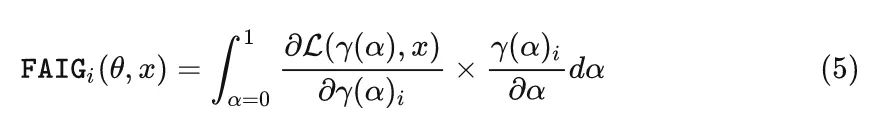
以上就是 FAIG 的思想，它对网络参数进行积分梯度，来识别到底是哪一个 Filter 的参数对模型的去退化功能起了作用。

基线模型和积分路径

基线模型

在 FAIG 思路的基础上，作者认为基线模型应该具有下面的性质：

1. 基线模型相比于目标模型，应该刚好缺失了某种特定的去退化功能 (如去噪等) ，其他功能 (如超分等) 保持不变。

2. 基线模型应该与目标模型应该有完全相同的输入图像。

3. 基线模型应该与目标模型的参数 "差不多"，这样这些与特定去退化功能有关的特定的 Filter 就不会太多。

为了得到这么一组模型 (基线模型和目标模型)，作者采用了一种 Fine-tuning 的办法。首先训练一个普通的超分网络，它只能够处理双三次下采样核，没法处理模糊核引起的模糊和噪声等的退化作用。再对其进行 Fine-tuning ，使之具备这种处理模糊，噪声等等的能力。

积分路径

积分路径采用简单的线性插值，和积分梯度方法一致。

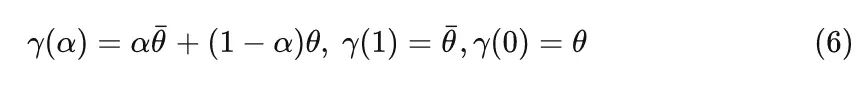
因此，上式5可以重写为：

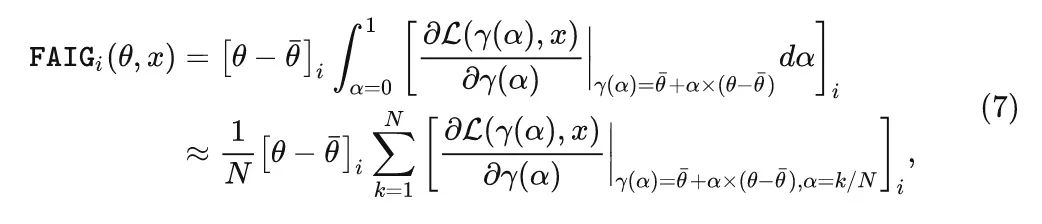
式中， NN 是用累加近似代替积分的步数，本文取100。

问：为什么不直接计算目标网络和基线网络的参数之差 ？

答： 这种方法没有考虑对网络输出的影响，因为参数的变化可能导致的并不是使网络丧失了某种去退化的功能，而是其他方面的功能。所以直接参数相减，我们就没办法去研究到底是哪些参数负责了网络的某种特定的退化功能。

 通过 FAIG 发现盲超分模型中具有特定退化作用的滤波器

上面的 FAIG 方法能够找到模型中对于某种特定的退化作用非常重要的 Filter，但是也有2个缺点：

1. FAIG 方法确实能够找到负责某种去退化作用的 Filter，但是这些 Filter 除了负责这种去退化，可能还负责其他的去退化作用。

2. 上式7还与输入图片有关。其实若想找到负责某种去退化作用的 Filter，方法应该与输入图像内容无关。

所以作者这里做了两个改进：

一是把上式7的计算方法改为：

其中,  代表某一种退化作用, 而  代表其他退化作用。这个改进就是想选择出对某一种退化作用 FAIG 值大的 Filter 而对其他的退化作用 FAIG 值小的 Filter。

而是对整个数据集  中的所有 FAIG 梯度差进行平均, 以消除图像内容的影响。

 

FAIG 的附加功能：预测输入图片的退化类型

FAIG 的附加功能是预测输入图片的退化类型。基于 FAIG 发现的对某种特定的退化作用有效的 Filter，我们就能够判断任意输入图片的退化类型。

假设  filter  为由8式得到的负责去掉  这种退化作用的 Filter, {filter  为8由式得到的任意输入图片的 Filter, 则计算重叠分数 (OS) 来衡量两组 Filter 的交集：

较高的重叠分数  表示输入图像  的退化作用更类似于退化作用  。因此, 我们能够通过将  与不同退化的阈值  进行比较来预测输入图像的退化。阈值可以由验证数据集来确定。

 实验结果

网络架构：

1) SRCNN-style 网络架构： 有9层卷积，最后是上采样层。

2) SRResNet 网络架构： 不包含 BN 层的SRResNet 网络，带有残差连接。

退化核：

双三次下采样 scale=2，高斯模糊核  ，高斯噪声 level=1。

作者按照1式生成退化的图像。高斯模糊和高斯噪声是以0.5的概率独立使用的。

数据集：

训练集：使用了 DIV2K training dataset，有800张高清的 HR 图。

验证集：Set14，BSD100，和 DIV2K validation set (100 images)

训练策略：

首先训练一个普通的 SR 模型作为前文提到的基线模型，之后再 Fine-tune 这个模型使之具备去退化 (去噪，去模糊) 的功能。使用 Adam 优化器训练 100K iteration。

实验验证1："屏蔽" FAIG 发现的 Filters 的功能

FAIG 的实验验证方法是：FAIG 会首先发现一些负责某些特定退化作用 (假设是模糊) 的 Filter。那么目标盲超分模型  当中的这些 Filter 对这些特定的退化作用而言是十分重要的。那么如果我们现在用基线模型  当中的这些 Filter 来替换它们，那么我们就会得到一个全新的模型。

此时，我们就用模糊的图片来输入这个全新的模型，看看输出结果还有没有模糊了。如果出现了模糊的话，那证明 FAIG 确实检测到了负责去模糊作用的 Filter；如果依旧未出现模糊，那证明 FAIG 检测到的这些负责去模糊作用的 Filter 是假的。这种验证方法称之为 "屏蔽" 发现的 Filters 的功能。

因此，我们就可以通过测量目标模型  和基线模型  的输出差异 (例如 MSE) 来量化发现的 Filter 对网络函数的贡献。

为了减少亮度和对比度变化的影响，作者计算了灰度图像梯度的输出差异。如果存在较大的差异，则表示FAIG 确实检测到了负责去模糊作用的 Filter。

如下图3所示是本实验的结果。图3的上面2幅图是我们替换掉 FAIG 发现的负责去模糊的 Filter 之后的新模型与原始盲超分模型 FF 的性能之差，图3的上面2幅图是我们替换掉 FAIG 发现的负责去噪声的 Filter 之后的新模型与原始盲超分模型  的性能之差。

我们可以发现：

当我们替换掉 FAIG 发现的负责去模糊的 Filter 之后，对于模糊的输入图片，新模型相比于原始盲超分模型  ，性能急剧下降；但对于含噪声的输入图片，新模型相比于原始盲超分模型  ，性能却更有优势。

当我们替换掉 FAIG 发现的负责去噪声的 Filter 之后，对于含噪声的输入图片，新模型相比于原始盲超分模型  ，性能急剧下降；但对于模糊的输入图片，新模型相比于原始盲超分模型  ，性能却更有优势。

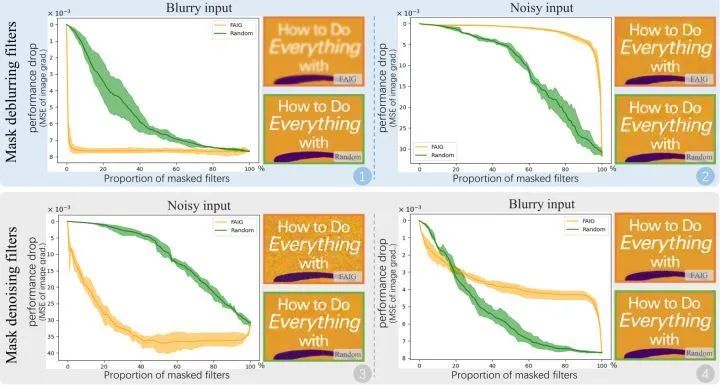
图3：实验验证：用不同比例（在 SRResNet 上）屏蔽发现的 Filters 的功能

如下图4所示，对于一张模糊的输入①一张含有噪声的图⑤，盲超分网络的输出分别是②和⑥，都实现了去退化的效果。当我们使用 FAIG 的方法盖住1%的去模糊 Filter 时，对于模糊输入而言，模型丧失了去模糊的功能，结果是③。对于含噪声的输入而言，模型并未丧失去噪的功能，结果是⑦。当我们使用 FAIG 的方法盖住1%的去模噪声 Filter 时，对于含噪声输入而言，模型丧失了去噪的功能，结果是⑧。对于模糊的输入而言，模型并未丧失去模糊的功能，结果是④。

图4：盖住1%的去特定退化作用的 Filter 时，看网络性能的变化

如下图5所示，作者还对比了类似的方法 IntInf 等，也发现 FAIG 发现的 Filter 可以发现导致最大的性能下降，证明 FAIG 发现的 Filter 对于特定的退化作用的有效性。

图5：量化对比

实验验证2：只重新训练 FAIG 发现的 Filters

为了进一步验证 FAIG 发现的 Filter 对于盲超分网络特定任务的作用，作者想探究发现的这些 Filter 的位置及其连接对于网络而言是否重要。因此作者做了这样一个实验：先拿基线模型 F(\bar{\theta})F(\bar{\theta}) ，它只具有普通的 SR 功能，而没有盲超分的功能。现在只训练 FAIG 发现的 Filters，其他 Filter 参数固定住，看看网络会不会因此具有盲超分的能力。

作者比较了不同方法重新训练的模型的 PSNR，选择重新训练的 Filter 的方式有4种：1) FAIG，2) IntInf，3) \left| \theta-\bar{\theta} \right|\left| \theta-\bar{\theta} \right| ，4) 随机选择。结果如下图6所示。FAIG 发现的针对去模糊的 Filter，在重新训练之后，模型去模糊的性能上涨很多，去噪的性能一般；FAIG 发现的针对去噪声的 Filter，在重新训练之后，模型去噪的性能上涨很多，去模糊性能一般；其他方法发现的 Filter 重新训练之后模型的性能比随机选择的 Filter 更差。作者推测，这些方法发现的位置和连接可能会阻碍重新训练过程。这说明 FAIG 所发现的滤波器的权重，位置和连接都是重要的。

图6：不同方法重新训练的模型的 PSNR

作者也观察了 FAIG 发现的负责不同的退化作用的 Filter 在模型中的位置分布，如下图7所示，作者可视化了针对不同的退化作用发现的1%的滤波器的位置。得出的结论是：用于去模糊和去噪的滤波器在网络内部具有非常不同的分布。负责去模糊滤波器更多地位于网络的后部，而负责去噪的滤波器分布更加均匀。因此作者推测，负责去模糊滤波器需要更大的感受野。而且，它们的互补分布也隐含着网络中的分工。

图7：FAIG 发现的负责不同的退化作用的 Filter 在模型中的位置分布

FAIG 的缺点是： 1) FAIG 考虑的退化作用是模糊，噪声等等独立的退化作用，但是实际场景的退化作用是复杂且未知的。2) FAIG 分析的网络架构只有 SRCNN-style 和 SRResNet，没有其他含有 attention 或者 non-local 架构的模型。3) FAIG 的发现距离指导盲超分网络的设计还有一点差距。但是，利用盲超分网络的可解释性将对未来设计更有效的体系结构和诊断盲超分网络具有重要意义，如确定网络恢复能力的边界或者提高算法的鲁棒性。

总结

本文提出了一种盲超分网络解释的方法 FAIG，一种基于积分梯度的对 Filter 进行归因的方法。FAIG 认为一个单分支的盲超分模型中特定的滤波器负责特定的去退化作用，有些 Filter 负责去模糊，有些负责去噪等等。 基于所提出的 FAIG，作者能够为盲超分中的特定退化作用找到与之对应的非常少量 (至少1%) 的 Filter。 所发现的滤波器的权重，位置和连接都是重要的。此外，退化的任务可以通过这些找到的特定的 Filter 隐式地实现，而无需显式的监督学习。 这个发现可以帮助我们更好地理解单分支盲超分网络的行为。 我们相信，利用盲超分网络的可解释性将对未来设计更有效的体系结构和诊断盲超分网络具有重要意义，如确定网络恢复能力的边界或者提高算法的鲁棒性。