-
《算法导论》第16章-贪心算法 16.1-活动选择问题(含C++代码)
一、问题背景
一个调度竞争共享资源的多个活动的问题,目标是选出一个最大的互相兼容的活动集合。假定有一个n个活动的集合S={a1, a2,…,an},这些活动使用同一个资源(例如一个阶梯教室),而这个资源在某个时刻只能供一个活动使用。
每个活动ai都有一个开始时间si和一个结束时间fi,其中0 ≤ si < fi <∞。如果被选中,任务ai发生在半开时间区间[si,fi)期间。如果两个活动ai和aj;满足[si,fi)和[sj,fj)不重叠,则称它们是兼容的。也就是说,若si≥fj或sj≥fi,则ai和aj是兼容的。
在活动选择问题中,我们希望选出一个最大兼容活动集。假定活动已按结束时间的单调递增顺序排序:

活动问题的最优子结构(可以仔细看书上原话)

这里可以通过动态规划来解决这个问题,如果用c[i,j]表示集合Sij最优解的大小,那么可以得到递归式

当然,在不知道ak的情况下,需要考查Sij中的所有活动,寻找最优解:

贪心选择
1、对于活动选择问题,什么是贪心选择?直观上,我们应该选择这样一个活动,选出它后剩下的资源应能被尽量多的其他任务所用。现在考虑可选的活动,其中必然有一个最先结束。因此,直觉告诉我们,应该选择S中最早结束的活动(它剩下的资源可供它之后尽量多的活动使用)(如果S中最早结束的活动有多个,我们可以选择其中任意一个)。
2、之后,只剩下一个子问题让我们求解:寻找在a1后开始的活动。
3、我们已经证明活动选择问题具有最优子结构性质。令kk={ai∈S: si≥fk}为在ak结束后开始的任务集合。当我们做出贪心选择,选择了a1后,剩下的S1是唯一需要求解的子问题。最优子结构性质告诉我们,如果an在最优解中,那么原问题的最优解由活动a1及子问题S中所有活动组成
4、如何确定我们直觉的正确性?
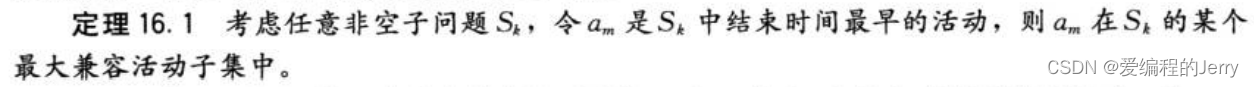
递归贪心算法
输入为两个数组s和f,分别表示活动的开始和结束时间,下标k指出要求解的子问题sk,以及问题规模n,其返回Sk的一个最大兼容活动集。假设活动已经按照结束时间进行了排序。为了方便初始化,添加一个虚拟活动a0。
RECURSIVE-ACTIVITY-SELECTOR(s,f,k,n) m = k+1 while m<=n and s[m]- 1
- 2
- 3
- 4
- 5
- 6
- 7

迭代贪心算法
GREEDY-ACTIVITY-SELECTOR(s,f) n = s.length A={a1} //将初值设置为只包含这个活动 k = 1 //设置为此活动下标 for m = 2 to n //寻找sk中最早结束的活动 if s[m]>=f[k] A=A∪{am} k=m return A- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
C++代码(递归版本)
#include#include #include using namespace std; vector<int> s = { 0,1,3,0,5,3,5,6,8,8,2,12 }, f = { 0,4,5,6,7,9,9,10,11,12,14,16 }; int RECURSIVE_ACTIVITY_SELECTOR(vector<int>& s, vector<int>& f, vector<int>& v_union, int k, int n) { int m = k + 1; while (m <= n && s[m] < f[k]) { m++; } if (m <= n) { v_union.push_back(m); return RECURSIVE_ACTIVITY_SELECTOR(s, f, v_union,m, n); } else { return 0; } } int main() { int n = 11; vector<int>v; RECURSIVE_ACTIVITY_SELECTOR(s, f, v,0, n); for (auto i : v) { cout << "a" << i << " "; } return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
C++代码(迭代版本)
#include#include using namespace std; vector<int> s = { 0,1,3,0,5,3,5,6,8,8,2,12 }, f = { 0,4,5,6,7,9,9,10,11,12,14,16 }; vector<int> Greedy_Activity_Selector(vector<int> const& s, vector<int> const& f) { int n = s.size() - 1; vector<int> A = { 1 }; int k = 1; for (int m = 2; m <= n; ++m) { if (s[m] >= f[k]) { A.push_back(m); k = m; } } return A; } int main() { vector<int> V = Greedy_Activity_Selector(s, f); for (auto& i : V) { cout << "a" << i << " "; } return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
毕设-基于SpringBoot学生住宿管理系统
细说react源码中的合成事件
涛思 TDengine 2.6+优化参数
机器学习笔记 - 感知器的数学表达
机器学习---使用 TensorFlow 构建神经网络模型预测波士顿房价和鸢尾花数据集分类
JSplacement丨随机生成置换贴图
windows域KCC知识点
git gitlab撤回已经提交的代码,回滚到某一个版本/节点
低功耗局域网通信硬件之lora——sx1262-sx1276硬件设计开发