-
Chapter7:非线性控制系统分析
基于胡寿松主编的《自动控制原理》(第七版)附录的 M A T L A B {\rm MATLAB} MATLAB控制系统简单教程,快速了解 M A T L A B {\rm MATLAB} MATLAB在控制理论的应用,下载链接: MATLAB辅助分析与设计方法基础.
7.非线性控制系统分析
-
微分方程高阶数值解法
命令格式:[t,x]=ode45('fun',t,x0) 参数说明: fun:调用函数; t:设定的仿真时间; x0:系统的初始状态;- 1
- 2
- 3
- 4
- 5
-
实例分析:非线性系统的稳定性分析
E x a m p l e B − 8 {\rm ExampleB-8} ExampleB−8: 设系统如下图所示,分别用描述函数法和相平面法判断系统的稳定性,并画出 c ( 0 ) = − 3 , c ˙ ( 0 ) = 0 c(0)=-3,\dot{c}(0)=0 c(0)=−3,c˙(0)=0,的相轨迹和相应的时间响应曲线。
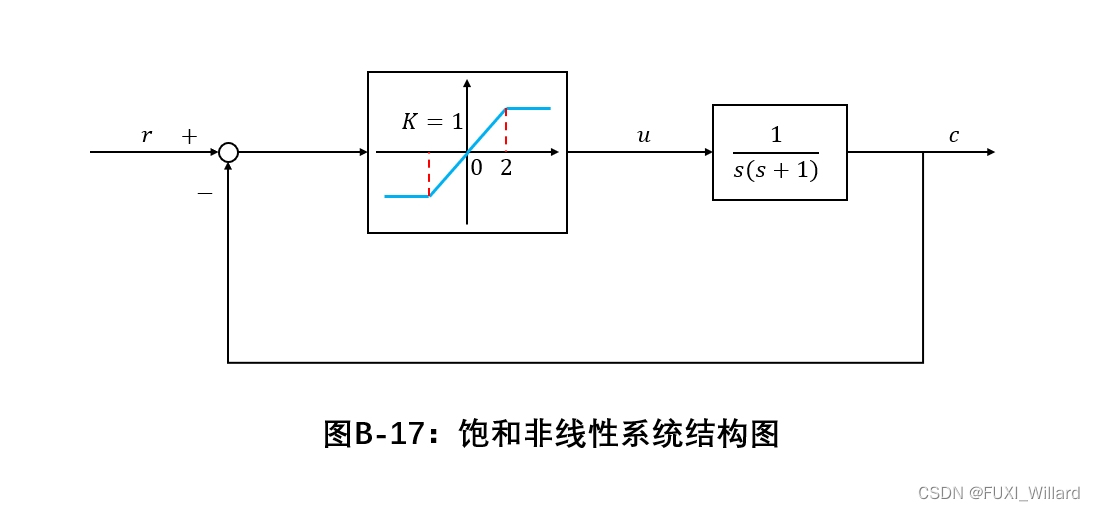
解:
【描述函数法】
非线性环节的描述函数为:
N ( A ) = 2 π [ arcsin 2 A + 2 A 1 − ( 2 A ) 2 ] , A ≥ 2 N(A)=\frac{2}{\pi}\left[\arcsin\frac{2}{A}+\frac{2}{A}\sqrt{1-\left(\frac{2}{A}\right)^2}\right],A≥2 N(A)=π2 arcsinA2+A21−(A2)2 ,A≥2
在复平面内分别绘制线性环节的 Γ G \Gamma_G ΓG曲线和负倒描述函数 − 1 / N ( A ) -1/N(A) −1/N(A)曲线,由于 G ( s ) G(s) G(s)为线性环节:
G ( s ) = − 1 N ( A ) G(s)=-\frac{1}{N(A)} G(s)=−N(A)1
利用频域奈氏判据可知,若 Γ G \Gamma_G ΓG曲线不包围 − 1 / N ( A ) -1/N(A) −1/N(A)曲线,则非线性系统稳定;反之,则非线性系统不稳定;% exampleB_8a.m G=zpk([],[0 -1],1); % 建立线性环节模型; nyquist(G);hold on % 绘制线性环节奈奎斯特曲线ΓG,图形保持; A=2:0.01:60; % 设定非线性环节输入信号振幅范围; % 计算负倒描述函数实部和虚部; x=real(-1./((2*(asin(2./A)+(2./A).*sqrt(1-(2./A).^2)))/pi+j*0)); y=imag(-1./((2*(asin(2./A)+(2./A).*sqrt(1-(2./A).^2)))/pi+j*0)); plot(x,y); % 绘制非线性环节的负倒描述函数; axis([-1.5 0 -1 1]);hold off % 重新设置图形坐标,取消图形保持;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
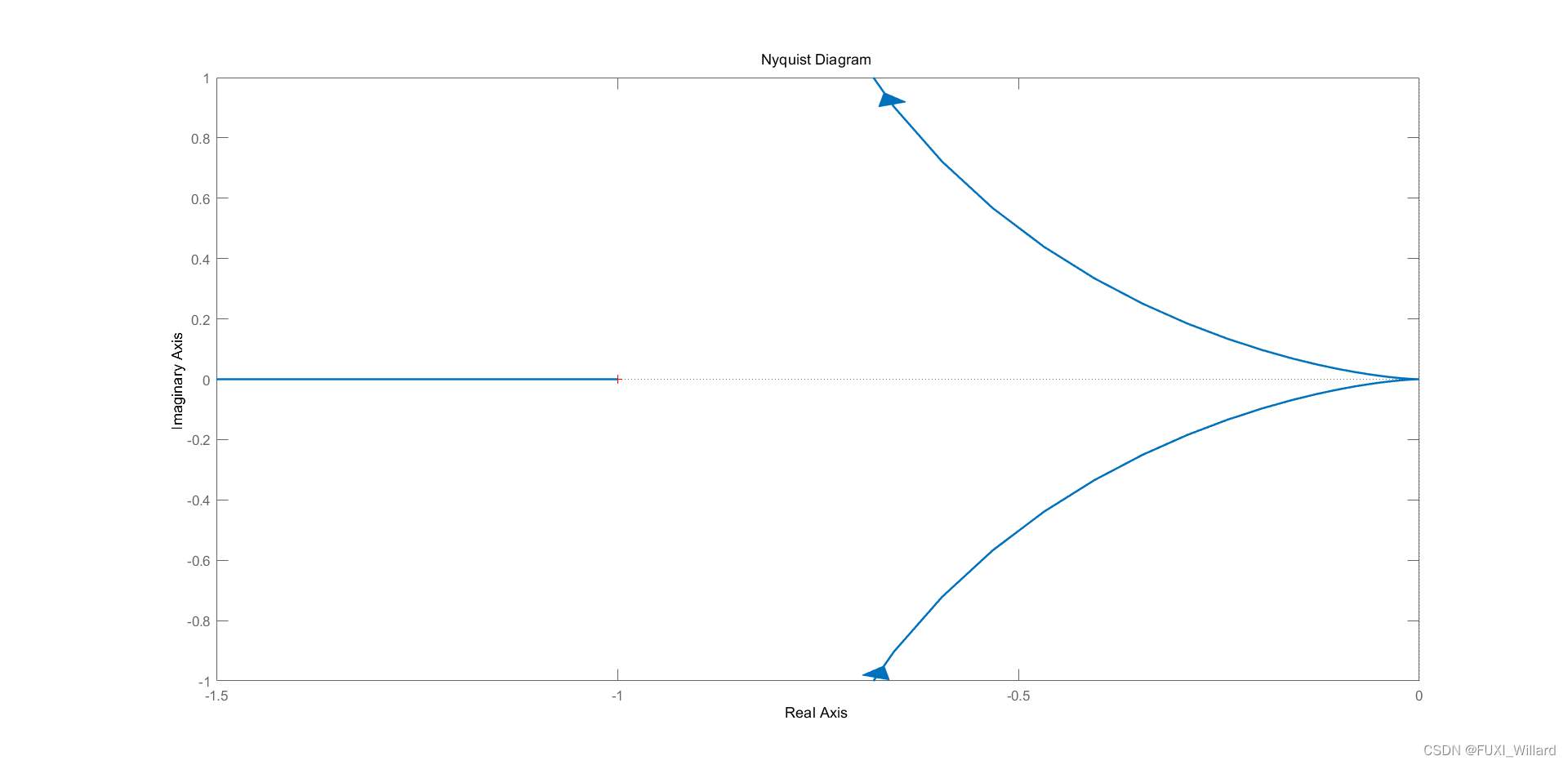
图中 Γ G \Gamma_G ΓG曲线不包围 − 1 / N ( A ) -1/N(A) −1/N(A)曲线,根据非线性稳定判据,该非线性系统稳定。
【相平面法】
描述该系统的微分方程为:
c ¨ + c ˙ = { 2 , c < − 2 − c , ∣ c ∣ < 2 − 2 , c > 2 \ddot{c}+\dot{c}=c¨+c˙=⎩ ⎨ ⎧2,−c,−2,c<−2∣c∣<2c>2{ 2 , c < − 2 − c , | c | < 2 − 2 , c > 2
在相平面上精确绘制 c − c ˙ c-\dot{c} c−c˙曲线,需要先确定上述系统微分方程在一定初始条件下的解,进而通过分析相轨迹的运动形式,直观地判断非线性系统的稳定性;% exampleB_8b.m t=0:0.01:30; % 设定仿真时间30s; c0=[-3 0]'; % 给定初始条件; [t,c]=ode45('fun',t,c0); % 求解初始条件下的系统微分方程; figure(1) plot(c(:,1),c(:,2));grid % 绘制相平面图,c(:,1)为c(t)值,c(:,2)为导数值; figure(2) plot(t,c(:,1));grid; % 绘制系统时间响应曲线; xlabel('t(s)');ylabel('c(t)');- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
% fun.m function dc=fun(t,c) % 描述系统的微分方程 dc1=c(2); % c1表示c(t),c(2)表示c(t)一阶导,d表示一阶导数; if(c(1)<-2) dc2=2-c(2); elseif(abs(c(1))<2) dc2=-c(1)-c(2); else dc2=-2-c(2); end dc=[dc1 dc2]';- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
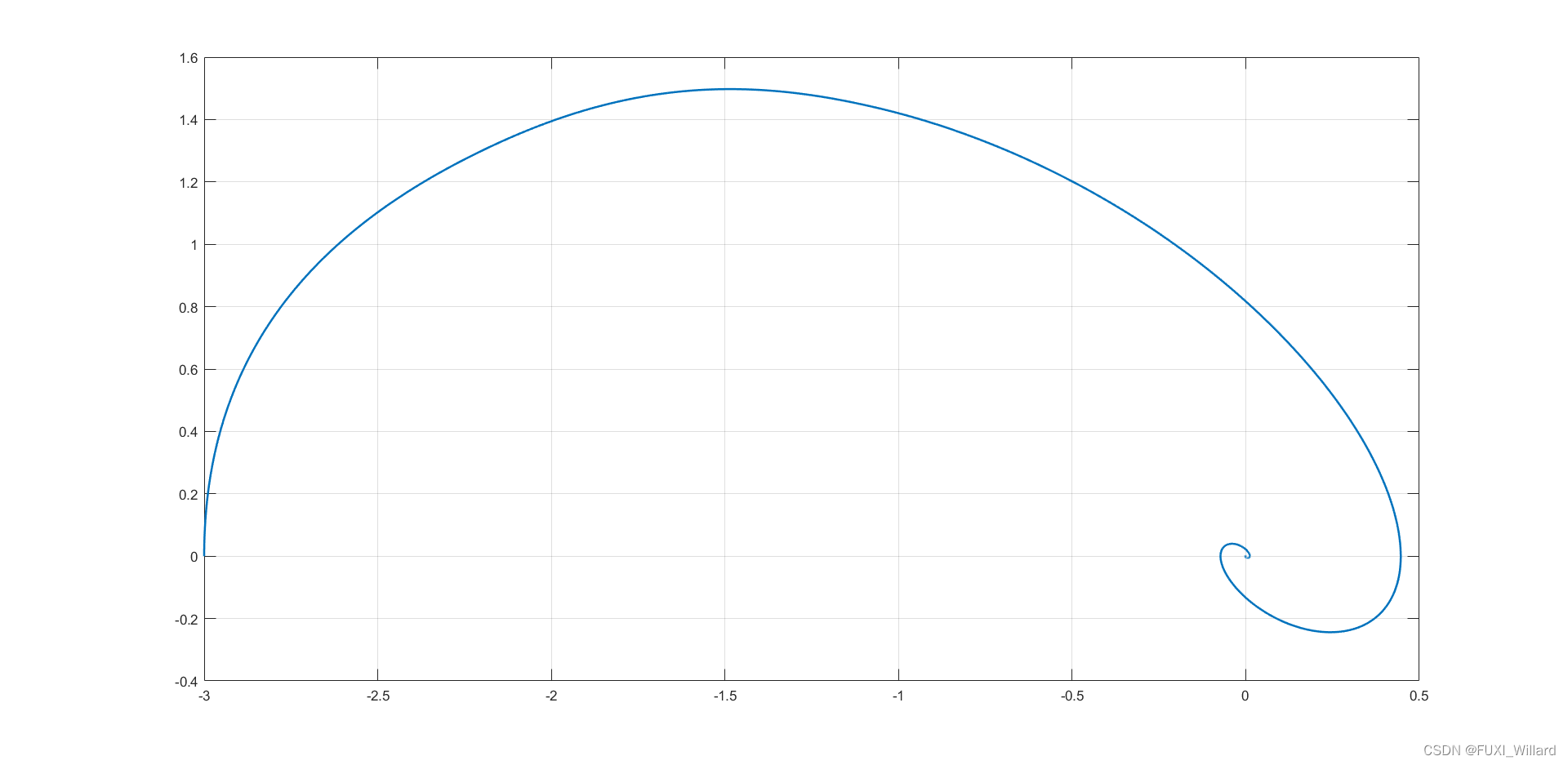
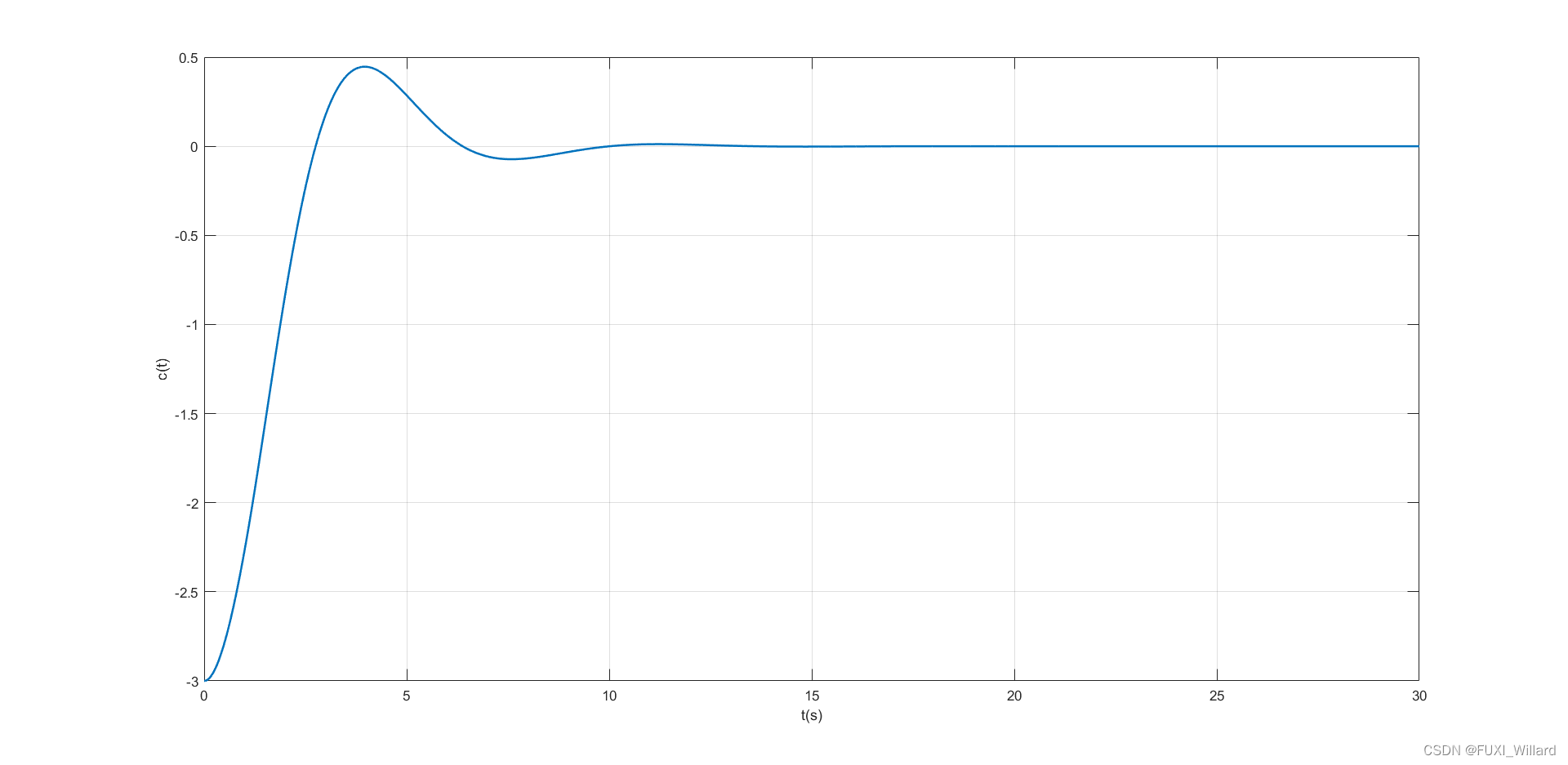
由上图可知,系统振荡收敛,系统的奇点为稳定焦点。
-
-
相关阅读:
ORM基本操作
cookie介绍:cookie实现增删改查功能
循环服务器
Redis——其他数据类型介绍
在javascript中重新加载/刷新页面的不同方法
基于spring boot的毕业设计论文选题申报管理系统
一个 不用充钱 也能让你变强的 VSCode 插件
mybatis-plugin插件执行原理
request爬虫入门
51单片机的基础知识汇总
- 原文地址:https://blog.csdn.net/qq_39032096/article/details/126909177