算法 - 计数排序（Counting_Sort）

目录

引言：

学习：

什么是计数排序（Counting_sort）？

定义：  

算法思想：

排序过程：

Step 1 ：

Step 2 ： 

Step 3 ： 

Step 4 :  

Step 5 ： 

依次进行填充的步骤： 

遍历临时数组空间并输出： 

实现： 

代码实现（C++）：

程序可以改进的几个点： 

改进后用代码实现（C）：

运行结果： 

总结：

参考资料：

---

引言：

今天在书上看到了计数排序，对计数排序的排序过程以及原理产生了兴趣并进行了学习最终用代码实现，计数排序属于8大主流排序中的一种，也是一种在不考虑空间的前提下快于任何排序算法的算法，这篇文章我将对计数排序的排序原理进行总结，在画板上对排序过程进行演示，并使用代码实现这个排序算法。

学习：

什么是计数排序（Counting_sort）？

在开始写计数排序的代码之前，我们先对计数排序的定义、算法思想、排序过程做一个简单的了解和梳理。

定义：  

计数排序（Counting_Sort）是一个非基于比较形式的排序算法，它也是一种以牺牲空间换取时间的过程。计数排序利用数组的有序性将元素依次存储进对应下标的数组空间中，然后再依次输出。

算法思想：

统计原来数组的数据，并将数据转换成下标存储到另外一个临时的空间里面，然后遍历临时空间把对应的下标值依次放回原数组，当遍历完临时空间并将对应的下标值全部依次放回原数组后就排好序了。

排序过程：

例如在这里我给出一组原始数据：

{1,3,2,5,5,6,9,8,2,4};

现在我们假设开辟的临时数组空间足够大的前提下，将数组空间画出来：

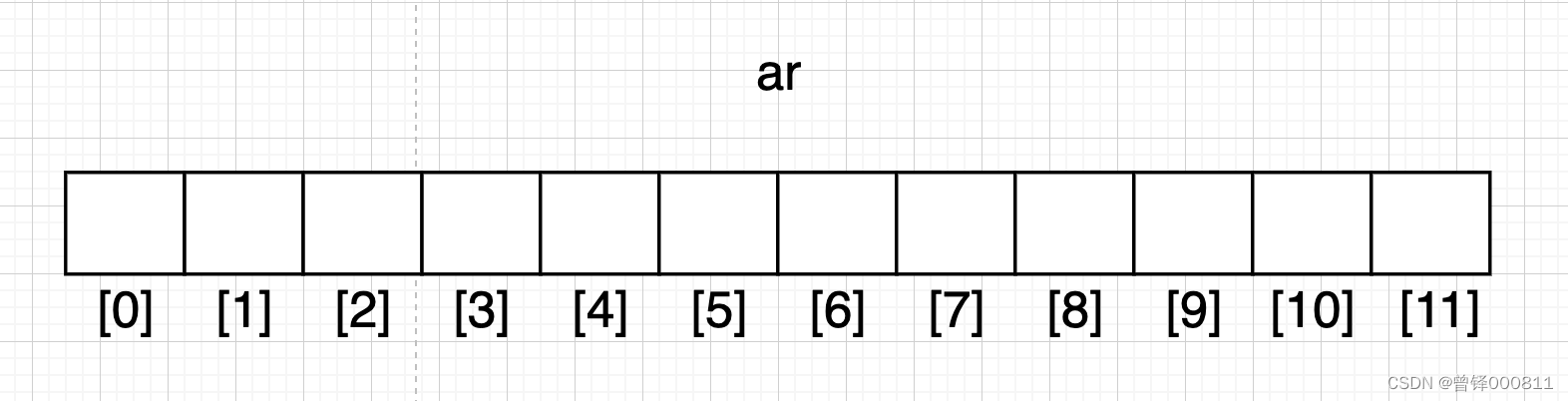
临时空间开辟完成后我们现在开始按照计数排序的规则对原始数据进行遍历并排序：

Step 1 ：

遍历至原始数据的第一个数据1时，将1存储至开辟的临沭数组空间中的1号下标位置，如图：

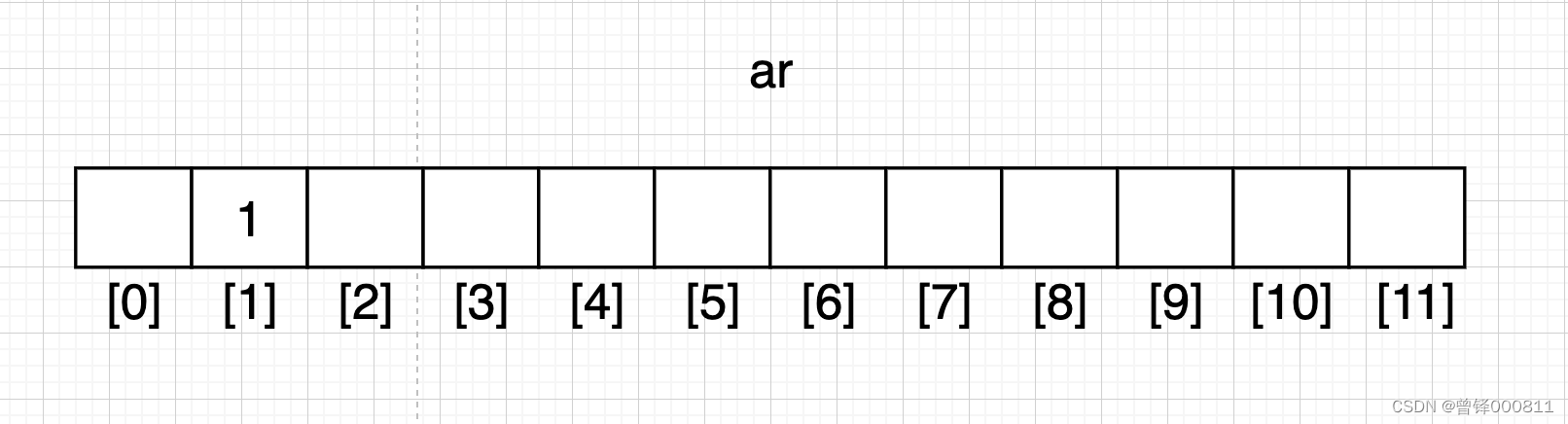
Step 2 ： 

遍历至第二个数据3时，我们再将3填充至对应的下标位置：

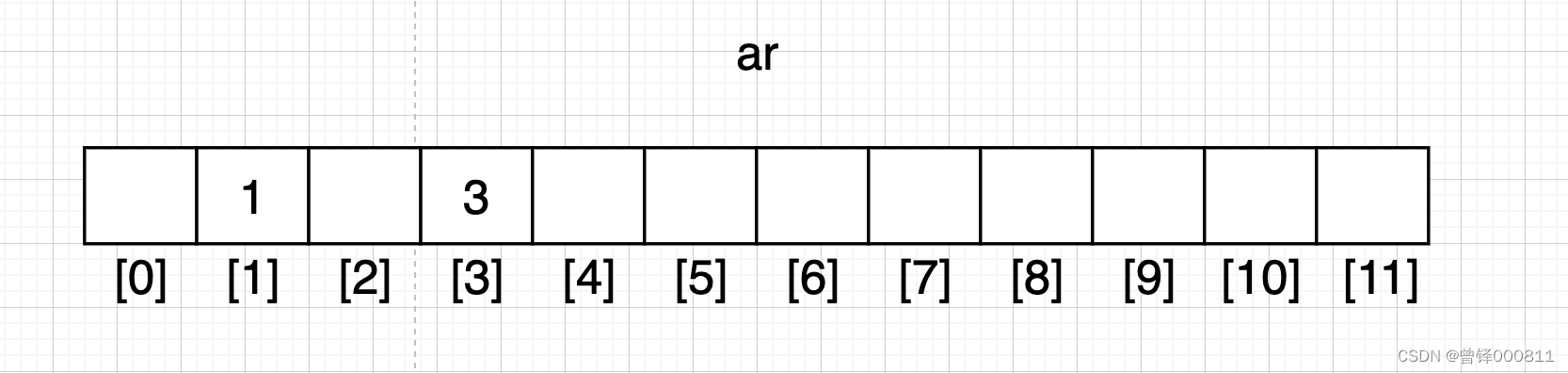
Step 3 ： 

遍历至第三个数据2时，将2填充至对应下标位置：

Step 4 :  

遍历至第四个数据5时，将5填充至对应下标位置：

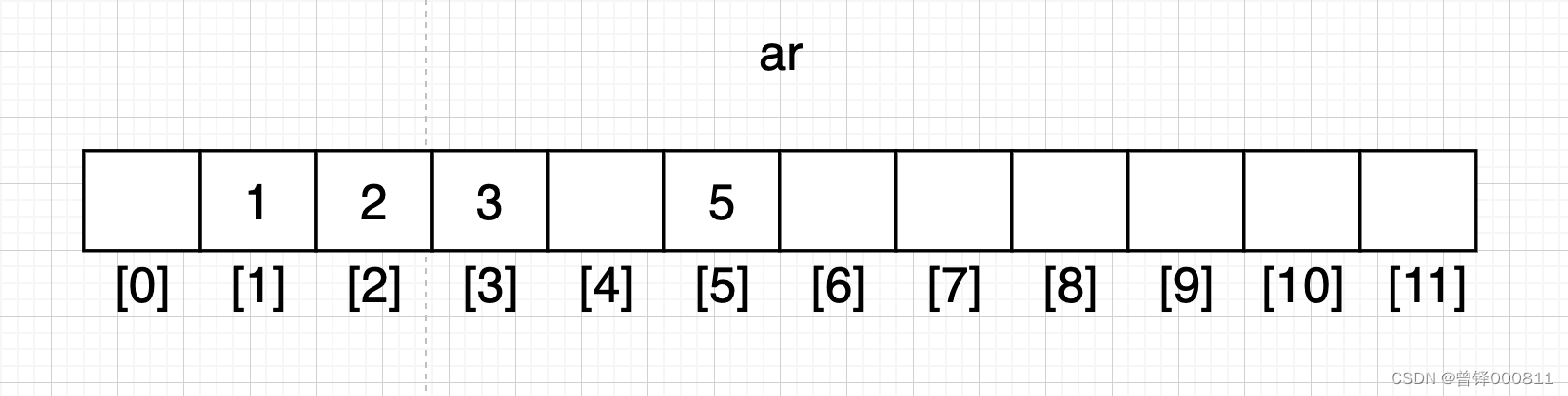
Step 5 ： 

遍历至第五个数据时，我们本来应该将5填充至 [5]号下标的位置，但此位置在之前已经被5填充过了，所以此时我们将5进行叠加，也就是说此时5号下标位置有两个数据5，一前一后：

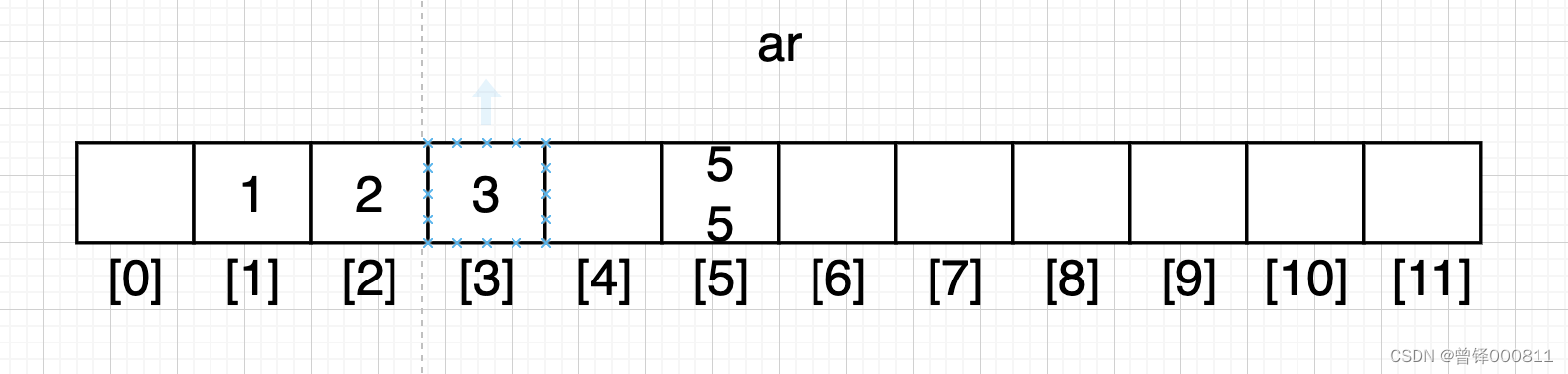
依次进行填充的步骤： 

按照上面的规律，我们将剩下的数据依次进行填充：

 

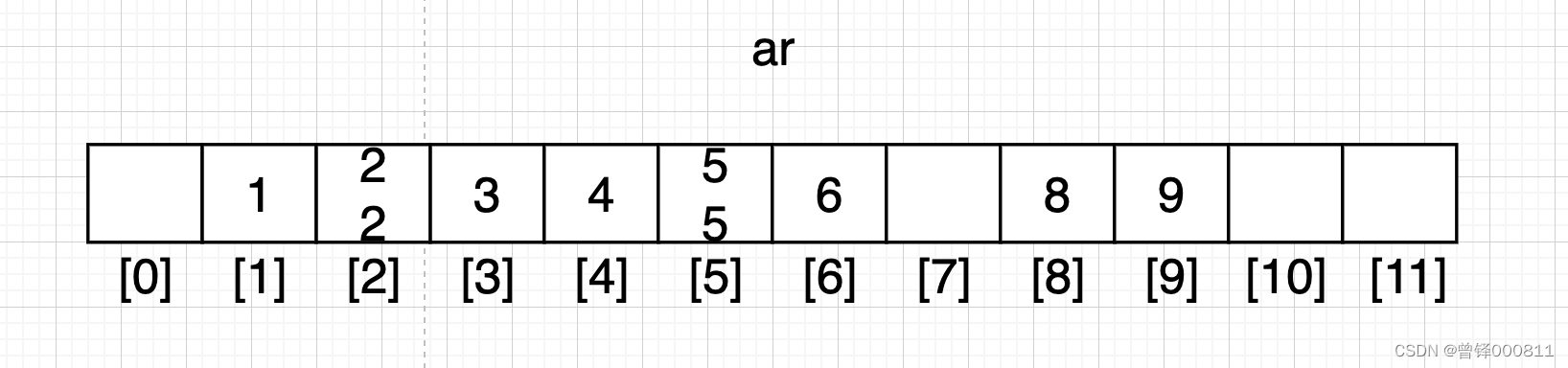
遍历临时数组空间并输出： 

此时填充完毕，将临时开放的数组空间进行遍历并输出，结果为：

1，2，2，3，4，5，5，6，8，9；

实现： 

代码实现（C++）：

#include
#include
#include
using namespace std;
int arr[11];//定义一个长度为11的数组
int main()
{
    int t = 0,n = 0;
    cin >> n;//输入要排序元素的个数
    for(int i = 1;i <= n;i++){//循环条件：当循环变量i小于元素个数
        cin >> t;//持续输入t
        arr[t]++;//将元素填充至arr数组中对应下标的位置
    }
    for(int i = 0;i <= n;i++){//循环条件：当循环变量i小于元素个数
        for(int j = 1;j <= arr[i];j++){//使用j下标对临时数组中每一个下标的空间进行遍历
            cout << i << " ";//输出元素
        }
    }
    return 0;
}

例如我在这里输入元素9个元素，运行结果为：

 

如图，成功的将输入的十个元素进行了升序排序：

程序可以改进的几个点： 

程序存在有这几个可以进行改进的地方：

1 ： 程序只能对个位数字进行排序，可以将程序改进，让程序可以排序个位数字、十位数字、甚至是百位数字；

3 ： 原程序是直接写在主程序中的，可以将排序封装为函数，在主程序中直接进行调用；

改进后用代码实现（C）：

#include
#include
#include
#include
#include
#define MAXSIZE 10
#define N 100
int temp[N];
void initar(int *ar,int len)//初始化ar，并将100以内的数组随机填充进ar数组中
{
	assert(ar != nullptr);
	for(int i = 0;i < len;i++){
		ar[i] = rand() % 100；
	}
}
void showar(int *ar,int len)//打印数组函数
{
	assert(ar != nullptr);
	for(int i = 0;i < len;i++){
		printf("%d ",ar[i]);
	}
	printf("\n--------------------------\n");
}
void Counting_Sort(int *ar,int len)//计数排序函数
{
	assert(ar != nullptr);
	for(int i = 0;i < len;i++)//将数据依次填充进临时空间temp中对应的下标位置
		temp[ar[i]]++;//按照元素编号依次填写进temp临时空间中
	for(int i = 0,j = 0;i < N;i++){//遍历临时数组空间中的元素并将其放入至ar数组中进行输出
		while(temp[i]--)//放一个减一个
			ar[j++] = i;
	}
}
int main()
{
    srand((unsigned int)time(NULL));
	int ar[MAXSIZE];
	initar(ar,MAXSIZE);
	printf("原始数据为：\n");
	showar(ar,MAXSIZE);
    printf("\n经过计数排序后的数据为：\n");
	Counting_Sort(ar,MAXSIZE);
	showar(ar,MAXSIZE);
    return 0;
}

运行结果： 

总结：

计数排序（Counting_Sort）是一种非基于比较形式的算法，在之前所实现过的冒泡排序、选择排序、插入排序等排序算法都是基于比较的算法，而计数排序则是利用了数组天然的有序性对数据进行归类划分，然后再对临时数组空间进行遍历并输出。

设输入的线性表长度为n，则计数排序的时间复杂度为O（n），这无异是快于前面所学习到的任何算法的，且时间复杂度极低，但这一切的条件都是以空间作为代价的。

计数排序对输入的数据有附加的限制条件：

1、输入的线性表的元素属于有限偏序集S；

2、设输入的线性表的长度为n，|S|=k（表示集合S中元素的总数目为k），则k=O(n)。

在这两个条件下，计数排序的复杂性为O(n)。

参考资料：

计数排序_百度百科

Cukor丘克 - 十大经典排序算法（C语言描述）