傅立叶及其python应用

前言

1. 本文是傅立叶及其python应用系列的第三篇文章
2. 对应的仓库地址为https://github.com/yuanzhoulvpi2017/tiny_python/tree/main/Fourier_Series

介绍

第二篇主要介绍了傅立叶的核心：“傅里叶级数就是函数在某个函数空间中各个基底的投影和“，然后基于这个核心，我们做了一个数值模拟：如何去拟合一个任意函数。

但是在实际应用的时候，我们并不会去直接的按照原理，写代码去实现。而是直接调用非常稳定的、安全的api，帮助我们解决问题。

在这次第三篇中，将给你展示一个非常神奇的傅立叶应用。而这个应用，也会帮助你进一步了解傅立叶的核心。

那我们直接开始吧。

api介绍

如果你对科学计算感兴趣，你在numpy、scipy、pytorch、tensorflow包里面会发现一个叫fft模块。

而fft全称为Fast Fourier Transform ，中文翻译的也很直接，就叫快速傅里叶变换。

1. numpy: https://numpy.org/doc/stable/reference/generated/numpy.fft.fft.html
2. scipy：https://docs.scipy.org/doc/scipy/reference/generated/scipy.fft.fft.html#scipy.fft.fft
3. pytorch:https://pytorch.org/docs/stable/fft.html
4. tensorflow: https://www.tensorflow.org/api_docs/python/tf/signal/fft

虽然属于不同的包，但是本质上都差不多，对数据做快速傅立叶变换。从离散数据中提取出信息。

那么到底怎么处理离散的数据，能提取出什么信息？其实这些包的文档里面都没说。那么我接下来将要分享一个案例，带大家打开傅立叶应用的大门。

案例 - 使用傅里叶变换求噪声中隐藏的信号的频率分量

导入包

就暂时使用scipy的fft模块来做演示。

import numpy as np
from scipy.fft import fft
import matplotlib.pyplot as plt
1
2
3

创建一个样本数据

1. 指定信号的参数，采样频率为 1 kHz，信号持续时间为 1.5 秒。

Fs = 1000  #Sampling frequency
T = 1 / Fs  #Sampling period
L = 1500;  #Length of signal
t = np.arange(L) * T  #Time vector
1
2
3
4

2. 构造一个信号，其中包含幅值为 0.7 的 50 Hz 正弦、幅值为 1 的 120 Hz 正弦量、幅值为 0.2 的 10 Hz 正弦量（简单的来说就是三个sin函数相加）。
3. 再添加一点随机值到里面。

S = 0.7 * np.sin(2 * np.pi * 50 * t) + np.sin(2 * np.pi * 120 * t) + 0.2 * np.sin(2 * np.pi * 10 * t)
X = S + 2 * np.random.rand(S.shape[0])
1
2

4. 数据可视化，大概看看数据的前100是啥样子的。

fig, ax = plt.subplots(figsize=(10, 5), dpi=120)
ax.plot(1000 * t[:100], X[:100])
ax.set_title("Signal Corrupted with Zero-Mean Random Noise")
ax.set_xlabel("t (milliseconds)")
ax.set_ylabel("X(t)")
1
2
3
4
5

可以看出来，下面什么信息都看不到，杂乱无章的数据而已。

5. 计算数据的傅立叶变换
6. 计算双侧频谱 P2。然后基于 P2 和偶数信号长度 L 计算单侧频谱 P1。

Y = fft(X)
P2 = np.abs(Y / L)
P1 = P2[1:np.int32(L / 2 + 1)]
P1[1:] = 2 * P1[1:]
1
2
3
4

7. 对P1数据可视化看一下：

f = Fs * np.arange(L / 2) / L
fig, ax = plt.subplots(figsize=(10, 5), dpi=120)
ax.plot(f, P1)
ax.set_title('Single-Sided Amplitude Spectrum of X(t)')
ax.set_xlabel('f (Hz)')
ax.set_ylabel('|P1(f)|')
# ax.set_xlim([0, 150])
1
2
3
4
5
6
7

这个图看起来，好像有3个高峰，然后好像有很多噪声。那么我们重点放在三个峰那里，看看能不能从三个峰那里发现有用的信息。

8. 更新可视化

f = Fs * np.arange(L / 2) / L
fig, ax = plt.subplots(figsize=(10, 5), dpi=120)
ax.plot(f, P1)
ax.set_title('Single-Sided Amplitude Spectrum of X(t)')
ax.set_xlabel('f (Hz)')
ax.set_ylabel('|P1(f)|')
ax.set_xlim([0, 150])
for temp_y in [0.2, 0.7, 1.0]:
    ax.hlines(temp_y, xmin=0, xmax=150, colors='gray', linestyles='-.')

for temp_x in [10, 50, 120]:
    ax.vlines(x=temp_x, ymin=0, ymax=1,colors='red', linestyles='-.' )
1
2
3
4
5
6
7
8
9
10
11
12

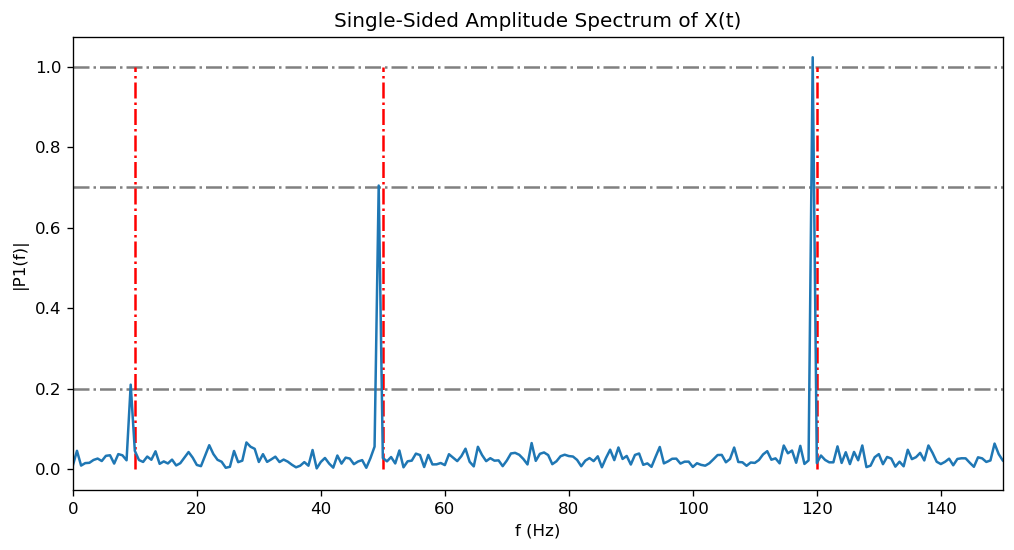
从上面图可以看到：

1. 三个峰的x轴的位置都是在10，50，120附近。
2. 三个峰的y轴的位置都是在0.2，0.7，1.0附近。

这三个数值到底是什么意思？

其实你只要把文章翻到最前面就可以看到了。在文字最前面的构建样本数据的时候，写了这样的话：“其中包含幅值为 0.7 的 50 Hz 正弦、幅值为 1 的 120 Hz 正弦量、幅值为 0.2 的 10 Hz 正弦量”

可以得出来了：x轴的位置对应的是频率部分，y轴对应的是震幅部分。

是不是破案了！！
我们通过傅立叶变换，然后对数据简单做了计算，竟然能求出来原始数据的参数！！！

在最后，牢记这句话：傅里叶级数就是函数在某个函数空间中各个基底的投影和

end

那么这就是本期的全部内容，如果想看更多，点击下方的代码链接和文章list，下期再见！

代码

傅立叶及其python应用所有的代码和数据全部都免费共享！

1. 代码所在文件夹为：https://github.com/yuanzhoulvpi2017/tiny_python/tree/main/Fourier_Series
2. 代码文件为03开头的ipynb格式文件

参考链接

1. 主要参考了Matlab文档，翻译成python版本的代码 https://ww2.mathworks.cn/help/matlab/ref/fft.html
2. https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.find_peaks_cwt.html

本系列文章

list

相关文章

list