【编译原理】-- 第二章（二）（短语、简单短语、句柄、文法二义性、语法树、例题）

目录

一、句型的分析

1、规范推导和规范归约

2、短语、简单短语和句柄

3、语法树

4、通过树来寻找短语、简单短语、句柄

二、文法的二义性

1、文法二义性的定义

2、文法二义性的消除

（1）定义规定或规则

（2）改写文法

三、例题

1、语言L={ambn ,m>=1,n>=1},试写出文法。

2、语言L={anbncm ,m>=1,n>=1},试写出文法。

3、语言L={anbbn ,n>=1},试写出文法。

4、语言L={anbmcmdn ,m>=1,n>=1},试写出文法。

5、语言L={ambn ,n>=m>=1},试写出文法。

 

---

一、句型的分析

1、规范推导和规范归约

最左（右）推导：在任一步推导v=>w中，都是对符号串v的最左(右）非终结符号进行替换,称最左（右）推导。

规范推导：即最右推导。

规范句型：由规范推导所得的句型。

规范归约：规范推导的逆过程，称规范归约或最左归约。

例:

G[<标识符>]
<标识符>→<字母>|<标识符><字母>
|<标识符><数字>
<字母>→a|b|...|z|A|...|Z
<数字>→0|1|2|...|9

规范推导
<标识符>
=><标识符> <字母>
=><标识符>y
=><标识符> <数字>y
=><标识符>4y
=><字母>4y
=>a4y

规范归约
a4y
<≠<字母>4y
<≠ <标识符>4y
<≠ <标识符><数字>y
<≠<标识符>y
<≠ <标识符><字母>
<≠ <标识符>

2、短语、简单短语和句柄

短语：文法G[Z], ω=xuy是一句型,x,y∈V*，如有 Z=*>xUy,且U=+>u, U∈Vn, u ∈V+，称u是一个相对于非终结符号U句型ω的短语。

简单短语：文法G[Z], ω=xuy是一句型，如有 Z=*>xUy,且U=>u, U∈Vn, u ∈V+，称u是一个相对于非终结符号U句型ω的简单短语。

句柄：句型最左边的简单短语为该句型的句柄，一个句型只有一个句柄。

说明：

• 短语和简单短语必须是针对某一句型来说的，并且是该句型的一个字串。
• 短语和简单短语必须是相对某一非终结符号的。
• 两个条件缺一不可。
• 一个句型可以有几个短语和简单短语。
• 一个当前句型只有一个句柄（无二义性的文法）
• 最左归约归约的当前句型的句柄。

例：

G[S]：
S→AB
A→Aa|bB
B→a|Sb

问题:给出句型baSb的短语、简单短语和句柄。

(1) S=>AB=>bBB =>baB=>baSb           且B=>Sb
(2) S=>AB =>ASb =>bBSb=>baSb        且B=>a
(3) S=>AB =+>baSb                               且A=+>ba

Sb是相对于B、句型baSb的短语且为简单短语，
a是相对于B、句型baSb的短语且为简单短语，
ba是相对A、句型baSb的短语 句柄为a。

3、语法树

语法树：一个句型或句子推导过程的图示法表示，形成一棵语法树。

根：开始符号。

子树：某一非终结符号 (子树的根)及其下面的分支。

叶：树的末端结点。

语法树的全部末端结点（自左向右）形成当前句型。

例:

G[S]：
S→AB
A→Aa|bB
B→a|Sb

最左推导        
S=>AB
=>bBB
=>baB
=>baSb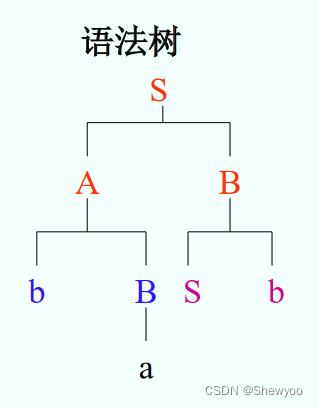

 

说明：

设文法G=(Vn,Vt,P,S),对G的任何句型都能构造与之关联的、满足下列条件的一课语法树。

• 每个结点都有一个标记，此标记是V=Vn∪Vt∪ε中的一个符号。
• 树根的标记是文法的开始符号S。
• 若某一结点至少有一个分支结点，则该结点上的标记一定是非终结符号。
• 若A的结点有k个分支结点，其分支结点的标记分别为A1,A2,...,Ak,则A→A1A2...Ak一定是G的一条规则。

4、通过树来寻找短语、简单短语、句柄

短语：子树的末端结点形成的符号串。

简单子树：只有一层分支的子树。

简单短语：简单子树的末端结点形成的符号串。

例：

          句型baSb的语法树

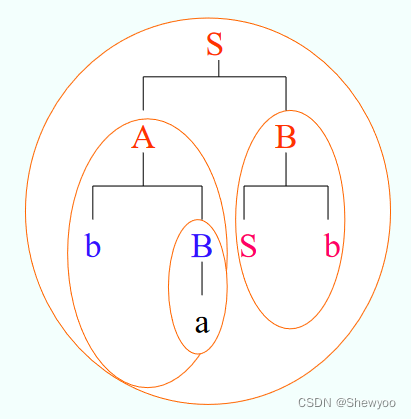
共有三颗子树，

三个短语:ba ,a, Sb，baSb
简单短语: a, Sb
句柄: a

 1、如何找短语？

从树根S开始，找S的末端结点是：baSb（也就是句型本身）

然后往下找A的末端结点是：ba

                  B的末端结点是：Sb

再往下只有B有末端结点是：a

2、如何找简单短语？

先找到简单子树即只有一层分支的子树；

然后简单子树的末端结点形成的符号串即简单短语。

3、如何找句柄？

找左边的简单短语

结论：

• 对于某个句型，每个推导,都有一个相应的语法树；但不同的推导也可能有相同的语法树。
• 树的末端结点形成所要推导的句型。
• 但某个句型也可能对应两棵不同的语法树，这就是文法的二义性问题

二、文法的二义性

1、文法二义性的定义

• 如果文法G的某一个句子存在两棵或两棵以上不同的语法树，则称句子是二义性的。
• 如果一文法含有二义性的句子，则称该文法是二义性的，否则该文法是无二义性的。

 说明：

• 文法的二义性：某一句子有两个不同的最左（右）推导，或两个不同的最左（规范）归约。
• 文法的二义性是不可判定的：不存在一种算法。
• 证明文法的二义性只能试图找到某句子，该句子存在两颗不同的语法树或两个不同的最左（右）推导。
• 特例：若一文法G既含左递归又含右递归，则G必是二义性文法.(是经验)

例:

证明文法G[S]：S→aSb|Sb|b为二义性文法。

证明：对于句子abbb存在两个不同的最左推导
最左推导1： S=>aSb=>aSbb=>abbb
最左推导2： S=>Sb=>aSbb=>abbb
因此，句子abbb是二义性的，由于文法存在二义性的句子，所以文法G[S]是二义性的。

2、文法二义性的消除

（1）定义规定或规则

例：

G1[E]:E→E+E|E*E|(E)|i

规定：四则运算法则，成无二义性文法。

G[S]: S →if B then S else S|if B then S

规定：else跟与它最近尚未匹配的then匹配，成无二义性文法

（2）改写文法

例：

G1[E]:E→E+E|E*E|(E)|i

二义性文法，无优先关系信息，不能直接使用。

G2[E]:
E→E+T|T
T→T*F|F
F→(E)|i

无二义性文法，含四则运算信息，语法分析时使用。

三、例题

1、语言L={ambn ,m>=1,n>=1},试写出文法。

G[S]：
S→AB
A→Aa|a
B→bB|b
或G[S]：
S→AB
A→aA|a
B→bB|b

2、语言L={anbncm ,m>=1,n>=1},试写出文法。

G[S]：
S→AB
A→aAb|ab
B→cB|c

3、语言L={anbbn ,n>=1},试写出文法。

G[S]：
S→aAb
A→aAb|b

或G[S]：
S→aSb|A
A→abb

4、语言L={anbmcmdn ,m>=1,n>=1},试写出文法。

G[S]：
S→aSd|aAd
A→bAc|bc

5、语言L={ambn ,n>=m>=1},试写出文法。

解： 改写为等价语言 L={ambmbk ,m>=1,k>=0}

G1[S]:S→AB
A→aAb|ab
B→bB|ε

G2[S]:
S→aAb
A→aAb|Ab|ε

或改写为等价语言 L={ambkbm ,m>=1,k>=0}

G3[S]:
S→aSb|aAb
A→bA|ε

---