布隆过滤器的原理

引言

布隆过滤器用于redis中拦截缓存和数据库中都没有的数据。避免缓存穿透。

简介

简单来说，布隆过滤器是一种数据结构。特点是存在性检测，如果布隆过滤器中不存在，那么实际数据库中不存在。如果布隆过滤器中存在，实际数据不一定存在。相比与传统数据结构，它更高效。占用的空间更少，缺点是他对存在的判断具有概率性。

实现原理

在谈到原理时之前，我们来看看布隆过滤器的数据结构，它是一个bit数组。更具几个hash算法计算数组下标值。当有数据查询时，在布隆过滤器中通过jhash值计算数组下标，如果所有下标的数组上的值为1标识，缓存中可能存在数据。如果有一个不为1，缓存中没有这个数据。

具体流程如下

 

为什么说，如果布隆过滤器中存在，实际数据不一定存在呢？

因为布隆过滤器的长度和hash算法的个数有关。如果一个新数据在经过hash计算后得到的位置都为1，可能是别的数据设置的1。一个新数据的所有位置可能都被其他数据设值。所以布隆过滤器中标识存在，不一定存在。

接着上面的话题继续说，很显然，长度过小的布隆过滤器很快所有的bit位都被置为1了，查询任意值都会返回“可能存在”的，这样就起不到过滤的目的。说明，布隆过滤器的长度越小，其误报率就越高，布隆过滤器的长度越长，误报率越低。

接下来再看看哈希函数的个数是否对误报率有影响。如果哈希函数的个数越多，那么bit位会迅速填满，也就是布隆过滤器bit位置为1的速度会加快，且布隆过滤器的效率越低。换句话说，如果哈希函数的个数越多，布隆过滤器bit位置为1的速度就越快，且效率就会越低；如果哈希函数个数越少，bit位置为1的速度就越慢，但是误报率就越高了。很显然，布隆过滤器的长度，哈希函数的个数，误报率以及插入元素的个数4者之间存在着某种关系，可能是线性关系。到底存在怎么样的关系呢？直接上公式：

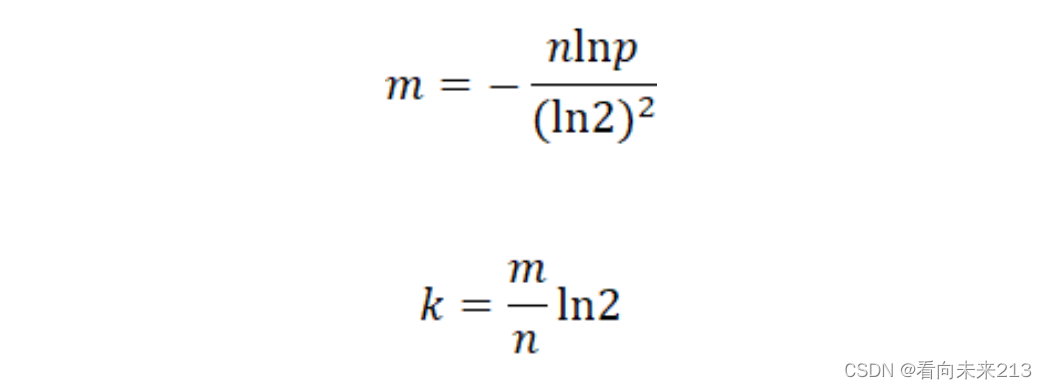
上面两个公式中，斜体字母m,n,p,k分别代表，m为布隆过滤器长度，n为插入的元素个数，k为哈希函数个数，p为误报率。这样，有了上面两个公式就可以方便选择哈希函数的个数和布隆过滤器的长度了。至于如何推导这两个公式，我将会在后续文章中写到，欢迎继续关注。 

布隆过滤器为什么可以防止缓冲穿透

布隆过滤器虽然对存在数据的过滤具有误报率的缺点，但是对数据做不存在的过滤是100%准确的。所以布隆过滤器可以防止缓存穿透。而且前面简介中提到了它的优点是高效，占用空间更少。尤其针对上亿级数据，在高并发场景下，它的性能更优。

布隆过滤器的缺点

但是布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。

　　另外，一般情况下不能从布隆过滤器中删除元素。我们很容易想到把位列阵变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。

布隆过滤器原理 - jessee-blog - 博客园布隆过滤器的原理_快马扬鞭的博客-CSDN博客_布隆过滤器原理