• 【监督学习】套索回归与岭回归（含代码）

    🔎大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流🔎

    📝个人主页－Sonhhxg_柒的博客_CSDN博客 📃

    🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​

    📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

    ​

     🖍foreword

    ✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

    如果你对这个系列感兴趣的话，可以关注订阅哟👋

    1、正则化

    L1正则化

    L1正则化的式子是这样的，原损失函数加上一个一阶范数： 

     

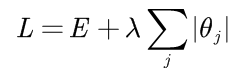
    这样根据上面L2正则化的推导思路就可以得到这样的一张图

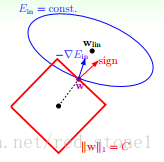
    这里写图片描述

    L2正则化

    L2正则化就是在原来的损失函数的基础上加上权重的平方和：

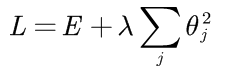
    接下来解释为什么要这样做，正则化的目的是约束权重不能过多或过大，这样会使模型变的复杂，从而有可能导致过拟合。因此我们就在末尾加上了一个只与权重有关的多项式，这样再优化损失函数时，要原来的损失函数和权重都最小，相当于在最小化损失函数的同时加了一个条件，在满足这个条件下，对损失函数进行优化。 

    为什么要加平方和，而不是绝对值的和或者说三次方、四次方、n次方和？

     

    L1，L2正则的区别与作用
    L2正则化和L1正则化都可以减少过拟合，而L2正则化更多的作用是使参数大小更加均衡，防止出现某一个特征权重过大的情况，也就是说防止某个特征的权重过大、模型对某个特征过分敏感，这样即使数据集中有噪声，模型也不会对噪声特别敏感而发生过拟合。

    L1正则化则可以使一些权重等于0，从而实现自动选择特征的效果，从而化简模型，防止模型过于复杂而过拟合。

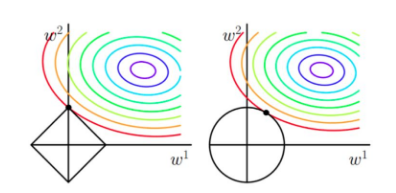
    为什么L1可以使部分权重等于0，而L2不可以呢？

    看这两张图就可以理解了，L1正则化在优化的时候很容易取到角点，使一部分权重为0，从而实现自动选择特征，L2正则化中，正则项表示出来的图像是光滑的圆形，所以很难取到坐标轴上的点，很使部分特征权重为0。

     

     2、岭回归

    岭回归(英文名：ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

    1. 为什么损失精度和无偏性？

    根据前面我介绍的无偏估计的概念，普通的线性回归是一种无偏估计，也就是这种估计的期望值是十分近似于总体数据的真实期望值的，而在这种估计方法之上加一个正则项，势必会改变估计的期望值，因此这种估计就变成了有偏估计。正则化的作用是防止过拟合（可以看这篇），相当于对目标函数的优化加上了一个约束条件，因此这样的优化效果一定会小于等于不加正则项的优惠效果，因此会损失精度。

    2. 为什么对病态数据的拟合比普通的线性回归要强？

    我对病态数据的理解就是，噪声过大、数据分布左偏或有偏、有较多离群值等等，这样的数据用普通的线性回归学习在学习样本的特征时也会过多的学习数据的噪声特征和离群特征，这样会导致模型过拟合，使模型的泛化能力（就是模型推广到不同数据集的表现）变差，因此可以加一些“约束”，也就是正则项，主动放弃一些模型在训练集上的精度，而使模型的泛化能力提升。

     通线性回归的目标函数（看这里）是：

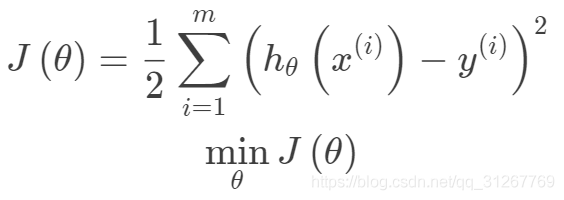
    岭回归的目标函数是：

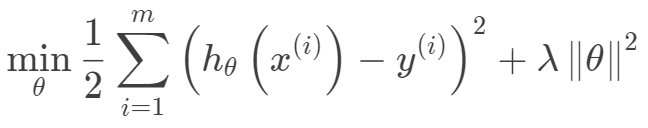
    另外从最小二乘的角度来看，通过引入二范正则项，使得 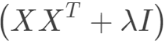    满秩，强制矩阵可逆。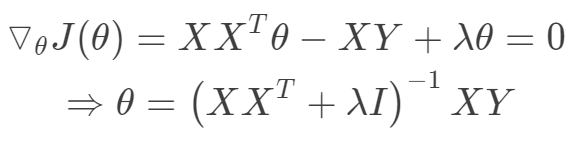

     单位矩阵I的主对角线为1，像山岭一样，这就是岭回归的由来。

    3、LASSO回归
     

    Lasso回归和岭回归十分相似，不过是采用一范数来约束，就是加上了一个L1正则项。

    Lasso回归的目标函数是：

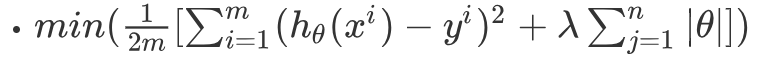
    求导之后是MSE加上一个符号函数。

    总结：岭回归很难剔除变量，而LASSO回归模型，将惩罚项由L2范数变为L1范数，可以将一些不重要的回归系数缩减为0，达到剔除变量的目的。
     

    4、代码实现

    岭回归代码（从零实现）

    1. from __future__ import print_function, division
    2. import numpy as npnp
    3. import math
    4. from mlfromscratch.utils import normalize, polynomial_features
    5.  
    6. class l1_regularization():
    7.     """ Regularization for Lasso Regression """
    8.     def __init__(self, alpha):
    9.         self.alpha = alpha
    10.     
    11.     def __call__(self, w):
    12.         return self.alpha * np.linalg.norm(w)
    13.  
    14.     def grad(self, w):
    15.         return self.alpha * np.sign(w)
    16.  
    17. class l2_regularization():
    18.     """ Regularization for Ridge Regression """
    19.     def __init__(self, alpha):
    20.         self.alpha = alpha
    21.     
    22.     def __call__(self, w):
    23.         return self.alpha * 0.5 *  w.T.dot(w)
    24.  
    25.     def grad(self, w):
    26.         return self.alpha * w
    27.  
    28. class l1_l2_regularization():
    29.     """ Regularization for Elastic Net Regression """
    30.     def __init__(self, alpha, l1_ratio=0.5):
    31.         self.alpha = alpha
    32.         self.l1_ratio = l1_ratio
    33.  
    34.     def __call__(self, w):
    35.         l1_contr = self.l1_ratio * np.linalg.norm(w)
    36.         l2_contr = (1 - self.l1_ratio) * 0.5 * w.T.dot(w) 
    37.         return self.alpha * (l1_contr + l2_contr)
    38.  
    39.     def grad(self, w):
    40.         l1_contr = self.l1_ratio * np.sign(w)
    41.         l2_contr = (1 - self.l1_ratio) * w
    42.         return self.alpha * (l1_contr + l2_contr) 
    43.  
    44. class Regression(object):
    45.     """ Base regression model. Models the relationship between a scalar dependent variable y and the independent 
    46.     variables X. 
    47.     Parameters:
    48.     -----------
    49.     n_iterations: float
    50.         The number of training iterations the algorithm will tune the weights for.
    51.     learning_rate: float
    52.         The step length that will be used when updating the weights.
    53.     """
    54.     def __init__(self, n_iterations, learning_rate):
    55.         self.n_iterations = n_iterations
    56.         self.learning_rate = learning_rate
    57.  
    58.     def initialize_weights(self, n_features):
    59.         """ Initialize weights randomly [-1/N, 1/N] """
    60.         limit = 1 / math.sqrt(n_features)
    61.         self.w = np.random.uniform(-limit, limit, (n_features, ))
    62.  
    63.     def fit(self, X, y):
    64.         # Insert constant ones for bias weights
    65.         X = np.insert(X, 0, 1, axis=1)
    66.         self.training_errors = []
    67.         self.initialize_weights(n_features=X.shape[1])
    68.  
    69.         # Do gradient descent for n_iterations
    70.         for i in range(self.n_iterations):
    71.             y_pred = X.dot(self.w)
    72.             # Calculate l2 loss
    73.             mse = np.mean(0.5 * (y - y_pred)**2 + self.regularization(self.w))
    74.             self.training_errors.append(mse)
    75.             # Gradient of l2 loss w.r.t w
    76.             grad_w = -(y - y_pred).dot(X) + self.regularization.grad(self.w)
    77.             # Update the weights
    78.             self.w -= self.learning_rate * grad_w
    79.  
    80.     def predict(self, X):
    81.         # Insert constant ones for bias weights
    82.         X = np.insert(X, 0, 1, axis=1)
    83.         y_pred = X.dot(self.w)
    84.         return y_pred
    85.  
    86. class LinearRegression(Regression):
    87.     """Linear model.
    88.     Parameters:
    89.     -----------
    90.     n_iterations: float
    91.         The number of training iterations the algorithm will tune the weights for.
    92.     learning_rate: float
    93.         The step length that will be used when updating the weights.
    94.     gradient_descent: boolean
    95.         True or false depending if gradient descent should be used when training. If 
    96.         false then we use batch optimization by least squares.
    97.     """
    98.     def __init__(self, n_iterations=100, learning_rate=0.001, gradient_descent=True):
    99.         self.gradient_descent = gradient_descent
    100.         # No regularization
    101.         self.regularization = lambda x: 0
    102.         self.regularization.grad = lambda x: 0
    103.         super(LinearRegression, self).__init__(n_iterations=n_iterations,
    104.                                             learning_rate=learning_rate)
    105.     def fit(self, X, y):
    106.         # If not gradient descent => Least squares approximation of w
    107.         if not self.gradient_descent:
    108.             # Insert constant ones for bias weights
    109.             X = np.insert(X, 0, 1, axis=1)
    110.             # Calculate weights by least squares (using Moore-Penrose pseudoinverse)
    111.             U, S, V = np.linalg.svd(X.T.dot(X))
    112.             S = np.diag(S)
    113.             X_sq_reg_inv = V.dot(np.linalg.pinv(S)).dot(U.T)
    114.             self.w = X_sq_reg_inv.dot(X.T).dot(y)
    115.         else:
    116.             super(LinearRegression, self).fit(X, y)
    117.  
    118. class LassoRegression(Regression):
    119.     """Linear regression model with a regularization factor which does both variable selection 
    120.     and regularization. Model that tries to balance the fit of the model with respect to the training 
    121.     data and the complexity of the model. A large regularization factor with decreases the variance of 
    122.     the model and do para.
    123.     Parameters:
    124.     -----------
    125.     degree: int
    126.         The degree of the polynomial that the independent variable X will be transformed to.
    127.     reg_factor: float
    128.         The factor that will determine the amount of regularization and feature
    129.         shrinkage. 
    130.     n_iterations: float
    131.         The number of training iterations the algorithm will tune the weights for.
    132.     learning_rate: float
    133.         The step length that will be used when updating the weights.
    134.     """
    135.     def __init__(self, degree, reg_factor, n_iterations=3000, learning_rate=0.01):
    136.         self.degree = degree
    137.         self.regularization = l1_regularization(alpha=reg_factor)
    138.         super(LassoRegression, self).__init__(n_iterations, 
    139.                                             learning_rate)
    140.  
    141.     def fit(self, X, y):
    142.         X = normalize(polynomial_features(X, degree=self.degree))
    143.         super(LassoRegression, self).fit(X, y)
    144.  
    145.     def predict(self, X):
    146.         X = normalize(polynomial_features(X, degree=self.degree))
    147.         return super(LassoRegression, self).predict(X)
    148.  
    149. class PolynomialRegression(Regression):
    150.     """Performs a non-linear transformation of the data before fitting the model
    151.     and doing predictions which allows for doing non-linear regression.
    152.     Parameters:
    153.     -----------
    154.     degree: int
    155.         The degree of the polynomial that the independent variable X will be transformed to.
    156.     n_iterations: float
    157.         The number of training iterations the algorithm will tune the weights for.
    158.     learning_rate: float
    159.         The step length that will be used when updating the weights.
    160.     """
    161.     def __init__(self, degree, n_iterations=3000, learning_rate=0.001):
    162.         self.degree = degree
    163.         # No regularization
    164.         self.regularization = lambda x: 0
    165.         self.regularization.grad = lambda x: 0
    166.         super(PolynomialRegression, self).__init__(n_iterations=n_iterations,
    167.                                                 learning_rate=learning_rate)
    168.  
    169.     def fit(self, X, y):
    170.         X = polynomial_features(X, degree=self.degree)
    171.         super(PolynomialRegression, self).fit(X, y)
    172.  
    173.     def predict(self, X):
    174.         X = polynomial_features(X, degree=self.degree)
    175.         return super(PolynomialRegression, self).predict(X)
    176.  
    177. class RidgeRegression(Regression):
    178.     """Also referred to as Tikhonov regularization. Linear regression model with a regularization factor.
    179.     Model that tries to balance the fit of the model with respect to the training data and the complexity
    180.     of the model. A large regularization factor with decreases the variance of the model.
    181.     Parameters:
    182.     -----------
    183.     reg_factor: float
    184.         The factor that will determine the amount of regularization and feature
    185.         shrinkage. 
    186.     n_iterations: float
    187.         The number of training iterations the algorithm will tune the weights for.
    188.     learning_rate: float
    189.         The step length that will be used when updating the weights.
    190.     """
    191.     def __init__(self, reg_factor, n_iterations=1000, learning_rate=0.001):
    192.         self.regularization = l2_regularization(alpha=reg_factor)
    193.         super(RidgeRegression, self).__init__(n_iterations, 
    194.                                             learning_rate)
    195.  
    196. class PolynomialRidgeRegression(Regression):
    197.     """Similar to regular ridge regression except that the data is transformed to allow
    198.     for polynomial regression.
    199.     Parameters:
    200.     -----------
    201.     degree: int
    202.         The degree of the polynomial that the independent variable X will be transformed to.
    203.     reg_factor: float
    204.         The factor that will determine the amount of regularization and feature
    205.         shrinkage. 
    206.     n_iterations: float
    207.         The number of training iterations the algorithm will tune the weights for.
    208.     learning_rate: float
    209.         The step length that will be used when updating the weights.
    210.     """
    211.     def __init__(self, degree, reg_factor, n_iterations=3000, learning_rate=0.01, gradient_descent=True):
    212.         self.degree = degree
    213.         self.regularization = l2_regularization(alpha=reg_factor)
    214.         super(PolynomialRidgeRegression, self).__init__(n_iterations, 
    215.                                                         learning_rate)
    216.  
    217.     def fit(self, X, y):
    218.         X = normalize(polynomial_features(X, degree=self.degree))
    219.         super(PolynomialRidgeRegression, self).fit(X, y)
    220.  
    221.     def predict(self, X):
    222.         X = normalize(polynomial_features(X, degree=self.degree))
    223.         return super(PolynomialRidgeRegression, self).predict(X)
    224.  
    225. class ElasticNet(Regression):
    226.     """ Regression where a combination of l1 and l2 regularization are used. The
    227.     ratio of their contributions are set with the 'l1_ratio' parameter.
    228.     Parameters:
    229.     -----------
    230.     degree: int
    231.         The degree of the polynomial that the independent variable X will be transformed to.
    232.     reg_factor: float
    233.         The factor that will determine the amount of regularization and feature
    234.         shrinkage. 
    235.     l1_ration: float
    236.         Weighs the contribution of l1 and l2 regularization.
    237.     n_iterations: float
    238.         The number of training iterations the algorithm will tune the weights for.
    239.     learning_rate: float
    240.         The step length that will be used when updating the weights.
    241.     """
    242.     def __init__(self, degree=1, reg_factor=0.05, l1_ratio=0.5, n_iterations=3000, 
    243.                 learning_rate=0.01):
    244.         self.degree = degree
    245.         self.regularization = l1_l2_regularization(alpha=reg_factor, l1_ratio=l1_ratio)
    246.         super(ElasticNet, self).__init__(n_iterations, 
    247.                                         learning_rate)
    248.  
    249.     def fit(self, X, y):
    250.         X = normalize(polynomial_features(X, degree=self.degree))
    251.         super(ElasticNet, self).fit(X, y)
    252.  
    253.     def predict(self, X):
    254.         X = normalize(polynomial_features(X, degree=self.degree))
    255.         return super(ElasticNet, self).predict(X)

    套索回归代码（从零实现）

    1. from __future__ import print_function, division
    2. import numpy as np
    3. import math
    4. from mlfromscratch.utils import normalize, polynomial_features
    5.  
    6. class l1_regularization():
    7.     """ Regularization for Lasso Regression """
    8.     def __init__(self, alpha):
    9.         self.alpha = alpha
    10.     
    11.     def __call__(self, w):
    12.         return self.alpha * np.linalg.norm(w)
    13.  
    14.     def grad(self, w):
    15.         return self.alpha * np.sign(w)
    16.  
    17. class l2_regularization():
    18.     """ Regularization for Ridge Regression """
    19.     def __init__(self, alpha):
    20.         self.alpha = alpha
    21.     
    22.     def __call__(self, w):
    23.         return self.alpha * 0.5 *  w.T.dot(w)
    24.  
    25.     def grad(self, w):
    26.         return self.alpha * w
    27.  
    28. class l1_l2_regularization():
    29.     """ Regularization for Elastic Net Regression """
    30.     def __init__(self, alpha, l1_ratio=0.5):
    31.         self.alpha = alpha
    32.         self.l1_ratio = l1_ratio
    33.  
    34.     def __call__(self, w):
    35.         l1_contr = self.l1_ratio * np.linalg.norm(w)
    36.         l2_contr = (1 - self.l1_ratio) * 0.5 * w.T.dot(w) 
    37.         return self.alpha * (l1_contr + l2_contr)
    38.  
    39.     def grad(self, w):
    40.         l1_contr = self.l1_ratio * np.sign(w)
    41.         l2_contr = (1 - self.l1_ratio) * w
    42.         return self.alpha * (l1_contr + l2_contr) 
    43.  
    44. class Regression(object):
    45.     """ Base regression model. Models the relationship between a scalar dependent variable y and the independent 
    46.     variables X. 
    47.     Parameters:
    48.     -----------
    49.     n_iterations: float
    50.         The number of training iterations the algorithm will tune the weights for.
    51.     learning_rate: float
    52.         The step length that will be used when updating the weights.
    53.     """
    54.     def __init__(self, n_iterations, learning_rate):
    55.         self.n_iterations = n_iterations
    56.         self.learning_rate = learning_rate
    57.  
    58.     def initialize_weights(self, n_features):
    59.         """ Initialize weights randomly [-1/N, 1/N] """
    60.         limit = 1 / math.sqrt(n_features)
    61.         self.w = np.random.uniform(-limit, limit, (n_features, ))
    62.  
    63.     def fit(self, X, y):
    64.         # Insert constant ones for bias weights
    65.         X = np.insert(X, 0, 1, axis=1)
    66.         self.training_errors = []
    67.         self.initialize_weights(n_features=X.shape[1])
    68.  
    69.         # Do gradient descent for n_iterations
    70.         for i in range(self.n_iterations):
    71.             y_pred = X.dot(self.w)
    72.             # Calculate l2 loss
    73.             mse = np.mean(0.5 * (y - y_pred)**2 + self.regularization(self.w))
    74.             self.training_errors.append(mse)
    75.             # Gradient of l2 loss w.r.t w
    76.             grad_w = -(y - y_pred).dot(X) + self.regularization.grad(self.w)
    77.             # Update the weights
    78.             self.w -= self.learning_rate * grad_w
    79.  
    80.     def predict(self, X):
    81.         # Insert constant ones for bias weights
    82.         X = np.insert(X, 0, 1, axis=1)
    83.         y_pred = X.dot(self.w)
    84.         return y_pred
    85.  
    86. class LinearRegression(Regression):
    87.     """Linear model.
    88.     Parameters:
    89.     -----------
    90.     n_iterations: float
    91.         The number of training iterations the algorithm will tune the weights for.
    92.     learning_rate: float
    93.         The step length that will be used when updating the weights.
    94.     gradient_descent: boolean
    95.         True or false depending if gradient descent should be used when training. If 
    96.         false then we use batch optimization by least squares.
    97.     """
    98.     def __init__(self, n_iterations=100, learning_rate=0.001, gradient_descent=True):
    99.         self.gradient_descent = gradient_descent
    100.         # No regularization
    101.         self.regularization = lambda x: 0
    102.         self.regularization.grad = lambda x: 0
    103.         super(LinearRegression, self).__init__(n_iterations=n_iterations,
    104.                                             learning_rate=learning_rate)
    105.     def fit(self, X, y):
    106.         # If not gradient descent => Least squares approximation of w
    107.         if not self.gradient_descent:
    108.             # Insert constant ones for bias weights
    109.             X = np.insert(X, 0, 1, axis=1)
    110.             # Calculate weights by least squares (using Moore-Penrose pseudoinverse)
    111.             U, S, V = np.linalg.svd(X.T.dot(X))
    112.             S = np.diag(S)
    113.             X_sq_reg_inv = V.dot(np.linalg.pinv(S)).dot(U.T)
    114.             self.w = X_sq_reg_inv.dot(X.T).dot(y)
    115.         else:
    116.             super(LinearRegression, self).fit(X, y)
    117.  
    118. class LassoRegression(Regression):
    119.     """Linear regression model with a regularization factor which does both variable selection 
    120.     and regularization. Model that tries to balance the fit of the model with respect to the training 
    121.     data and the complexity of the model. A large regularization factor with decreases the variance of 
    122.     the model and do para.
    123.     Parameters:
    124.     -----------
    125.     degree: int
    126.         The degree of the polynomial that the independent variable X will be transformed to.
    127.     reg_factor: float
    128.         The factor that will determine the amount of regularization and feature
    129.         shrinkage. 
    130.     n_iterations: float
    131.         The number of training iterations the algorithm will tune the weights for.
    132.     learning_rate: float
    133.         The step length that will be used when updating the weights.
    134.     """
    135.     def __init__(self, degree, reg_factor, n_iterations=3000, learning_rate=0.01):
    136.         self.degree = degree
    137.         self.regularization = l1_regularization(alpha=reg_factor)
    138.         super(LassoRegression, self).__init__(n_iterations, 
    139.                                             learning_rate)
    140.  
    141.     def fit(self, X, y):
    142.         X = normalize(polynomial_features(X, degree=self.degree))
    143.         super(LassoRegression, self).fit(X, y)
    144.  
    145.     def predict(self, X):
    146.         X = normalize(polynomial_features(X, degree=self.degree))
    147.         return super(LassoRegression, self).predict(X)
    148.  
    149. class PolynomialRegression(Regression):
    150.     """Performs a non-linear transformation of the data before fitting the model
    151.     and doing predictions which allows for doing non-linear regression.
    152.     Parameters:
    153.     -----------
    154.     degree: int
    155.         The degree of the polynomial that the independent variable X will be transformed to.
    156.     n_iterations: float
    157.         The number of training iterations the algorithm will tune the weights for.
    158.     learning_rate: float
    159.         The step length that will be used when updating the weights.
    160.     """
    161.     def __init__(self, degree, n_iterations=3000, learning_rate=0.001):
    162.         self.degree = degree
    163.         # No regularization
    164.         self.regularization = lambda x: 0
    165.         self.regularization.grad = lambda x: 0
    166.         super(PolynomialRegression, self).__init__(n_iterations=n_iterations,
    167.                                                 learning_rate=learning_rate)
    168.  
    169.     def fit(self, X, y):
    170.         X = polynomial_features(X, degree=self.degree)
    171.         super(PolynomialRegression, self).fit(X, y)
    172.  
    173.     def predict(self, X):
    174.         X = polynomial_features(X, degree=self.degree)
    175.         return super(PolynomialRegression, self).predict(X)
    176.  
    177. class RidgeRegression(Regression):
    178.     """Also referred to as Tikhonov regularization. Linear regression model with a regularization factor.
    179.     Model that tries to balance the fit of the model with respect to the training data and the complexity
    180.     of the model. A large regularization factor with decreases the variance of the model.
    181.     Parameters:
    182.     -----------
    183.     reg_factor: float
    184.         The factor that will determine the amount of regularization and feature
    185.         shrinkage. 
    186.     n_iterations: float
    187.         The number of training iterations the algorithm will tune the weights for.
    188.     learning_rate: float
    189.         The step length that will be used when updating the weights.
    190.     """
    191.     def __init__(self, reg_factor, n_iterations=1000, learning_rate=0.001):
    192.         self.regularization = l2_regularization(alpha=reg_factor)
    193.         super(RidgeRegression, self).__init__(n_iterations, 
    194.                                             learning_rate)
    195.  
    196. class PolynomialRidgeRegression(Regression):
    197.     """Similar to regular ridge regression except that the data is transformed to allow
    198.     for polynomial regression.
    199.     Parameters:
    200.     -----------
    201.     degree: int
    202.         The degree of the polynomial that the independent variable X will be transformed to.
    203.     reg_factor: float
    204.         The factor that will determine the amount of regularization and feature
    205.         shrinkage. 
    206.     n_iterations: float
    207.         The number of training iterations the algorithm will tune the weights for.
    208.     learning_rate: float
    209.         The step length that will be used when updating the weights.
    210.     """
    211.     def __init__(self, degree, reg_factor, n_iterations=3000, learning_rate=0.01, gradient_descent=True):
    212.         self.degree = degree
    213.         self.regularization = l2_regularization(alpha=reg_factor)
    214.         super(PolynomialRidgeRegression, self).__init__(n_iterations, 
    215.                                                         learning_rate)
    216.  
    217.     def fit(self, X, y):
    218.         X = normalize(polynomial_features(X, degree=self.degree))
    219.         super(PolynomialRidgeRegression, self).fit(X, y)
    220.  
    221.     def predict(self, X):
    222.         X = normalize(polynomial_features(X, degree=self.degree))
    223.         return super(PolynomialRidgeRegression, self).predict(X)
    224.  
    225. class ElasticNet(Regression):
    226.     """ Regression where a combination of l1 and l2 regularization are used. The
    227.     ratio of their contributions are set with the 'l1_ratio' parameter.
    228.     Parameters:
    229.     -----------
    230.     degree: int
    231.         The degree of the polynomial that the independent variable X will be transformed to.
    232.     reg_factor: float
    233.         The factor that will determine the amount of regularization and feature
    234.         shrinkage. 
    235.     l1_ration: float
    236.         Weighs the contribution of l1 and l2 regularization.
    237.     n_iterations: float
    238.         The number of training iterations the algorithm will tune the weights for.
    239.     learning_rate: float
    240.         The step length that will be used when updating the weights.
    241.     """
    242.     def __init__(self, degree=1, reg_factor=0.05, l1_ratio=0.5, n_iterations=3000, 
    243.                 learning_rate=0.01):
    244.         self.degree = degree
    245.         self.regularization = l1_l2_regularization(alpha=reg_factor, l1_ratio=l1_ratio)
    246.         super(ElasticNet, self).__init__(n_iterations, 
    247.                                         learning_rate)
    248.  
    249.     def fit(self, X, y):
    250.         X = normalize(polynomial_features(X, degree=self.degree))
    251.         super(ElasticNet, self).fit(X, y)
    252.  
    253.     def predict(self, X):
    254.         X = normalize(polynomial_features(X, degree=self.degree))
    255.         return super(ElasticNet, self).predict(X)

  • 相关阅读:
    什么是JSON
    软件测试工程师的职场发展顺序，月薪30k的测试岗技术要求是真的高...
    前端入门学习笔记三十八
    单页应用（SPA）和多页应用（MPA）的区别和优缺点？
    深入理解Spring Boot AOP：CGLIB代理与JDK动态代理的完全指南
    【面试题精讲】什么是websocket？如何与前端通信？
    解读PowerJob的秘密武器：探索Akka Toolkit原理
    「Java开发指南」如何利用MyEclipse启用Spring DSL？（二）
    [答疑]角色和状态的区别
    html+css仿制小米商城首页
  • 原文地址：https://blog.csdn.net/sikh_0529/article/details/126885307