-
一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法 -附代码
一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法
摘要:为克服基本樽海鞘群算法(SSA)存在的收敛速度慢、易陷入局部最优等不足,提出了一种基于折射反向学习和自适应控制因子的新型改进樽海鞘群算法(RCSSA).首先,采用折射反向学习机制在每一次个体的求解中计算折射反向解,极大地提高了算法收敛精度和速度.然后,将原SSA算法中引导者的自适应控制因子引入跟随者的位置更新中,有效地控制整个搜索过程并增加了算法的局部开发能力.1.樽海鞘群算法
基础樽海鞘群算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107767869
2.改进樽海鞘群算法
2.1 折射反向学习机制
当优化问题的空间维度增加时, 折射反 向学习解可按下式计算
x i , j ∗ = a j + b j 2 + a j + b j 2 k − x i , j k . (10) x_{i, j}^*=\frac{a_j+b_j}{2}+\frac{a_j+b_j}{2 k}-\frac{x_{i, j}}{k} . \tag{10} xi,j∗=2aj+bj+2kaj+bj−kxi,j.(10)
式中: x i , j x_{i, j} xi,j 表示当前种群中第 i i i 个体在第 j j j 维上位置, x i , j ∗ x_{i, j}^* xi,j∗ 为 x i , j x_{i, j} xi,j 的折射反向解, a j a_j aj 和 b j b_j bj 分别为搜索空间上第 j j j 维的最小值和最大值.2.2 自适应控制因子
在原 SSA 算法中, 随着算法的迭代进化, 楢海 輎群体中的引导者不断向食物源移动, 其余追随者 依次相连, 逐渐向种群中适应度较优的引导者靠扰. 然而, 从式 (3) 中可看到, 追随者的位置只跟自身和 相邻个体的位置相关, 其行为较为单一. 因此, 当种 群中的引领者陷入局部最优时, 追随者必然随之陷 入局部最优, 从而导致算法出现古熟收敛现象.
前文已经提到: 控制因子 c 1 c_1 c1 随着迭代次数的增 加, 从 2 非线性降低到趋于 0 . 这样的变化有利于算 法在迭代初期进行全局探索,在迭代后期能够在局 部进行开发. 为此, 本文提出将控制因子 c 1 c_1 c1 引入追随 者的位置更新, 此时追随者也能够与引导者一样, 产 生自适应更新, 从而提高算法跳出局部最优的能力, 并加快整体的收敛速度. 新的追随者公式为
x i , j = c 1 2 ( x i , j + x i − 1 , j ) . (11) x_{i, j}=\frac{c_1}{2}\left(x_{i, j}+x_{i-1, j}\right) .\tag{11} xi,j=2c1(xi,j+xi−1,j).(11)
其中 c 1 c_1 c1 的表达式见式 (2).RCSSA 算法实现流程如下:
Step1:设置算法参数:种群规模 N N N, 最大帙代次 数 T T T,搜索维数 D D D, 掜索范围 [ l b , u b ] [l b, u b] [lb,ub]; 随机生成樽海 脒种群;
Step 2 \operatorname{Step} 2 Step2 : 计算每个个体的适应度值, 将适应度值 最、的个体位置作为食物源;Step3: 更新控制因子 c 1 c_1 c1, 判断种群数是否超过 N / 2 N / 2 N/2 : 超讨则进入 Step5, 否则进入 Step4;
Step4:更新随机数 c 2 、 c 3 c_2 、 c_3 c2、c3 ,根据式 (1) 更新每个 引导者个体的位置,同时采用式(10)计算其折射反 向解, 比较二者适应度大小, 取较小的一个个体为新 的位置, 并进入 Step6;
Step5:根据式 (3) 更新每个追随者个体的位置, 采用引入控制因子 c 1 c_1 c1 的式 (11) 计算其折射反向解, 比 较二者适应度大小, 取较小的一个个体为新的位置;
Step6:比较食物源和当前棏海革肖最优个体的适 应度大小, 取䢂小的一个为新的食物源;Step7:若当代迭代次数讴到最大迭代次数 T T T, 则输出最优个体, 即算法找到的最优解; 否则, 返回 Step2.
3.实验结果
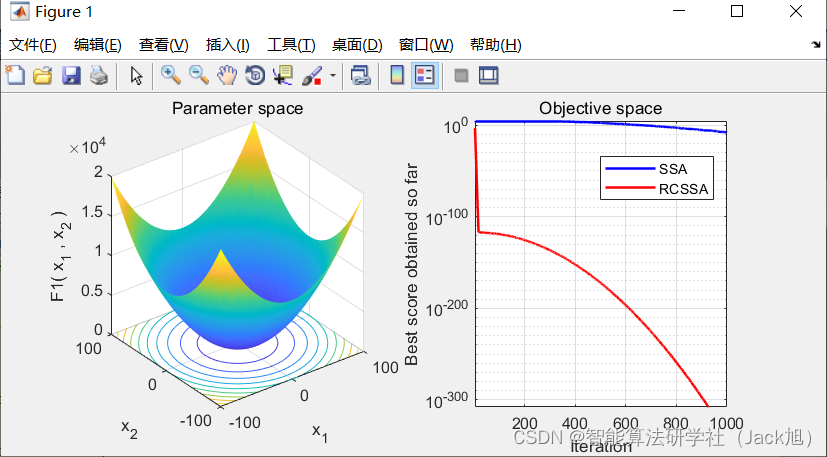
4.参考文献
[1]范千,陈振健,夏樟华.一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法[J].哈尔滨工业大学学报,2020,52(10):183-191.
5.Matlab代码
6.python代码
-
相关阅读:
视频清晰度优化指南
Android 11.0修改系统默认设备类型的平板电脑类型为设备类型
IfcOpenShell - Python 2022最新安装步骤 兼谈IFC的理解与认识
WebDAV之π-Disk派盘 + 天天
make命令常用选项 + gcc 常用选项
HTML期末大作业——游戏介绍(HTML+CSS+JavaScript) web前端开发技术 web课程设计网页规划与设计 Web大学生网页成品
想要裸辞做电商,有什么好的建议吗?做哪类产品比较好?
海康G5系列(armv7l) heop模式下交叉编译Qt qmqtt demo,出现moc缺少高版本GLibc问题之解决
RP9学习-1
A,B=input().split(“,“)A=eval(A)A=str(A)B=eval(B)print(A*B)
- 原文地址:https://blog.csdn.net/u011835903/article/details/126883208