前端开发面试-js排序实现

思路：冒泡排序，len个元素，需要len-1趟比较就可以得到最终的排序
第一趟比较过后，会得到一个最大值或者一个最小值， 第二趟比较后同理得到第二个最大或者最小值
如果想要前面有序，需要从后面开始两两比较，将最小值替换到前面，最终将得到的最小值冒泡到最前面的位置

如果想往前冒泡，需要从后面开始两两比较
若为逆序，则交换他们，直到序列比较完，第一趟冒泡完成，得到最小值

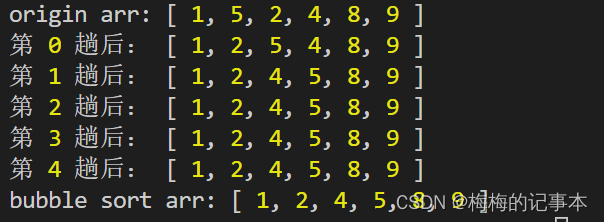
function bubbleSort(arr) {
    console.log('origin arr:', arr)
    let len = arr.length
    for (let i = 0; i < len - 1; i++) {
        for (let j = len - 1; j > i; j--) {
            //如果前面的元素小于后面的元素，交换
            //也就是说把大的值往前冒泡
            if (arr[j - 1] > arr[j]) {
                [arr[j - 1], arr[j]] = [arr[j], arr[j - 1]]
            }
        }
    }
    console.log('bubble sort arr:', arr)
    return arr
}
bubbleSort([1, 5, 2, 4, 8, 9])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

思路：在待排序中取一个值作为基准记录（一般取第一个元素），然后从后往前遍历，找到一个位置，使得待排序数组分成两个部分，这个位置前面的元素值都小于等于这个基准记录；这个位置后面的元素值都大于等于这个基准记录，同时把这个基准记录放到这个位置上。至此第一趟完成。第二趟同理，直到分为一个元素为止。一共n个记录所以需要以log2为底n的对数 趟。

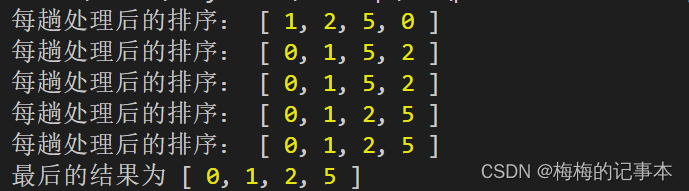
//先找到分割点
function getIndex(arr, low, high) {
    let pivot = arr[low]  //把最小值赋值给枢纽，这块位置就空出来了
    while (low < high) {  //当low==high就找到了枢纽值要放的位置 
        while (low < high && arr[high] >= pivot) {   //只有比枢纽值小才动，相等不动，保证了稳定性
            high--
        }
        arr[low] = arr[high]
        while (low < high && arr[low] <= pivot) {  //只有比枢纽值大才动
            low++
        }
        arr[high] = arr[low]
    }
    arr[low] = pivot     //枢纽值放在最终空出来的位置
    return low
}
function quickSort(arr, low, high) {
    if (low < high) {
        let dex = getIndex(arr, low, high)
        quickSort(arr, low, dex - 1)   //递归调用
        quickSort(arr, dex + 1, high)
    }
    return arr  //注意要有返回值，不然会报错
}
let arr = [1, 2, 5, 0]
let ar = quickSort(arr, 0, arr.length - 1)
console.log(ar)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

思路：将整个记录分为两个部分：有序区和无序区，有序区在左侧，无序区在右侧，初始时有序区为空，无序区为n个记录，每次从无序区中找出最小值然后和前面的元素交换，直到所有的元素有序

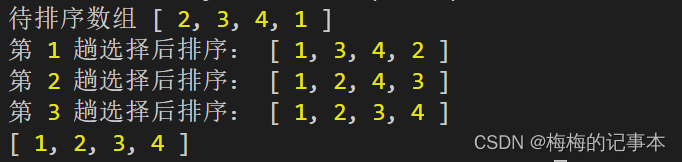
function simpleSelect(arr) {
    // arr.length-1趟比较
    for (let i = 0; i < arr.length - 1; i++) {
        // 记录最小值
        let k = i
        for (let j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[k]) {
                k = j
            }
        }
        if (k !== i) { //arr[i]不是最小值了，要进行交换
            [arr[k], arr[i]] = [arr[i], arr[k]]
        }
    }
    return arr
}
let arr = [2, 3, 4, 1]
console.log(simpleSelect(arr))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

堆的定义：
堆其实是特殊的树。只要满足这两点，它就是一个堆。
1.堆是一个完全二叉树。完全二叉树：除了最后一层，其他层的节点数都是满的，最后一层的节点都靠左排列
2.堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。也可以说：堆中每个节点的值都大于等于（或小于等于）其左右子节点的值。两种表述一样的。
对于每个节点的值都大于等于子树中每一个节点的值，叫做大顶堆。
对于每个节点的值都小于等于子树中每一个节点的值，叫做小顶堆。
思路：首先从Math.floor(arr.length/2-1)位置即非叶子结点开始进行递归方式进行大根堆排序，调整得到大根堆，
然后根元素和最后一个元素进行交换，交换后，得到最后一个元素是最大值且有序，前n-1个元素不是大根堆了，
此时从根元素进行调整得到大根堆（有一个注意点，这里只要进行交换就要对这个交换的节点重新进行调整，
也是一个递归的过程），然后根元素和最后一个元素交换，此时的最后两个元素是有序的，前n-2个元素继续调整为
大根堆，以此类推，
还有一个注意点：在调整的函数里面，是直接把数组当成堆了，然后操作的是直接对数组下标操作的

//构建堆
let heapify = (arr,n,i)=>{
    let largest = i  //将当前节点进行保存，初始化为根
    let  left = 2*i+1 //定位到当前节点的左边的子节点
    let right = 2*i+2  //当前节点的右边子节点
    if(left<n &&arr[left]>arr[largest]){
        largest = left
    }
    if(right<n && arr[right]>arr[largest]){
        largest = right
    }
    if(largest !==i){
        let swap = arr[i]
        arr[i] = arr[largest]
        arr[largest] = swap
        //和左边或者右边的子节点交换完了，左边或右边的孩子节点又不是大根堆了
        //堆和根节点交换的那个节点 继续和它的左右进行比较
        //有节点调整了，就要重新调用这个函数进行调整
        heapify(arr,n,largest)
    }
}
let sort = (arr)=>{
    let n = arr.length
    //第一次构建大根堆，要从最后一个拥有子节点的节点开始，将该节点连同其子节点进行比较
    //将最大的数交换与该节点，交换后，再依次向前节点进行相同的比较
    //直至构建出大根堆
    //[1,5,3,4,10]
    //第一次i=Math.floor(n/2-1)=1 对应数组中5 此时构建的大根堆[1,10,3,4,5]
    //第二次i-- 此时i=0 对应数组中1 此时构建的大根堆[10,5,3,4,1](调用heapify此时这块是递归的，只要有节点调整了就会继续调用调整)
    for(let i=Math.floor(n/2-1);i>=0;i--){
        heapify(arr,n,i)
    }
    //上面调整后的堆顶永远是最大元素，所以将堆顶和最后一个元素交换
    //第一次交换完最后一个元素为最大值，前n-1个元素重新调整
    //第二次交换完还是和最后一个元素交换，那么后两个元素是从大到小有序的，然后前n-2个元素重新调整
    for(let i=n-1;i>0;i--){
        let temp = arr[0]
        arr[0] = arr[i]
        arr[i] = temp
        //根和最后一个元素交换完成后，前n-1个元素又不是大根堆了 要重新进行调整到大根堆
        heapify(arr,i,0)
    }
}
let elements = [3, 1, 5, 7, 2, 4, 9, 6, 10, 8];
    console.log('before: ' + elements);
    sort(elements);
    console.log(' after: ' + elements);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

将待排序的元素，插入到有序中的恰当位置，过程中涉及查找和插入，由于查找的方式不一样，所以分为 ：直接插入法，二分插入法和希尔排序

思路：每一趟都是将一个元素记录插入到有序的数组中的恰当位置。首先第一个元素已经有序了，从第二个元素开始进行判断，从前面有序的数组的最后一个元素开始比较，假设结果为升序，如果要插入的元素比有序区的小，将有序区的元素往后移动，直到找到插入元素的位置。因为要将元素插入到有序区时涉及到元素移动覆盖了要插入的元素，所以利用一个guard临时保存一下这个值。

//插入排序，将一个记录插入到已经排好序的有序列表，从而得到一个新的有序列表
function insert(arr){
   //第一个位置的元素肯定有序了，从第二个元素开始往后遍历
  for(let i=1;i<arr.length;i++){
    let j = i-1
     //保存一下这个记录，以便于 前面有序的比他小的元素 往后移动
    let guard = arr[i]
    //假如第二个元素比第一个元素小，肯定需要往前移动，比前一个有序的元素大，那么它就不需要移动位置了
    for(;guard<arr[j];j--){ //此时arr[j]==guard的时候 就不移动元素了，说明这个也是一个稳定的排序
      arr[j+1] = arr[j]//j的位置放在j+1的位置，最终空出来的也是j+1的位置 就是要插入的位置
    }
    arr[j+1] = guard
  }
  return arr
}
console.log(insert([2,3,1,4]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

思路：查找和插入，查找位置的过程中利用二分在有序数组中查找位置。
需要注意点：是查找位置的时候，注意左边界和有边界的选取

/**
 * 返回值为val在有序数组中的位置
 * @param {数组} arr 
 * @param {有序数组的左边界} left 
 * @param {有序数组的有边界} right 
 * @param {要查找val的位置} val 
 */
// // 采用最普通的二分处理
function getPosition(arr, left, right, val) {
    while (left <= right) {
        let mid = Math.floor((right + left) / 2)
        if (val < arr[mid]) {
            right = mid - 1
        } else if (val > arr[mid]) {
            left = mid + 1
        } else if (val == arr[mid]) {
            return mid
        }
    }
    return left
}

function binaryInsert(arr) {
    let len = arr.length
    for (let i = 1; i < len; i++) {
        //记录要插入的元素arr[i]这个值
        let temp = arr[i]
        // 注意这里的有序区是下标为0到i-1在这个区间内找位置
        let pos = getPosition(arr, 0, i - 1, temp)
        for (let j = i - 1; j >= pos; j--) {
            arr[j + 1] = arr[j]
        }
        arr[pos] = temp
    }
    return arr

}
let arr = [2, 1, 5, 4, 4]
console.log(binaryInsert(arr))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

希尔排序：是插入排序的一种，又叫做减小增量法排序。　对于ｎ个记录，选取一个间隔gap,作为间隔增量，然后将下标为0，gap,2gap,2gap…进行插入排序，将1，gap+1，2gap+1，3gap+1…进行插入排序。
然后再对gap进行gap=gap/2 进行上述的插入排序
直到gap值为1 进行插入排序后得到的为排序后的结果
因为时间复杂度取决于gap的选取，所以只有平均复杂度 n的1.3次幂

/**
 * @param {使用希尔排序给定数组进行排序} arr 
 */
function shell(arr) {
    let len = arr.length
    // 增量gap初始值为长度的一半
    for (let gap = Math.floor(len / 2); gap >= 1; gap = Math.floor(gap / 2)) {
        //对于增量为gap的元素进行插入排序
        //第一个元素(第一个gap区间，即下标为0-gap)已经有序，从第二个开始进行插入排序
        for (let i = gap + 1; i < len; i++) {
            let temp = arr[i]
            let j = i - gap
            while (arr[j] > temp) {
                arr[j + gap] = arr[j]
                j = j - gap
            }
            arr[j + gap] = temp
        }
    }
    return arr
}
let arr = [1, 3, 2, 4, 6]
console.log(shell(arr))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

思路：假设初始序列含有n个记录，则可以看成n个有序的子序列，每个子序列的长度为1，然后两两归并，得到（>=n/2）个长度为2或1 的有序子序列，再两两归并，直到得到一个长度为n的有序序列为止，这就叫2路归并。

const mergesort = arr=>{
    const len = arr.length
    if(len < 2){
        return arr
    }
    let mid = Math.floor(len/2)  //js里面 3/2=1.5
    let left = arr.slice(0,mid) //slice左闭右开
    let right = arr.slice(mid)
    return merge(mergesort(left),mergesort(right))
}
let merge = (left,right)=>{
    const res = []
    while(left.length && right.length){
        if(left[0]<=right[0]){
            res.push(left.shift())  //shift操作改变原数组
        }else{
            res.push(right.shift())
        }
    }
    while(left.length) res.push(left.shift());
    while(right.length) res.push(right.shift());
    return res
}
let arr = [2,3,4,1,5,6,8,7,9]
//console.time,console.timeEnd这两个方法可以用来测量JavaScript脚本程序执行消耗的时间。
//都可以传入一个参数，作为计时器的名称，用来区分各个计时器
//注意一点：这两个参数名称要一致
console.time('归并排序消耗时间') //启动计时器
console.log(mergesort(arr))
console.timeEnd('归并排序消耗时间') //停止计时，输出时间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

思路： 留坑TODO

1