2022年高教社杯国赛A题思路——波浪能最大输出功率设计

1 A题: 波浪能最大输出功率设计

随着经济和社会的发展，人类面临能源需求和环境污染的双重挑战，发展可再生能源产业
已成为世界各国的共识。波浪能作为一种重要的海洋可再生能源，分布广泛，储量丰富，具有
可观的应用前景。波浪能装置的能量转换效率是波浪能规模化利用的关键问题之一。

图 1 为一种波浪能装置示意图，由浮子、振子、中轴以及能量输出系统（PTO，包括弹簧
和阻尼器）构成，其中振子、中轴及 PTO 被密封在浮子内部；浮子由质量均匀分布的圆柱壳体
和圆锥壳体组成；两壳体连接部分有一个隔层，作为安装中轴的支撑面；振子是穿在中轴上的
圆柱体，通过 PTO 系统与中轴底座连接。在波浪的作用下，浮子运动并带动振子运动（参见附
件 1 和附件 2），通过两者的相对运动驱动阻尼器做功，并将所做的功作为能量输出。考虑海
水是无粘及无旋的，浮子在线性周期微幅波作用下会受到波浪激励力（矩）、附加惯性力（矩）、
兴波阻尼力（矩）和静水恢复力（矩）。在分析下面问题时，忽略中轴、底座、隔层及 PTO 的
质量和各种摩擦。

请建立数学模型解决以下问题：

问题 1

如图 1 所示，中轴底座固定于隔层的中心位置，弹簧和直线阻尼器一端固定在振
子上，一端固定在中轴底座上，振子沿中轴做往复运动。直线阻尼器的阻尼力与浮子和振子的
相对速度成正比，比例系数为直线阻尼器的阻尼系数。考虑浮子在波浪中只做垂荡运动（参见
附件 1），建立浮子与振子的运动模型。初始时刻浮子和振子平衡于静水中，利用附件 3 和附
件 4 提供的参数值（其中波浪频率取 1.4005 s−1，这里及以下出现的频率均指圆频率，角度均
采用弧度制），分别对以下两种情况计算浮子和振子在波浪激励力 𝑓 cos 𝜔𝑡（𝑓 为波浪激励力
振幅，𝜔 为波浪频率）作用下前 40 个波浪周期内时间间隔为 0.2 s 的垂荡位移和速度：(1) 直
线阻尼器的阻尼系数为 10000 N·s/m；(2) 直线阻尼器的阻尼系数与浮子和振子的相对速度的绝
对值的幂成正比，其中比例系数取 10000，幂指数取 0.5。将结果存放在 result1-1.xlsx 和
result1-2.xlsx 中。在论文中给出 10 s、20 s、40 s、60 s、100 s 时，浮子与振子的垂荡位移和速
度。

问题 2

仍考虑浮子在波浪中只做垂荡运动，分别对以下两种情况建立确定直线阻尼器的
最优阻尼系数的数学模型，使得 PTO 系统的平均输出功率最大：(1) 阻尼系数为常量，阻尼系
数在区间 [0,100000] 内取值；(2) 阻尼系数与浮子和振子的相对速度的绝对值的幂成正比，比
例系数在区间 [0,100000] 内取值，幂指数在区间 [0,1] 内取值。利用附件 3 和附件 4 提供的
参数值（波浪频率取 2.2143 s−1）分别计算两种情况的最大输出功率及相应的最优阻尼系数。

问题 3

如图 2 所示，中轴底座固定于隔层的中心位置，中轴架通过转轴铰接于中轴底座
中心，中轴绕转轴转动，PTO 系统连接振子和转轴架，并处于中轴与转轴所在的平面。除了直
线阻尼器，在转轴上还安装了旋转阻尼器和扭转弹簧，直线阻尼器和旋转阻尼器共同做功输出
能量。在波浪的作用下，浮子进行摇荡运动，并通过转轴及扭转弹簧和旋转阻尼器带动中轴转
动。振子随中轴转动，同时沿中轴进行滑动。扭转弹簧的扭矩与浮子和振子的相对角位移成正
比，比例系数为扭转弹簧的刚度。旋转阻尼器的扭矩与浮子和振子的相对角速度成正比，比例
系数为旋转阻尼器的旋转阻尼系数。考虑浮子只做垂荡和纵摇运动（参见附件 2），建立浮子
与振子的运动模型。初始时刻浮子和振子平衡于静水中，利用附件 3 和附件 4 提供的参数值（波
浪频率取 1.7152 s−1），假定直线阻尼器和旋转阻尼器的阻尼系数均为常量，分别为 10000 N·s/m
和 1000 N·m·s，计算浮子与振子在波浪激励力和波浪激励力矩 𝑓 cos 𝜔𝑡，𝐿 cos 𝜔𝑡（𝑓 为波浪激
励力振幅，𝐿 为波浪激励力矩振幅，𝜔 为波浪频率）作用下前 40 个波浪周期内时间间隔为 0.2
s 的垂荡位移与速度和纵摇角位移与角速度。将结果存放在 result3.xlsx 中。在论文中给出 10 s、
20 s、40 s、60 s、100 s 时，浮子与振子的垂荡位移与速度和纵摇角位移与角速度。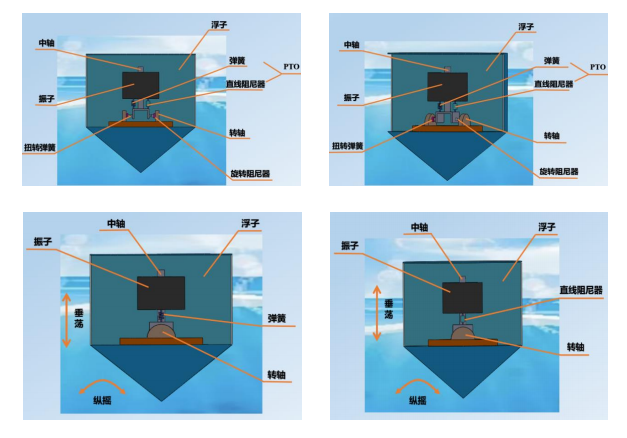

问题 4
考虑浮子在波浪中只做垂荡和纵摇的情形，针对直线阻尼器和旋转阻尼器的阻尼
系数均为常量的情况，建立确定直线阻尼器和旋转阻尼器最优阻尼系数的数学模型，直线阻尼
器和旋转阻尼器的阻尼系数均在区间 [0,100000] 内取值。利用附件 3 和附件 4 提供的参数值
（波浪频率取 1.9806 s−1）计算最大输出功率及相应的最优阻尼系数。

• 附件 1 垂荡的动画

• 附件 2 垂荡和纵摇的动画

• 附件 3 不同入射波浪频率下的附加质量、附加转动惯量、兴波阻尼系数、波浪激励力（矩）
  振幅

• 附件 4 浮子和振子的物理参数和几何参数值

• 附录 术语

  • 浮体在波浪的作用下做摇荡运动时，会受到海水的作用，包括附加惯性力（矩）、兴波阻
    尼力（矩）和静水恢复力（矩）。
  • 附加惯性力（矩） 推动浮体做摇荡运动的力（矩）不仅要推动浮体运动，还要推动浮体
    周围的流体运动。因此，要使浮体在海水中获得（角）加速度，需要施加额外的力（矩），称
    为附加惯性力（矩）。附加惯性力（矩）对应产生一个虚拟质量（虚拟转动惯量），即为附加
    质量（附加转动惯量）。
  • 兴波阻尼力（矩） 浮体在海水中做摇荡运动时，会兴起波浪，从而产生对浮体摇荡运动
    的阻力（矩），称为兴波阻尼力（矩）。兴波阻尼力（矩）与摇荡运动的（角）速度成正比，
    方向相反，比例系数称为兴波阻尼系数。
  • 静水恢复力 浮体在海水中做垂荡运动时，会受到使浮体回到平衡位置的作用力，称为静
    水恢复力。静水恢复力实际上是由浮体在垂荡运动时所受到的浮力变化引起的。
  • 静水恢复力矩 浮体在海水中做纵摇运动时，会受到使浮体转正的力矩，称为静水恢复力
    矩，其大小与浮体相对于静水面的转角成正比，比例系数称为静水恢复力矩系数。

2 解题思路

从整体上来看

A题 波浪能最大输出功率设计

此题属于传统的物理类题目，需要过硬的专业技能和计算能力。需要模拟仿真的能力，此题建议相关专业同学选择，由于所有指标都给的很明确，所以存在最优解（可能是一个范围值）。建议在最后对对答案，答案的正确与否会对最终成绩产生较大影响。推荐物理学、电气工程、数学等相关专业选择。难度较高，开放度较低。

B题 无人机遂行编队飞行中的纯方位无源定位

题型比较常见，在过去的数模竞赛中，已经出现了很多次关于无人机的调度等问题，这次是关于定位的问题。问题的核心在于如何以更少的信号源（无人机发射信号），使得实现无人机的有效定位，建议使用仿真模拟的方式，逐一增加信号源，计算其定位。这道题目中，由于各个无人机是在持续运动的，所以应该设计一个预判优化模型，使得目标值最小。这道题目适合数学、统计学相关专业的同学选择，难度适中，由于数值都已给定，所以开放度也较低，存在最优解（可能是一个范围值）。建议在最后对对答案，答案的正确与否会对最终成绩产生较大影响。

C题 古代玻璃制品的成分分析与鉴别

这道题就是很多同学在训练的时候经常做的题目类型了，属于大数据、数据分析类题目。需要对玻璃制品的成分进行分析，这里就涉及到需要建立一些评价模型，需要做因子分析、主成分分析等常用的机器学习算法，同时需要一些可视化图来进行支撑。后面更新的C题思路，将会有详细的分析。这道题目推荐所有专业同学选择，门槛较低且开放度也相对较高。