《算法导论》第14章-数据结构的扩张 14.1-动态顺序统计 14.2-如何扩张数据结构

14.1 动态顺序统计

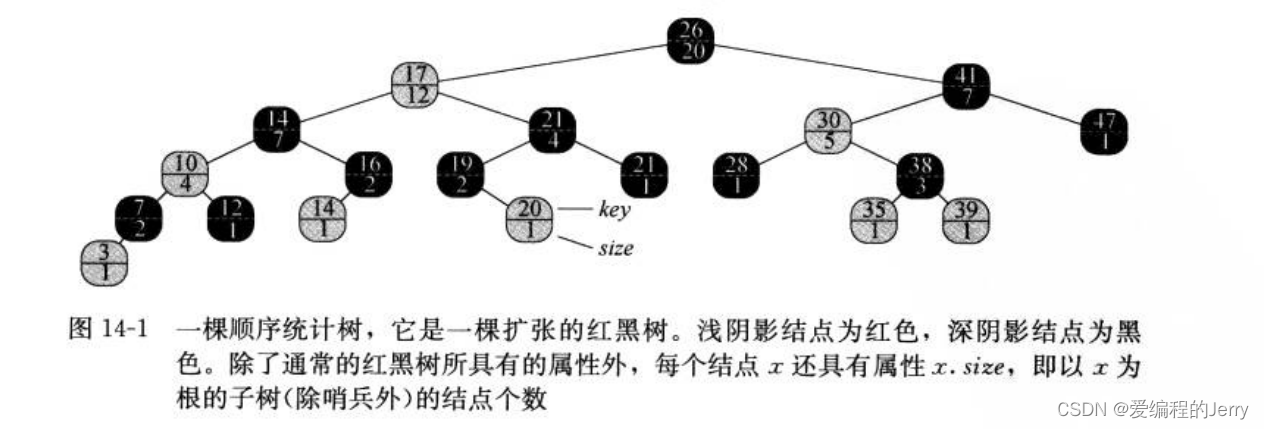
1、顺序统计数：图14-1显示了一种支持快速顺序统计操作的数据结构。顺序统计树(order-statistic tree)T 只
是简单地在每个结点上存储附加信息的一棵红黑树。在红黑树的结点x中，除了通常属性
x.key、x.color、x.p、x.left 和x.right之外，还包括另一个属性x.size。这个属性包含了以x
为根的子树(包括x本身)的(内)结点数，即这棵子树的大小。如果定义哨兵的大小为0，也就是
设置T.nil.size为0，则有等式:
x.size = x.left.size+x.right.size+1

2、秩：在集合线性序中的位置。

查找具有给定秩的元素

OS-SELECT(x,i)
r = x.left.size + 1
if i == r
	return x
elseif i < r
	return OS-SELECT(x,left,i)
else return OS-SELECT(x.right,i-r)
1
2
3
4
5
6
7

确定一个元素的秩

OS-RANK(T,x)
r = x.left.size + 1
y = x
while y != T.root
	//如果y是右结点，那么加上左兄弟结点上的数量再加上父结点（+1）
	if y == y.p.right
		r = r + y.p.left.size + 1
	y = y.p
return r
1
2
3
4
5
6
7
8
9

以上代码

#include 
#include 
using namespace std;
struct RbTreeNode
{
	string color;
	RbTreeNode* left;
	RbTreeNode* right;
	RbTreeNode* parent;
	int value;
	int size;
	RbTreeNode(int x,int y) :value(x),size(y), left(NULL), right(NULL),parent(NULL) {}
};
//引用哨兵机制
struct RbTree
{
	RbTreeNode* root;
	RbTreeNode* nil;
};
//寻找第i小关键字
RbTreeNode *os_select(RbTreeNode* root, int i)
{
	int r = root->left->size + 1;
	if (i == r||root->left->value ==-1||root->right->value==-1) {
		return root;
	}
	else if (i < r) {
		return os_select(root->left, i);
	}
	else {
		return os_select(root->right, i - r);
	}
}
//确定元素的秩
int os_rank(RbTree* T, RbTreeNode* x)
{
	//先加上自己身上的size
	int r = x->left->size + 1;
	RbTreeNode *y = x;
	while (y != T->root) {
		//如果y是右结点，那么加上左兄弟结点上的数量再加上父结点（+1）
		if (y == y->parent->right) {
			r = r + y->parent->left->size + 1;
		}
		y = y->parent;
	}
	return r;
}
int main()
{
	RbTree* T = new RbTree();
	T->nil = new RbTreeNode(-1,-1);
	T->root = new RbTreeNode(4,7);
	T->root->parent = T->nil;
	RbTreeNode* l = new RbTreeNode(2,3);
	T->root->left=l;
	l->parent = T->root;
	RbTreeNode* ll = new RbTreeNode(1,1);
	 l->left=ll;
	 ll->parent = l;
	RbTreeNode* lr = new RbTreeNode(3,1);
	 l->right=lr;
	 ll->parent = l;
	RbTreeNode* r = new RbTreeNode(6,3);
	T->root->right=r;
	r->parent = T->root;
	RbTreeNode* rl = new RbTreeNode(5,1);
	r->left=rl;
	rl->parent = r;
	RbTreeNode* rr = new RbTreeNode(7,1);
	 r->right=rr;
	 rr->parent = r;
	 ll->left = T->nil; ll->right = T->nil;
	 lr->left = T->nil; lr->right = T->nil;
	 rl->left = T->nil; rl->right = T->nil;
	 rr->left = T->nil; rr->right = T->nil;
	cout<< "第i小的数为" << os_select(T->root, 5)->value<<endl;
	cout << "元素的秩为" << os_rank(T,r) << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

14.2 如何扩张数据结构

引入

扩张数据结构分为四步：
1.选择一种基础数据结构。
2.确定基础数据结构中要维护的附加信息。
3.检验基础数据结构上的基本修改操作能否维护附加信息。
4.设计一些新操作。

对红黑树的扩张

定理14. 1(红黑树的扩张)：设f是n个结点的红黑树T扩张的属性，且假设对任一结点x,
f的值仅依赖于结点x、x.left和x.right的信息，还可能包括x.left. f和x.right.f。那么，我
们可以在插入和删除操作期间对T的所有结点的f值进行维护，并且不影响这两个操作的
O(lgn)渐近时间性能。