迪杰斯特拉算法（Java）

第7章 迪杰斯特拉算法

7.1应用场景

用场景

7.2算法介绍

迪杰斯特拉（Dijkstra）算法是典型最短路径算法，用于计算一个顶点到其他顶点的最短路径。它的主要特点是以起始点为中心向外层层扩展（广度优先搜索思想），直到扩展到终点为止。

算法过程

设置出发顶点为v，顶点集合V{ v1， v2,vi …} ，v到V中各顶点的距离构成距离集合Dis，Dis{ d1，d2，di…}，Dis集合记录着b到图中各顶点的距离(到自身距离为0，v 到vi距离对应为di)

1）从Dis中选择值最小的di移出Dis集合，同时移出V集合中对应的顶点vi，此时的v到vi即是最短路径

2）更新Dis集合，更新规则为：比较v到V集合中顶点的距离值，与v通过vi到V集合中顶点的距离值，保留值较小的一个（同时也因该更新顶点的前驱顶点为vi，表明是通过vi到达的）

3重复执行上面两步骤，直到最短路径顶点为目标顶点即可结束。

7.3 算法图解

7.4代码实现

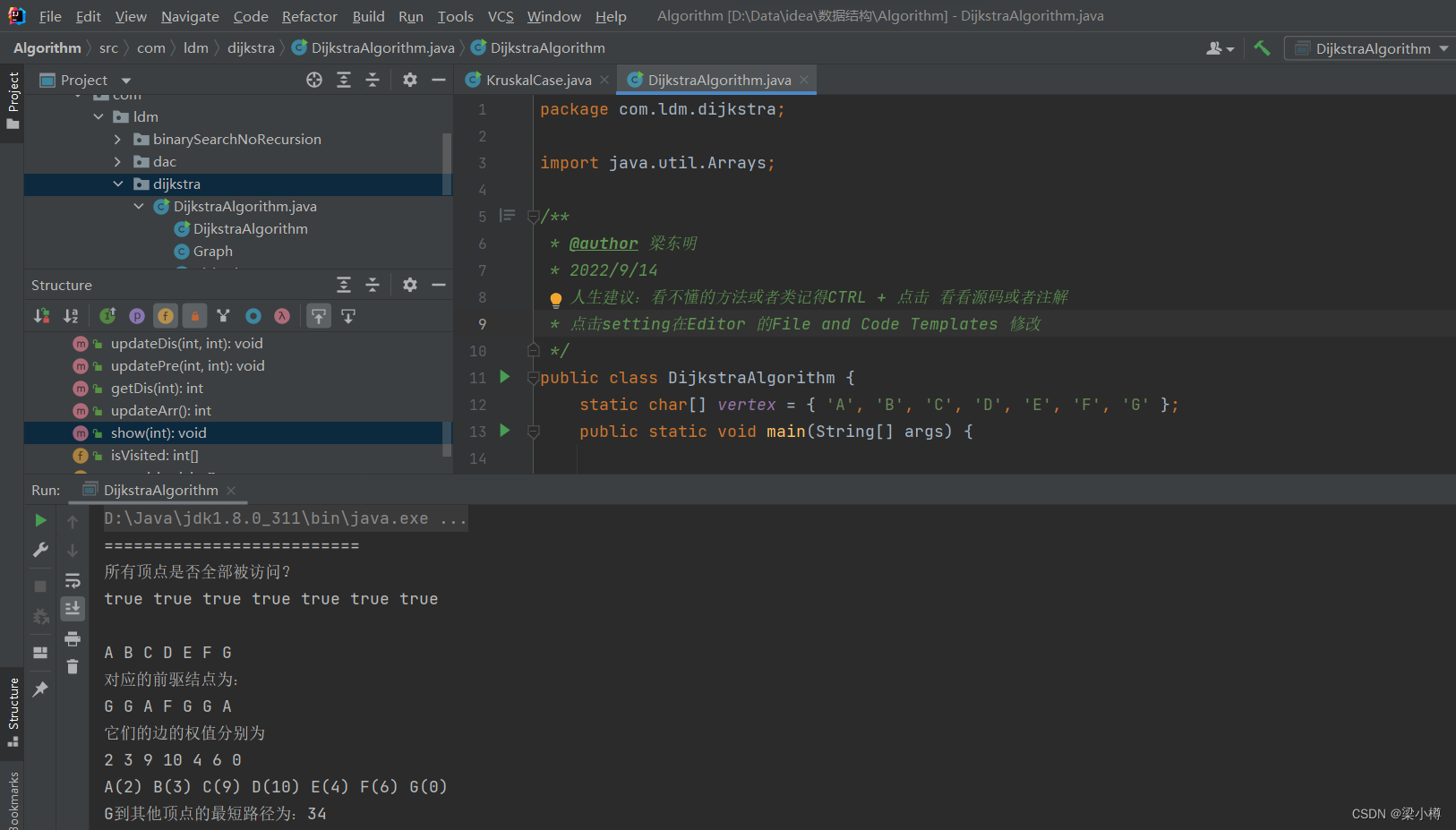别看步骤繁杂，我的代码你只需要修顶点、邻接矩阵和出发点就可以使用了
实现步骤：
1、创建图类（显示图 邻接矩阵）
2、定义顶点数组 和 邻接矩阵
定义final N = 65535表示两顶点不可达
邻接矩阵赋值
3、创建图对象 测试输出图的邻接矩阵
4、记录已访问结点集合 创建一个类
创建三个数组already_arr[] pre_visited[] dis[]
1）记录各个是否已经全部访问的数组
2)记录每个顶点被访问前的前驱顶点
3）保存出发顶点与其他相怜顶点的边的距离，无边的话就是N
创建构造器（int lenth ，int index）
1）lenth：表示顶点的个数
2）index：出发顶点对应的下标
3）初始化dis[] Arrays.fi ll(dis,65535)
4)this.dis[index] = 0;
判断index顶点是否被访问过boolean类型方法
更新dis[] 更新出发顶点到index顶点的距离(int len,int index)
更新pre[] 更新pre这个顶点的前驱顶点为index顶点（int pre，int index）
返回出发顶点到index顶点的距离
5、迪杰斯特拉算法实现
创建VisitedVertex对象

6、更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点
根据遍历邻接矩阵的 行
1）更新j顶点的前驱为index顶点
2）更新出发顶点到j顶点的距离
7、在4中类添加方法
继续选择并返回新的访问顶点（注意：不是出发顶点了）
8、在dis算法中更新index顶点到周围顶点的的距离和前驱

package com.ldm.dijkstra;

import java.util.Arrays;

/**
 * @author 梁东明
 * 2022/9/14
 * 人生建议：看不懂的方法或者类记得CTRL + 点击 看看源码或者注解
 * 点击setting在Editor 的File and Code Templates 修改
 */
public class DijkstraAlgorithm {
    static char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
    public static void main(String[] args) {

        //邻接矩阵
        int[][] matrix = new int[vertex.length][vertex.length];
        final int N = 65535;// 表示不可以连接
        matrix[0]=new int[]{N, 5, 7, N, N, N, 2};
        matrix[1]=new int[]{5,N,N,9,N,N,3};
        matrix[2]=new int[]{7,N,N,N,8,N,N};
        matrix[3]=new int[]{N,9,N,N,N,4,N};
        matrix[4]=new int[]{N,N,8,N,N,5,4};
        matrix[5]=new int[]{N,N,N,4,5,N,6};
        matrix[6]=new int[]{2,3,N,N,4,6,N};
        //创建 Graph对象
        Graph graph = new Graph(vertex, matrix);
        //出发顶点对应的下标
        graph.dsj(6);
        //出发顶点对应的下标
        graph.showDijkstra(6);
    }
}



class Graph{
    private char[] vertex;  //顶点数组
    private int[][] matrix; //邻接矩阵
    private VisitedVertex vv; //已经访问的顶点的集合

    public Graph(char[] vertex, int[][] matrix) {
        this.vertex = vertex;
        this.matrix = matrix;
    }
    //显示图
    public void showGraph(){
        for (int[] links : matrix) {
            System.out.println(Arrays.toString(links));
        }
    }
    //显示Dijkstra算法的结果
    public void showDijkstra(int index){
        vv.show(index);
    }

    /**
     * 迪杰斯特拉算法实现
     *
     * @param index 出发顶点的下标
     */
    public void dsj(int index){
        vv = new VisitedVertex(vertex.length,index);
        update(index); //更新index下标的顶点到周围顶点的距离和前驱顶点
        //这里使用到贪心算法动态规划的思想
        for (int j = 0; j < vertex.length; j++) {
            index = vv.updateArr();//选择并返回新的访问结点
            update(index); //更新index下标的顶点到周围顶点的距离和前驱顶点
        }


    }

    /**
     * 更新index下标顶点的周围顶点的距离和周围顶点的前驱顶点，需要遍历图
     *
     * @param index index下标顶点
     */
    private void update(int index){

        int len; //index下标顶点的周围顶点的距离
        //根据遍历邻接矩阵的 matrix[index]行 用到图的广度遍历
        for (int j = 0; j < matrix[index].length; j++) {
            // len 含义是 : 出发顶点到index顶点的距离 + 从index顶点到j顶点的距离的和
            len = vv.getDis(index) + matrix[index][j];

            // 如果j顶点没有被访问过，并且 len 小于出发顶点到j顶点的距离，就需要更新
            if (!vv.in(j) && len < vv.getDis(j)){
                vv.updatePre(j,index);  //更新j这个顶点的前驱顶点为index
                vv.updateDis(j,len);    //更新j这个顶点到出发顶点的距离
            }
        }
        //for循环结束之后，记得要自己debug哦，不然单看代码不跟着流程走，你绝对会很懵逼
        //isVisited = {0,0,0,0,0,0,0}
        //pre_visited = {6,6,0,0,6,6,0}
        //dis = { 2,3,65535,65535,4,6,0}

    }

}

// 已访问顶点集合
class VisitedVertex {
    //记录各个顶点是否访问过 1表示访问过,0未访问,会动态更新
    public int[] isVisited;
    //保存当前顶点的前继顶点
    public int[] pre_visited;
    //记录出发顶点到其他所有顶点的距离,
    //比如G为出发顶点，就会记录G到其它顶点的距离，会动态更新，求的最短距离就会存放到dis
    public int[] dis;

    char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };

    /**构造器
     * 参观了顶点
     *
     * @param length 顶点的个数
     * @param index  出发点的下标
     */
    public VisitedVertex(int length, int index) {
        this.isVisited = new int[length];
        this.pre_visited = new int[length];
        this.dis = new int[length];
        //初始化dis数组
        Arrays.fill(dis,65535);
        //设置出发点被访问过
        this.isVisited[index] = 1;
        //出发顶点的访问距离是0
        this.dis[index] = 0;
    }

    /**
     * 判断index是否被访问过
     * @param index 下标
     * @return 如果访问过就返回ture，否则返回false
     */
    public boolean in(int index){
        return isVisited[index] == 1;
    }

    /**
     * 更新出发顶点到index顶点的距离
     *
     * @param len 传入的距离
     */
    public void updateDis(int index,int len){
        dis[index] = len;
    }

    /**
     * 更新 index顶点的前驱为顶点为pre顶点
     *
     * @param index 传入的顶点index
     * @param pre 传入的顶点pre
     */
    public void updatePre(int index,int pre){
        pre_visited[index] = pre;
    }

    /**
     * 返回出发点到index的顶点的距离
     *
     * @param index 指数
     */
    public int getDis(int index){
        //在第123行的方法中赋值
        return dis[index];
    }

    /**
     * 继续选择并返回新的访问顶点， 比如这里的G 完后，就是 A点作为新的访问顶点(注意不是出发顶点)
     *
     * @return int
     */
    public int updateArr(){
        int min = 65535, index = 0;
        //如果所有顶点没有被全部访问，for循环就不会退出
        for (int i = 0; i < isVisited.length; i++) {
            //当前顶点没有被访问,并且距离 小于min
            if ( isVisited[i] == 0 && dis[i] < min){
                //更新min的值
                min = dis[i];
                index = i ;
            }
        }
        //更新index为已访问过
        isVisited[index] = 1;
        return index;
    }
    //显示最后的结果
    //即将三个数组的情况输出
    public void show(int index) {

        System.out.println("==========================");
        //输出isVisited
        System.out.println("所有顶点是否全部被访问？");
        boolean[] Visited = new boolean[isVisited.length];

        for (int i = 0; i < isVisited.length; i++) {
            if ( isVisited[i] == 1){
                Visited[i] = true;
            }
        }
        for (boolean b : Visited) {
            System.out.print(b+" ");
        }
        System.out.println();
        System.out.println("\nA B C D E F G \n对应的前驱结点为：");
        //输出pre_visited
        for (int i : pre_visited) {
            System.out.print(vertex[i] + " ");
        }

        System.out.println("\n它们的边的权值分别为");
        //输出dis
        //统计最短路径
        int totalWeight = 0;
        for(int i : dis) {
            System.out.print(i + " ");
            totalWeight += i;
        }
        System.out.println();
        //为了好看最后的最短距离，我们处理
        char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
        int count = 0;
        for (int i : dis) {
            if (i != 65535) {
                System.out.print(vertex[count] + "("+i+") ");
            } else {
                System.out.println("N ");
            }
            count++;
        }
        System.out.println();
        System.out.println(vertex[index]+"到其他顶点的最短路径为：" + totalWeight);

    }
}
/*
实现步骤：
1、创建图类（显示图 邻接矩阵）
2、定义顶点数组  和 邻接矩阵
   定义final  N = 65535表示两顶点不可达
   邻接矩阵赋值
3、创建图对象  测试输出图的邻接矩阵
4、记录已访问结点集合 创建一个类
   创建三个数组already_arr[] pre_visited[] dis[]
   1）记录各个是否已经全部访问的数组
   2)记录每个顶点被访问前的前驱顶点
   3）保存出发顶点与其他相怜顶点的边的距离，无边的话就是N
   创建构造器（int lenth ，int index）
   1）lenth：表示顶点的个数
   2）index：出发顶点对应的下标
   3）初始化dis[] Arrays.fi ll(dis,65535)
   4)this.dis[index] = 0;
   判断index顶点是否被访问过boolean类型方法
   更新dis[] 更新出发顶点到index顶点的距离(int len,int index)
   更新pre[] 更新pre这个顶点的前驱顶点为index顶点（int pre，int    index）
   返回出发顶点到index顶点的距离
5、迪杰斯特拉算法实现
   创建VisitedVertex对象

6、更新index下标顶点到周围顶点的距离和周围顶点的前驱顶点
   根据遍历邻接矩阵的 行
   1）更新j顶点的前驱为index顶点
   2）更新出发顶点到j顶点的距离
7、在4中类添加方法
   继续选择并返回新的访问顶点（注意：不是出发顶点了）
8、在dis算法中更新index顶点到周围顶点的的距离和前驱


 */

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272

本次迪杰斯特拉算法算法 的教程出自韩顺平的数据结构与算法

数据结构和算法教程，哔哩哔哩详细教程
在 178-184p.

我在这里多嘴一下，老师的教程毕竟是三年前的了，所以代码上我做了很大的修改，几乎除了思想是一样的，很多都是不同的。我强烈建议你在学的过程中最好自己手敲一边代码，不要盲目的直接抄我的。你要是拿来应付作业就当我没说。
最后，认识一下，我是小白。努力成为一名合格的程序员。期待与你的下次相遇。