Programming Languages PartB Week2学习笔记——用Racket编写解释器

Datatype-Programming in Racket Without Structs

Racket没有提供类似ML的datatype来自定义one-of 类型，但由于它是动态类型语言，所以能够通过混合各种类型的值来实现这一点，不需要datatype

ML中用datatype来包装基础类型，就生成了同种类型的不同值，然后就能够储存在list中。这时候的构造器的pattern充当了分离的tags，用来识别某种基础类型。

但在Racket中，list不进行类型检查，本来就能够存储多种类型值，然后不依赖于pattern match区分每类型的值，而是通过每种值对应的tag检查函数来实现，例如number？ string？ pair？等。

（1）第一个例子：

Racket的实现

（2）第二个例子

下面是ML中的datatype递归定义和函数递归调用（在PartA中常见），但该函数只返回一个int值（ML返回值必须是同一类型），exp->int。但我们想要让他返回一个更通用的类型，exp->exp

因此需要一种新的方式来定义函数，始终返回一个Const of int（datatype定义的exp类型值）

在Racket中我们的做法是，使用一些辅助函数来定义数据类型构造器函数、实现类似pattern match的测试函数，实现数据extract函数

单引号加名称，是用来标记列表的symbol，例如下面的’Const，'Negate

整体实现思路其实类似，就是语法不同而已（借助辅助函数和函数传递，因为e可以是函数调用）

最后是关于Symbol的一些用法：

Datatype-Programming in Racket With Structs

Racket的结构体，语法如下：

struct定义时就会提供一些函数。结构体能够实现类似ML datatype的构造器的用法，但结构体定义的同时就已经同时提供了构造器、测试函数和extract函数。

例子：

另外，定义struct时用到了attribute，通过#: 加上关键词的形式使用。有点类似于java的注解，用来描述和定义struct的某些行为。例如transparent让struct values暴露出来，可以在REPL中print时显示内部的field值。如果没有transparent，struct内部field值必须通过函数调用之后才能看到

mutable可以为struct添加额外的函数，用于修改struct中fields的值（mcons就是一种预定义的可修改struct）

Advantages of Structs

方法比较，对比strut和我们自定义函数（使用list作为数据结构）的方式。struct不是自定义函数方式的语法糖（那当然，这并不是两种互通的语法，只是类似datatype的两种实现方式而已）

其核心区别在于，调用结构体的生成语句之后，得到的不是一个list，而是struct（可用于结构体定义时生成的各种相关函数）。结构体是一种不同于list的新的数据结构。

所以对比上述两种实现方式，用list来作为数据结构更容易出错。由于car，cdr能操作list，数据封装会被打破，list的标准库函数还会对函数调用造成混淆。并且对数据约束太弱，即使包含list包含一些无关数据，只要有’add标签就会被认为是正确值。

例子：下面Add和Multiply就是前面课程中介绍的函数方式

因此，struct相比之下具有多种优点

（1）更好的代码风格，更简洁的数据结构定义

（2）使用数据结构时（与list函数方法）同等的方便

（3）不容易误用数据结构

- 其一体现在存取函数不容易使用错误类型的数据（不容易因为只比较标签而使用错误类型的数据）
- 其二体现在测试函数不容易混淆（struct拥有专门的测试函数）
1
2

另外，struct在抽象方面具有更多的作用。

例如，一是在module system中定义abstract types，需要使用struct（list的库函数例如cons难以向用户隐藏，用户能随意制造改变module成员变量）。而通过struct隐藏module内部成员，然后向用户开放函数接口能实现抽象和封装。

二是contract system可以自己建立struct的比较（例如比较struct内部某个field是否属于某个类型），但对于list，因为list是相似和通用的，不会想strut那样（因为自己定义而）区别很大，所以很难为list建立比较所有情况的方法。

struct的特别在于他与其他特性和数据类型不同，每次定义struct都是生成一种新的数据类型。

比如 struct a ，和 struct b ，那么a 和b 也不一样，a? 判断b的话也会返回#f , 只有a才会返回#t。（跟C语言的结构体差不多）

Implementing Programming Languages

week2的作业是实现一个小型编程语言，编程语言的典型工作流

（1）根据code 文件中的具体语法（string），判断是否有明显的语法错误

（2）根据具体语法解析，创建抽象语法（抽象语法树，AST），判断是否有错误（例如如果需要type checking，是否有类型错误等）

（3）编译或者解释AST

下面是对解释器和编译器的介绍，解释器用语言A来对语言B的程序进行计算得到结果，而编译器用语言A来转换语言B成为语言C的程序（例如我们熟悉的C语言编译器将C语言转换为二进制程序），我们用来实现编译器或解释器的语言被称为metalanguage

事实上，现代语言两种方式都使用到了，通常混合使用，比较复杂。下面是java的例子：

Racket也混合了两种方式。

解释或编译是关于语言的执行方式，但不是语言的定义方式。从程序代码上是看不出来具体的执行方式的。

这里老师提到了很重要的一点，编译或解释不是衡量一个语言快慢的决定因素，（语言的快慢主要取决于语言的定义方式）不能说编译运行的语言就一定比解释运行的语言快，这是不可合理的。

不过某些时候，如果一个语言拥有“eval”函数（例如Racket的eval），可以用来承载并执行该语言的某些语句或者其他语言的语句，那么eval过程可能会慢一些。但这并不代表eval语句的执行一定是解释型的，它也可以用编译器实现。总而言之，就是语言的运行速度快慢和语言的执行方式关系不大

回到编程语言的工作流程中，课程中我们只是实现解释器的方式，使用PL A来实现PL B，可以skip parsing，直接用PL A来实现PL B的AST（直接将B的程序按照树状嵌入A中）。这个过程可以借助ML的构造器或者Racket的struct来实现。

这一步实际上就是将抽象AST转换到PL A的过程，实际上与PL B的语法没关系（因为skip parsing，跳过了对PL B进行语法解析生成AST的步骤，这一步骤似乎就不是课程所涵盖的内容了（也许是难度比较大？））

已经实现的例子：假设我们定义一种算术语言（Arithmetic Language），eval-exp就是解释器

What Your Interpreter Can and Cannot Assume

首先，需要明确的一点是，AST的子树也是AST。

我们编写的解释器可以假设AST是合法的程序（可能有错误的结果或者不可预见错误），但不能假设参数或者结果是正确的类型，所以需要检查（错误类型的情况，抛出异常）。因为子表达式递归计算有可能返回一个不正确的类型（例如需要const xx却返回了一个bool xx）。

还有一点需要注意，我们要检查的是表达式（expression）计算后的值（value）是否是某个类型（例如const xx）（详见本节最后的例子），而不是表达式本身是否是某个结构体或者什么其他类型。

同时，理论上，能被具体语法parsing检查出来的错误都应该算非法AST，例如 程序中使用 3 而不是 const 3作为某个输入（非本语言的输入结构）

解释器的结果一定是一个计算后的值value而不是表达式本身。这个value在大型语言中可能比较多样。

例子：解释器必须检查运行时的类型错误（这里的类型指的是PL B的类型，而不是PL A的类型），并给出错误信息

例如，下图定义的两段test代码都是合法的AST，但test2中使用了错误的类型（test2之所以合法是因为错误的不可预见但符合语法，if-then-else中有正确的出口const 7，和错误的出口bool #t，但两者在PL B中都是合法的表达式（符合语法）），因为错误分支中用了 bool b 而不是 const i ，multiply运行时理应判断两个参数是否都是const，所以这里是我们需要处理的错误。

比较上面的例子，下面这个例子中，non-test就不是一个合法的AST，因为const #t不符合我们定义的PL B的语法，这种错误是我们的解释器不需要处理的（解释器假设程序是合法的AST，如果AST不合法，应该直接终止解释器，而不是由我们定义抛出异常）。

这里的error是由PL A给出的，而不是我们在解释器中定义的。也就是说eval-exp这个解释器被终止了。

因此，（由于Racket是动态语言，我们的变量类型都是口头上说说而已），解释器应该真正去判断变量类型。

; 错误的解释器，没有对类型进行判断
(define (eval-exp-wrong e)
  (cond [(const? e) 
         e] 
        [(negate? e) 
         (const (- (const-int (eval-exp-wrong (negate-e1 e)))))]
        [(add? e) 
         (let ([i1 (const-int (eval-exp-wrong (add-e1 e)))]
               [i2 (const-int (eval-exp-wrong (add-e2 e)))])
           (const (+ i1 i2)))]
        [(multiply? e) 
         (let ([i1 (const-int (eval-exp-wrong (multiply-e1 e)))]
               [i2 (const-int (eval-exp-wrong (multiply-e2 e)))])
           (const (* i1 i2)))]
        [(bool? e) 
         e]
        [(eq-num? e) 
         (let ([i1 (const-int (eval-exp-wrong (eq-num-e1 e)))]
               [i2 (const-int (eval-exp-wrong (eq-num-e2 e)))])
           (bool (= i1 i2)))] ; creates (bool #t) or (bool #f)
        [(if-then-else? e)
         (if (bool-b (eval-exp-wrong (if-then-else-e1 e)))
             (eval-exp-wrong (if-then-else-e2 e))
             (eval-exp-wrong (if-then-else-e3 e)))]
        [#t (error "eval-exp expected an exp")] ; not strictly necessary but helps debugging
        ))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

; 添加对类型进行判断，错误时抛出异常
(define (eval-exp e)
  (cond [(const? e) 
         e] 
        [(negate? e) 
         (let ([v (eval-exp (negate-e1 e))])
           (if (const? v)
               (const (- (const-int v)))
               (error "negate applied to non-number")))]
        [(add? e) 
         (let ([v1 (eval-exp (add-e1 e))]
               [v2 (eval-exp (add-e2 e))])
           (if (and (const? v1) (const? v2))
               (const (+ (const-int v1) (const-int v2)))
               (error "add applied to non-number")))]
        [(multiply? e) 
         (let ([v1 (eval-exp (multiply-e1 e))]
               [v2 (eval-exp (multiply-e2 e))])
           (if (and (const? v1) (const? v2))
               (const (* (const-int v1) (const-int v2)))
               (error "multiply applied to non-number")))]
        [(bool? e) 
         e]
        [(eq-num? e) 
         (let ([v1 (eval-exp (eq-num-e1 e))]
               [v2 (eval-exp (eq-num-e2 e))])
           (if (and (const? v1) (const? v2))
               (bool (= (const-int v1) (const-int v2))) ; creates (bool #t) or (bool #f)
               (error "eq-num applied to non-number")))]
        [(if-then-else? e) 
         (let ([v-test (eval-exp (if-then-else-e1 e))])
           (if (bool? v-test)
               (if (bool-b v-test)
                   (eval-exp (if-then-else-e2 e))
                   (eval-exp (if-then-else-e3 e)))
               (error "if-then-else applied to non-boolean")))]
        [#t (error "eval-exp expected an exp")] ; not strictly necessary but helps debugging
        ))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

Implementing Variables and Environments

前面的例子都是一些常量以及他们的运算，本节需要实现变量

本节只讲原理，需要自己在作业中实现代码

environment是一个变量名（string）到值values的映射，在这里我们通过一个pair的list来实现。

environment作为参数传递到解释器的helper function中，也同时要传递到递归的subexpression中。因为他们都使用一套同样的environment。如果需要的变量不在environment中，解释器需要给出error。

当然，如果有let-expression，那么也会用到不同的environment。

由于Environment我们定义成一个list，其中包含由变量名和变量值构成的多个pair（类似于一种字典结构），所以week1中的练手作业正好就能派上用场，可见老师对课程的编排非常巧妙。

最后是一些关于作业的细节，正常情况下，我们将eval-under-env作为一个helper function（封装在eval-exp中），但作业中由于需要对eval-under-env进行评分，会在外部调用它，所以需要让它保持top-level

Implementing Closures

关于闭包的实现：

值得注意的是，我们实现的语言中（事实上不只是我们的语言，Racket这些语言也是一样），单独的函数定义不是一个值，而事实上闭包才是一个值（闭包必须包含函数定义和函数定义的环境）

我们调用function时的环境并不是函数定义的环境，所以我们定义一个closure结构，来保存函数的环境以便我们之后使用。

关于函数调用，实际上就是要注意call e1 e2中，e1和e2是表达式，不是值，所以要先求值。先用当前环境计算e1，e1计算后需要得到一个闭包c，再用当前环境计算e2得到值v。再使用闭包c的环境来计算闭包c中的函数体的值（所以不算其中的递归调用的话，这里的call一共计算三次，其中两次使用当前环境，一次使用闭包环境）：

Optional: Are Closures Efficient?

如果environment非常大，那么闭包可能会非常大

一种替代的方法是只在闭包中记录函数体中出现的free variables（指的是出现在function body 中，但不在function body 中定义或者shadowing的变量（也即是不包括函数参数和函数local变量））

例子：

解释器并不会每创建一次闭包就分析一次代码（不会每次创建闭包就在函数中寻找一次free variable），而是在全部计算之前，先计算每个函数的free variables存储起来。

这样通过时间换空间。

在将某个有闭包的语言编译成没有闭包的语言时，此时就没有解释器来存储environment了，因此必须显式地让编译后的函数携带额外的显式参数（extra explicit argument），这些被称为environment。

让程序自身携带environment，而不是我们之前让解释器携带environment的方式。

Racket Functions As “Macros” For Interpreted Language

回顾前面几节的内容

使用PL A在PL B中定义macro实际上就是使用PL A的函数来将某些具有PL B语言结构的表达式，生成一段PL B语言的“代码”，直接说可能有点抽象，看下面的例子就能理解了。

例子：使用的语言定义和解释器仍然是之前例子的代码（arithmetic language）

这里andalso e1 e2 就相当于是一种macro，调用函数andalso时就会先将其生成一段函数体定义好的PL B的“代码”，实现了宏展开。这个过程是在PL A中运行的，是在PL B程序运行（计算）之前，因此也符合macro的特点。

例2：

当这些函数被调用时，就会生成一个PL B的“代码“。

小结本章内容

本章主要是讲如何用Racket实现一种语言解释器。

编程语言的实现过程包含三大步骤：

其一是将某种语言B（PL B）的具体语法进行语法检测，排除一些明显的语法错误。然后解析（parsing），转化为抽象语法树（AST）。

其二是检查抽象语法树（AST）的错误，比如如果需要type checking就在这里检测。理论上这里应该得到合法的AST。

其三是通过编译器对程序进行编译（用一种语言A将语言B转换为另一种语言C的code）或通过解释器对程序进行解释（使用一种语言A计算语言B的值，然后返回计算结果）。编译其实应该叫做transfer，解释应该叫做evaluate。

本章就是围绕解释器来讲的，包括作业部分也是。

事实上，在课程中，我们假设第一步已经进行了（不是我们考虑的范畴），我们的解释器理论上应该获得一个合法的AST（否则终止解释器），合法的含义其实就是AST中的表述遵循语言PL B的语法，以课程的例子来表述，就是const 2是合法的，但const #f 就不合法（因为我们假定PL B的语法中const后必须跟上一个数值（至少是数值形式的量），如果跟上#f，那就是语法错误，应该在步骤一中排除，所以课程中老师说这种错误不需要我们来判断和处理，只要让Racket抛出异常就行了（终止编译器））。

运行时需要判断类型是否正确，这里的类型指的是PL B中各种参量的类型，因为我们用的PL A是Racket，是动态类型语言，没有设定每个结构体的参数或者返回值的类型（我们只是在假设他们有某种类型，但没有实际约束）。比如我们认为(Add e1 e2) 这个函数应该接受两个表达式，两个表达式计算之后的值都应该是const num（PL B的某种参量类型），但这只是假设，并没有实际约束。如果这两个表达式计算出来是bool b（PL B的某种参量类型）的类型也能够传入这个函数中（作为一段PL B的程序），也就是说这个程序没有语法错误（得到合法的AST），但我们知道，类型错误至少在运行时应该抛出异常，这个异常就应该由我们的解释器来抛出（而不是让Racket强行终止解释器），所以在编写时要尤为注意这些类型判断（一定不要假定程序不会出现类型错误）。

课程中用Racket的结构体struct来定义许多PL B的“语句”，实际上不是PL B真正的“语法”，而是一种抽象语法树的表示结构，例如，在Racket中用结构体(struct const num)来表示PL B的数字常量，似乎看起来const num就是PL B中定义数字常量的语句，但实际上PL B的语法可以是其他语句，比如类似C语言一样写成const int num。这样的不同是允许的，因为AST是抽象出来的（经过了步骤一的解析parsing，const int num能被解析成AST中的const num，再在PL A（这里也就是Racket）作为一个结构体被解释（计算））。

所以课程中（包括作业中），定义的PL B的AST的各种结构都是一系列Racket（PL A）的结构体，所谓PL B的程序（课程中指的是已经经过parsing的PL B 的AST）其实就是这些结构体的嵌套（因为AST是树状结构）得到的一个树数据结构，然后定义PL B的解释器就是对嵌套好的Racket结构体树进行判断（判断是什么结构体）、求值（根据每种结构体规定好的行为来进行计算）的一个Racket函数（比如课程中的eval-exp）。

所以本次作业表面上是编写一个新的编程语言及其解释器，看起来很难，但理解其实质，其实就是对Racket结构体定义和解释应用。当然，这个过程也确实能学到解释器的运行原理和编程语言的实现过程。再一次感叹这门课的精妙设计。

不过不得不说的是，这周的课程作业还是挺有难度的，有一部分原因是英文的作业文档表述不太清楚，看半天不知道到干什么。

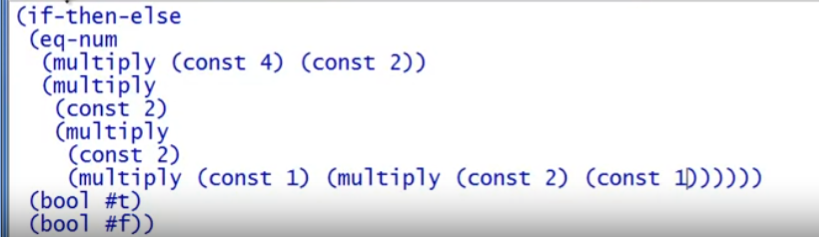
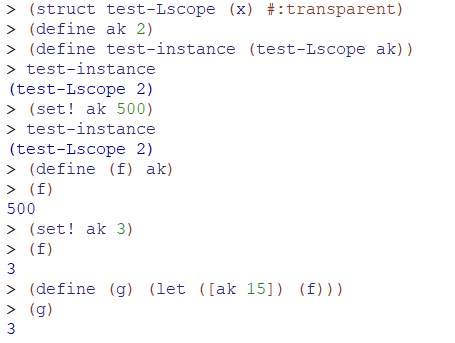
另外，必须认为作业中定义的语言PL B的各种参量是不能改变的（immutable），事实上也是如此，PL B中的所有表达式最终的出口都是int num，认为是一个常量。否则因为在struct中存储env实际上存储的是一个env copy，如果可以改变参量的值，那么真正env中的参量虽然不会被同名的local binding所覆盖，但有可能在后续的程序中被mutate（在函数定义之后、调用之前被修改，导致数值变化），这也是lexical scope的特点之一。因此假定PL B具备immutable的特性（env中不能有重复定义、不能修改某个已定义参量的值）简化了这个问题，让作业更简单。下面是例子：

关于使用Racket（PL A）对PL B实现宏定义，实际上就是定义一个Racket函数，把已有的一些结构体表达式和一些之前结构体定义重新组合（生成新的结构体实例），得到一个新的结构体表达式（PL B程序语句）。调用这个函数的过程就是宏展开过程。例如：ifaunit函数就是现在PL B的宏定义，e1 e2 e3是已有的结构体表达式，ifgreater、isaunit、int xx这些就是已有的结构体定义。因为宏展开过程是调用Racket函数的过程，所以实在eval-exp解释器运行之前，符合宏的定义。

题外话：学完Racket我写文档也莫名其妙用上了一大堆嵌套圆括号 (?)，笑死

这夸张的括号。