Matlab训练BP神经网络的一般步骤

  BP神经网络的算法原理可参考各种书籍（如《西瓜书》、《神经网络模型及其MATLAB仿真程序设计》等）或者博客（如 《零基础入门深度学习(3) - 神经网络和反向传播算法》等），本文不再赘述—— 本文力求使用Matlab工具箱函数快速搭建BP神经网络模型并用于实战！

1 网络创建、训练与仿真函数

1.1 网络创建：newff

  Matlab中使用 net=newff(PR,[S1,S2,...],{TF1,TF2,...},BTF,BLF,PF); 创建BP神经网络，各参数的含义如下：

  1. net：创建的BP网络（结构体）。
  2. PR：输入样本范围(R,2)，R为特征数。通常以minmax获取；
  3. [S1,S2,...]：隐层、输出层神经元数；
  4. [TF1,TF2,...]：激活（传输）函数（如tansig(logsig),purelin,poslin(ReLU)）；
  5. BTF：网络训练函数（default=traingdx）；
  6. BLF：网络学习函数（default=learngdm）；
  7. PF：网络性能函数（default=mse）。

1.2 网络训练：train

  Matlab中使用 [net,tr,Y,E,Pf,Af]=train(net,P,T,Pi,Ai,VV,TV); 训练网络，各参数的含义如下：
  1. net：训练后的BP网络；
  2. tr：训练记录，如训练次数net.epoch、训练误差性能net.perf等；
  3. Y：网络输出（S*Q即神经元数*样本数）；
  4. E：网络误差；
  5. Pf：最终输入延迟；
  6. Af：最终层延迟。
  7. net ：BP网络模型；
  8. P：输入（R*Q即特征数*样本数）；
  9. T：期望（或输出。S*Q，即神经元数*样本数）；
  10. Pi：初始输入延迟；
  11. Ai：初始层延迟；
  12. VV:验证集（结构体）；
  13. TV：测试集（结构体）。

1.3 仿真预测：sim

  Matlab中使用 [Y,Pf,Af,E,perf]=sim(net,P,Pi,Ai,T); 仿真预测，各参数含义如下：
  1. Y：拟合或预测值（S*Q）；
  2. Pf：最终输入延迟；
  3. Af：最终层延迟；
  4. E：网络误差（S*Q）；
  5. perf：网络性能。
  6. net：BP网络模型；
  7. P：拟合或预测输入；
  8. Pi：初始输入延迟；
  9. Ai：初始层延迟；
  10. T：拟合或预测期望。

1.4 网络保存及加载：save、load

  Matlab中使用 save 'E:\Matlab Codes\netName' net; 保存网络模型（网络训练完毕之后）；使用 load 'E:\Matlab Codes\netName' net; 加载网络模型（加载训练好的模型进行仿真预测）。

2 其他函数

2.1 数据归一化：mapminmax

2.1.1 归一化

  将X每行数据归一化至YMIN,YMAX之间：[Y,PS] = mapminmax(X,YMIN,YMAX)。其中，Y为归一化结果，PS为归一化信息（结构体）；YMIN,YMAX为每行的范围。也可将YMIN,YMAX构造为结构体FP（即FP.YMIN,FP.YMAX）。示例如下：

2.1.2 “应用”归一化

  将X按归一化信息PS（结构体）进行归一化：Y = mapminmax('apply',X,PS)。其中，Y为归一化结果；PS为归一化信息。此用法一般用来 按归一化训练数据方式归一化测试数据 。示例如下：

2.1.3 “反”归一化

  将Y按归一化信息PS（结构体）进行 反归一化 ：X = mapminmax(‘reverse’,Y,PS)。其中，X为反归一化结果；PS为归一化信息。此用法一般用来 反归一化网络拟合或预测结果 。示例如下：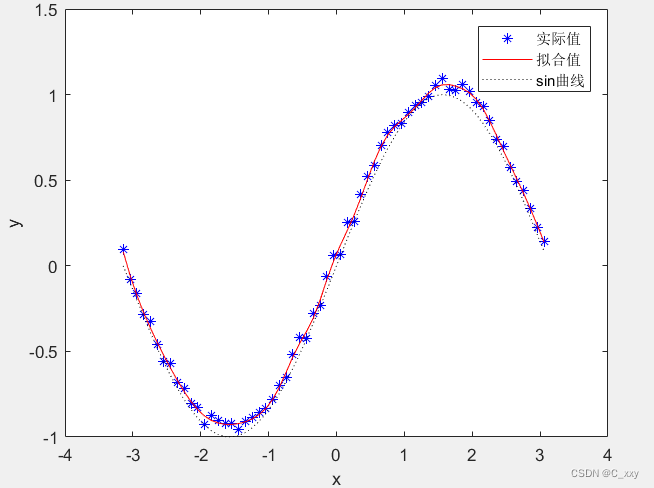

2.2 网络训练算法

  Matlab工具箱中的BP网络训练算法可按如下原则选取：
  ①中等网络（数百权值）、函数逼近、最大存储空间：LM算法（trainlm）；
  ②模式识别、（最小）存储空间较小：弹性BP算法（trainrp）；
  ③问题普适（拟合或分类）、大型网络、较小存储空间：变梯度SCG算法（trainscg）；
  ④某些问题有效、速度较慢、最小存储空间：变学习率算法（traingdx、traingda）。
  详情可参考：周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2005.

2.3 提高网络的泛化能力

2.3.1 贝叶斯归一化法：trainbr

  使用贝叶斯归一化法可 自动修正网络误差性能函数（自适应误差性能调整率） ，使网络获得较小的权值（W）和阈值（b），从而迫使网络响应趋于平滑，减小 “过适配” 。
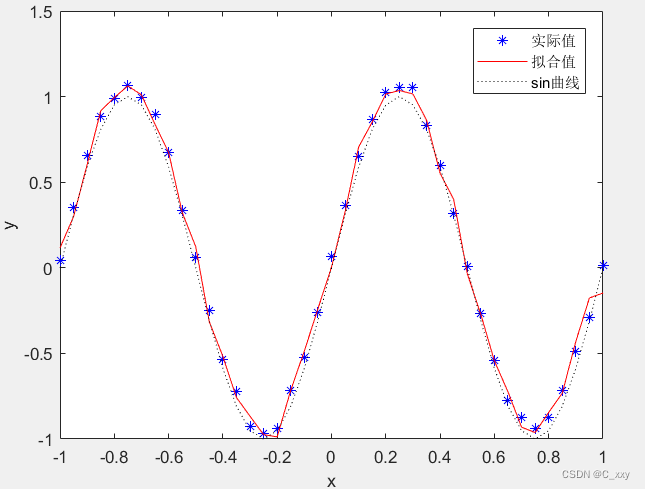
  贝叶斯归一化法使用方式为：net=newff(PR,[S1,S2,...],{TF1,TF2,...},trainbr,BLF,PF);，其收敛停机条件为：Maximum MU reached或者SSE（平方和误差）和SSW（平方和权值）基本不再变化。示例如下：

clc;clear;
% 样本数据
p_train=-pi:0.1:pi;
sinCurve=sin(p_train);
t_train=sin(p_train)+0.1*rand(size(p_train));
% 网络创建
net=newff(minmax(p_train),[15,1],{'tansig','purelin'},'traingd'); %最速下降BP算法
net.trainParam.show=50; %显示训练过程
net.trainParam.lr=0.01; %学习率
net.trainParam.epochs=1000; %最大迭代次数
net.trainParam.goal=1.0e-5; %性能目标
% 网络训练
[net,tr]=train(net,p_train,t_train);
% 网络仿真
t_sim=sim(net,p_train);
% 结果展示
plot(p_train,t_train,'b*',p_train,t_sim,'r-',p_train,sinCurve,'k:');
legend('实际值','拟合值','sin曲线');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

  拟合结果如下：

  使用 贝叶斯归一化法 训练网络，其拟合结果为：

  由图可知，后者的泛化能力更强，网络未出现过拟合现象。

2.3.2 提前终止法

  提前终止法的本质是 交叉验证 。将原始样本数据分成 训练集 和 验证集（或测试集），在训练初始阶段，验证集误差正常地减小，也即训练集的误差；而在网络开始出现“过适配”时，验证集误差开始增加，当其连续增加的次数达到指定的迭代次数时，训练便被终止。此时，网络返回具有最小验证集误差的权值和阈值（偏置）。
  提前终止法示例如下：

clc;clear;
% 样本数据
p_train=-1:0.05:1; %训练集
t_train=sin(2*pi*p_train)+0.1*rand(size(p_train));
sinCurve=sin(2*pi*p_train);
val.P=-0.975:0.05:0.975; %验证集
val.T=sin(2*pi*val.P)+0.1*rand(size(val.P));
% 网络创建
net=newff(minmax(p_train),[20,1],{'tansig','purelin'},'traingdx'); %学习率可变的动量BP算法
net.trainParam.show=25; %显示训练过程
net.trainParam.epochs=300; %最大迭代次数
% 网络训练
net=init(net);
[net,tr]=train(net,p_train,t_train,[],[],val);
% 网络仿真
t_sim=sim(net,p_train);
% 结果展示
plot(p_train,t_train,'b*',p_train,t_sim,'r-',p_train,sinCurve,'k:');
xlabel('x');ylabel('y')
legend('实际值','拟合值','sin曲线');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

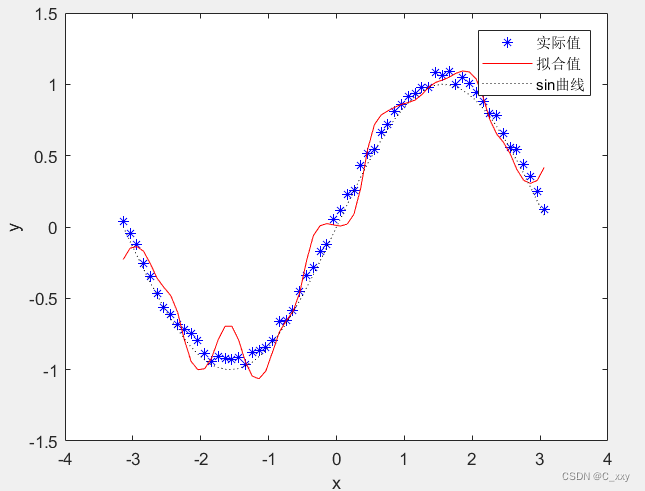
  结果如下：

  由图可知，网络可有效地避免“过适配”现象。

3 一个完整例子

clc;clear;

%%（1）训练测试数据（特征数R*样本数Q）
P_train=[-1,-1,2,2,4;0,5,0,5,7]; %R*Q
[PN_train,ps_input]=mapminmax(P_train,-1,1); %训练输入归一化
T_train=[-1,-1,1,1,-1]; %S*Q
[TN_train,ps_output]=mapminmax(T_train,-1,1);
P_test=[-1,-1,2,2,4;0,5,0,5,7];
PN_test=mapminmax('apply',P_test,ps_input); %测试输入归一化
T_test=[-1,-1,1,1,-1];

%%（2）构建网络并设置训练参数
%net=newff(PR,[S1,S2,...],{TF1,TF2,...},BTF,BLF,PF); %输入样本范围(R,2)；隐层、输出层神经元数；激活（传输）函数；网络训练函数（traingdx）；网络学习函数（learngdm）；性能函数（mse）
%1）TF：tansig(logsig),purelin,poslin(ReLU)；2）BTF：trainlm（中等网络函数逼近/存储空间大），traingdx、traingda（某些问题有效/速度慢），trainscg（大型网络通用），trainrp（模式识别），trainbr（贝叶斯归一化法提高泛化能力）
net=newff(minmax(PN_train),[5,1],{'tansig','purelin'},'traingdx');
net.trainParam.show=50; %显示训练过程
net.trainParam.lr=0.05; %学习率
net.trainParam.epochs=300; %最大迭代次数
net.trainParam.goal=1.0e-5; %性能目标

%%（3）网络训练
%[net,tr,Y,E,Pf,Af]=train(net,P,T,Pi,Ai,VV,TV); %1）网络，训练记录（epoch,perf），网络输出，网络误差，最终输入延迟，最终层延迟；2）网络，输入，期望，初始输入延迟，初始层延迟，确认样本结构（[]），测试样本结构（[]）
[net,tr]=train(net,PN_train,TN_train);
%save 'E:\Matlab Codes\netName' net; %保存网络

%%（4）训练结果：T=TF2(W2*TF1(W1*P+B1)+B2)
W1=net.IW{1,1}; %输入层到隐层权值
B1=net.b{1,1}; %隐层神经元偏置（阈值）
W2=net.LW{2,1}; %隐层到输出层权值
B2=net.b{2,1}; %输出层神经元偏置

%%（5）网络仿真预测
%[Y,Pf,Af,E,perf]=sim(net,P,Pi,Ai,T); %1）网络拟合/预测值，最终输入延迟，最终层延迟，网络误差，网络性能；2）网络，预测输入，初始输入延迟，初始层延迟，预测期望
%load 'E:\Matlab Codes\netName' net; %加载网络
TN_sim=sim(net,PN_test);
T_sim=mapminmax('reverse',TN_sim,ps_output); %测试结果反归一化

%%（6）结果展示
plotperform(tr); %训练性能
testNumber=length(T_test);
plot(1:testNumber,T_sim,'ro',1:testNumber,T_test,'b-');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

4 参考文献

  1. 周开利，康耀红.神经网络模型及其MATLAB仿真程序设计[M].北京：清华大学出版社，2005.
  2.丛爽.面向MATLAB工具箱的神经网络理论与应用[M].合肥：中国科学技术大学出版社，2009.